_____班；学号__________ 湖南省省级示范性高中……洞口三中数学测验试卷
姓名_____________ 高一第一学期直线与圆 阶段测试
撰稿： 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一、选择题（共50分）
★【题1】、已知两条直线
和
互相垂直，则
等于
（A）2 （B）1 （C）0 （D）
★【题2】、已知过点
和
的直线与直线
平行，则的值为
A 
B 
C 
D 
★【题3】、经过点
作圆
的切线，则切线的方程为：
A. 
B. 
C. 
D. 
★4、圆
与圆
外切，则m的值为：
A. 2 B. -5 C. 2或-5 D. 不确定
★5、圆
和
的公共弦所在直线方程为
A. x-2y=0 B. x+2y=0 C. 2x-y=0 D. 2x+y=0
★6、直线
与圆
没有公共点，则的取值范围是
A．
B．
C．
D．
★【题7】、圆
上的点到直线
的最大距离与最小距离的差是
A．36
B. 18 C. 
D. 
★【题8】设直线过点(0，a)，其斜率为1， 且与圆x2+y2=2相切，则a 的值为
A．± B．±2 B．±2 D．±4
★【题9】、已知两定点
，如果动点
满足
，则点的轨迹所包围的图形的面积等于( ） A 
（B）
（C）
（D）
★【题10】、如果直线L将圆：x2+y2-2x-4y=0平分且不通过第四象限,则直线L的斜率的取值范围是
A [0,2] B [0,1] C [0, ] D [0, )
二、填空题（共25分）
★【题11】已知两条直线
若
，则
★【题12】已知圆
－4
－4＋
＝0的圆心是点P，则点P到直线－
－1＝0的距离是
★【题13】圆
是以
为半径的球
的小圆，若圆的面积
和球的表面积
的比为
，则圆心到球心的距离与球半径的比
____
★【题14】、若直线x+y=k与曲线y=恰有一个公共点,则k的取值范围是____
★【题15】、过点（1，）的直线L将圆(x－2)2＋y2＝4分成两段弧，当劣弧所对的圆心角最小时，直线L的斜率k＝ ．
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
★答案：
★11．__________________; ★12题 :_____________;
★13题:__________________; ★14题:__________________; ★15题:________________
三、解答题（共75分）
★16题、（1）、若半径为1的圆分别与轴的正半轴和射线
相切，求出这个圆的方程。
(2)、已知点
和圆
，求一束光线从点A经x轴反射到圆周C的最短
路程。
★17题、(Ⅰ)、已知圆C的圆心坐标是(-1,3),且圆C与直线x+y-3=0相交于P,Q两点,又OP⊥OQ,O是坐标原点,求圆C的方程.
（Ⅱ）、已知⊙C满足：（1）、截y轴所得的弦长为2；（2）被x轴分成两段圆弧，其弧长之比为3：1；（3）、圆心到直线L:x-2y=0的距离为，求此圆的方程。
★ 【题18】、（1）已知直线
与圆
相切，求出
的值。
(2)、某条直线过点
，被圆
截得的弦长为8，求此弦所在的直线方程。
★【例题19】已知直线过点P（-1，2）,且与以点A（-2，-3）、B（3，0）为端点的线段相交，求出直线L的斜率的取值范围是多少？
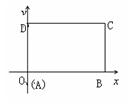※★【题20】在平面直角坐标系中，已知矩形
的长为２，宽为１，
、
边分别在轴、轴的正半轴上，
点与坐标原点重合（如图所示）．将矩形折叠，使点落在线段
上．若折痕所在直线的斜率为
，试写出折痕所在直线的方程。
★【题21】、已知圆C：（x-1)2+(y-2)2= 25，直线L：(2m+1)x+(m+1)y-7m-4=0；①证明；不论m取什么值，直线L恒与圆C相交于两点；②求直线被圆C所截得的弦长最小时，直线L的方程是什么？
参考答案
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | C | C | B | A | C | B | C | A |
★一、选择题和填空题：
★11．2 ★12题 : 
★13题: 1 : 3_
★14题: -1≤k<1或k= ★15题:
★16题、(1)、解：若半径为1的圆分别与轴的正半轴和射线相切，则圆心在直线y=
x上，且圆心的横坐标为1，所以纵坐标为，这个圆的方程为
。
★17题、（Ⅰ）解：（1）设而不求思想的应用，（2）OP⊥OQ转化为x1x2+y1y2=0，从而可求得r2=13
（3）、所求的圆的方程为
（Ⅱ）、解：
或
★18题、（1）、解：圆的方程可化为
，所以圆心坐标为（1，0），半径为1，由已知可得
，所以的值为－18或8。
★题19 k≥5,或k≤
★题20：（Ⅰ）(
i ) 当
时,此时A点与D点重合,
折痕所在的直线方程
，( ii ) 当
时，设A点落在线段上的点
， 
，则直线
的斜率
，∵
∴
，∴
，∴
；又∵折痕所在的直线与
的交点坐标（线段的中点）；为
，∴折痕所在的直线方程
，即
，由( i ) ( ii )得折痕所在的直线方程为：
★题21、（1）证明直线L恒过定点（3，1）；（2）、直线L的方程为：2x-y-5=0