_____班；姓名_____________ 湖南省省级示范性高中……洞口三中数学月考测验试卷
学号__________ 高一第二学期月考测试题
撰稿： 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一:选择题(50分):
1、从一批产品中取出三件产品，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品至少有一件是次品”，则下列结论正确的是（ ）
A. A与C互斥 B. 任何两个均互斥
C. B与C互斥 D. 任何两个均不互斥
2、若考试成绩y（分）与复习时间x（小时）的回归直线是
，下列判断正确的是( ):
A、复习时间为10小时，成绩一定在65分 B、复习时间为10小时，成绩在65分左右
C、复习时间为10小时，成绩在65分以上 D、复习时间为10小时，成绩在65分以下
3、设
，则有（ ）
A、
B、
C、
D、
4、若函数
对任意实数x都有
，那么，
的值为（ ）
A、—2 B、2 C、±2 D、4
5、已知某矩形
其中
;则P点出现的概率( )
6、△ABC中，如果
则△ABC的形状是（ ）
A、等边三角形 B、直角三角形 C、等腰三角形 D、等腰直角三角形
7、若
则
（ ）
A、
B、
C、
D、
8、已知
则
的取值范围是（ ）
A、[6，10] B、
C、
D、[2，6]
9、将一枚骰子抛掷两次，若先后出现的点数分别为b、c，则方程
有实根的概率为（ ）
A、
B、
C、
D、
10、已知O是△ABC所在平面内的一点，满足
，则O点（ ）
A、在AB边的高线所在直线上 B、在∠A的平分线所在的直线上
C、在AB边中线所在的直线上 D、以上都不对
二:填空题(25分):
11.某城市有500所学校，其中大学10所，中学200所，小学290所.现在取50所学校作为一个样本进行一项调查，用分层抽样进行抽样,应该选取大学________所，中学________所，小学________所.
12、已知
且
则
___________
13、在大小相同的6个球中，4个是红球，若从中任意选2个，求所选的2个球至少有一个是
红球的概率____
14、已知
，
，
，
，且
∥
，则求
的值._______
15、已知
与
的夹角为
，且
则与
的夹角的余弦值为______
三：解答题:
16题(4+4+3+3=14分)．函数
一段图象如图所示。
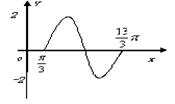⑴、求出函数
的解析式； (2)函数的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到?
(3)、求出的单调递增区间；
(4)、指出当取得最小值时
的集合．
17（12分）、盒中有6只灯泡，其中2只次品，4只正品，有放回的从中任抽2次，每次抽取1只，试求下列事件的概率： （1）第1次抽到的是次品； （2）抽到的2次中，正品、次品各一次
18（10分）．为了参加奥运会，对自行车运动员甲、乙两人在相同的条件下进行了6次测试，测得他们的最大速度的数据如表所示：
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
请判断：谁参加这项重大比赛更合适，并阐述理由。
19（12分）. 设
,
是两个不共线的非零向量，如果
，
，
.
（1）、试确定实数
的值，使的取值满足向量
与向量
共线；
（2）、证明：A、B、D三点共线．
20．（Ｉ）（8分）甲乙两人约定在6时到7时在某地会面，并约定先到者等候另一人一刻钟，过时
即可离去，求两人能会面的概率？
（Ⅱ）（9分） 在120个零件中，一级品24个，二级品36个，三级品60个，从中抽取一个容量
为20的一个样本，求 ① 每个个体被抽到的概率，
② 若有简单随机抽样方法抽取时，其中个体α第15次被抽到的的概率，
③ 若用分层抽抽样样方法抽取时其中一级品中的每个个体被抽到的概率.
21（10分）、是否存在常数
，使得函数
在闭区间[0，
]上的最大值是1？
若存在，求出对应的值；若不存在，试说明理由.
参考答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | C | C | A | B | A | B | D | A |
11题、1 20
29； 12题、-3； 13题：；
14题、；
15题：
16．解：（1）、 
（2）单调递增区间为 
（3）当 
时 
17、第1次抽到的是次品的概率为
，抽到的2次中，正品、次品各一次的概率为
18．
； 
S甲=
， S乙=
；
，S甲＞S乙；乙参加更合适
19. 解：
若向量与向量共线; 则存在实数
使得 
成立
即
则 
解得 
2） 证明：∵ 
;又∵
∴ 
; ∴
; 又
有公共点
,∴A、B、D三点共线
20．（Ｉ）解：设“两人能会面”为事件
，以 x和y分别表示甲、乙两人到达约会地点的时间，则两人能够会面的充
要条件为： 
在平面上建立如图所示的坐标系，则
的所有可能的结果是边长为60的正方形,而可能会面的时间由图中阴影部分所表示，由几何概型知，
答：两人能会面的概率
.
（Ⅱ）解：① 因为总体个数为120，样本容量为20，则每个个体被抽到的概率P
=
=
② 因为总体个数为120，则体α第15次被抽到的的概率P
=
③ 用分层抽样方法：按比例=分别在一级品、二级品、三级品中抽取24×=4个，36×=6个，60×=10，所以一级品中的每个个体被抽到的概率为P
=
=.
21、解： 
=
当 
时，
; (1)若
， 
(2)若
，
(3)若
，
综上述知，存在
符合题设.