算法初步单元测试题
一、选择题
1．根据下面的伪代码，写出执行结果. （ ）
sum←0
For x=1 to 10
sum←sum+x
If sum>10 then
End for
End if
End for
A.10 B.15 C.45 D.55
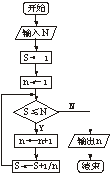
2．下面的流程图表示的算法执行的结果是 （ ）
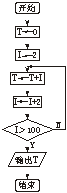
A.5050 B.2550 C.2450 D.2500
3．以下求方程x5+x3+x2－1＝0在［0，1］之间近似根的算法是 （ ）
x1←0
x2←1
x←（x1+x2）/2
c←0.00001
While x2－x1>c
If x5+x3+x2－1>0 then
x2←x
Else
x1←x
End if
x=（x1+x2）/2
End while
Print x
A.辗转相除法 B.二分法 C.更相减损术 D.秦九韶算法
4．解决某一问题而设计的 有限的步骤称为算法. （ ）
A.确定的 B.有效的 C.连续的 D.无穷的
5．用秦九韶算法求多项式f（x）=12+35x－8x2+79x3+6x4+5x5+3x6在x=－4的值时，v4的值为（ ）
A.－57 B.220 C.－845 D.3392
6．如果有下列这段伪代码，那么将执行多少次循环 （ ）
sum←0
For x=1 to 10
sum←sum+x
If sum>10 then
Exit For
End if
Next
A.4次 B.5次 C.7次 D.10次
7．下面的伪代码输出的结果S为 （ ）
I←1
While I<8
I←I+2
S←2I+3
End while
Print S
A.17 B.19 C.21 D.23
8．流程图中表示处理框的是 （ ）
A.矩形框 B.菱形框 C.圆形框 D.椭圆形框
9．下面伪代码表示的算法中，最后一次输出的I的值是 （ ）
For I=2 to 13 Step 3
Print I
Next I
Print “I=”，I
A.5 B.8 C.11 D.14
10．设学生的考试成绩为G，则下面的代码的算法目的是 （ ）
n←0
m←0
While n<50
Read G
If G<60 then m←m+1
n←n+1
End while
Print m
A.计算50个学生的平均成绩 B.计算50个学生中不及格的人数
C.计算50个学生中及格的人数 D.计算50个学生的总成绩
第Ⅱ卷
一、选择题(10×5＝50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(6×4＝24分)
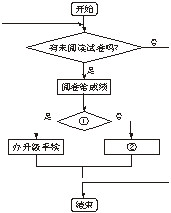
11．期末考试，教师阅卷评分，并检查每个学生成绩，如及格则作“升级”处理，不及格作“留级”处理.将下面的流程图补充完整.
12．说出下列算法的结果.
Read a，b，c
If a2+b2=c2 then
Print“是直角三角形！”
Else
Print“非直角三角形！”
End if
运行时输入3、4、5
运行结果为输出： .
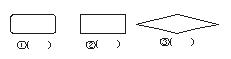13．已知流程图符号，写出对应名称.
（1） ；（2） ；（3） .
14．算法的5大特征分别是：（1）有0到多个输入；（2） ；（3）可行性；
（4）有限性；（5） .
15．描述算法的方法通常有：
（1）自然语言；（2） ；（3）伪代码.
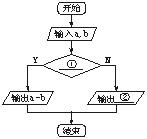
16．根据题意，完成流程图填空：
输入两个数，输出这两个数差的绝对值.
（1） ；（2）
三、解答题(12＋12＋12＋13＋13＋14＝76分)
17．（1）说出下列伪代码表示的算法目的.
Begin
S←1
I←3
While S≤10000
S←S×I
I←I+2
End while
Print I
End
（2）根据伪代码，写出执行结果.
算法开始
x←4；
y←8；
If x<y then
x←x+3；
End if
x←x－1；
输出x的值；
算法结束
18．输入一学生成绩，评定其等级.方法是：90～100分为“优秀”，80～89分为“良好”，60～79分为“及格”，60分以下为“不合格”.写出其算法的伪代码并画出流程图.
19．随着人的年龄的增加，成年人的肺活量会逐渐减少，假如我们用V表示人的肺活量（单位为L），用h表示人的身高（单位为英寸），a表示年龄，则这几个量近似的满足关系式：V=0.104h－0.018a－2.69.请设计算法流程图，输入身高、年龄，输出肺活量.
20．一块橡皮1元钱，一枝笔2元钱，问100元钱能买橡皮和笔各多少？
数学模型：设能买橡皮X块，笔Y枝，则X+2Y= 100.求此方程的正整数解.
设计一个求此问题的算法，画出流程图并用伪代码表示.
21．通过计算机验证：任意给定一个自然数N，一定存在自然数n，使1+1/2+1/3+…+1/n>N.
写出流程图和伪代码.
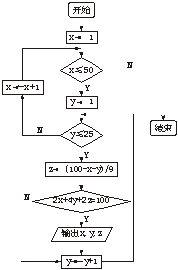
22．相传在远古时代有一片森林，栖息着3种动物，凤凰、麒麟和九头鸟.凤凰有1只头2只脚，麒麟是1只头4只脚，九头鸟有9只头2只脚.它们这3种动物的头加起来一共是100只，脚加起来也正好是100只，问森林中各生活着多少只凤凰、麒麟和九头鸟？写出算法、流程图及伪代码.
算法初步单元练习题答案
一、选择题(10×5＝50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | B | A | B | B | C | A | D | B |
二、填空题(6×4＝24分)
11．①及格 ②办留级手续 12．是直角三角形! 13．起止框 处理框 判断框
14．确切性 有1个或多个输出 15．流程图 16．①a>b ②b－a
三、解答题(12＋12＋12＋13＋13＋14＝76分)
17．（1）寻找最小的正整数I，使1×3×5×7×…×I>10000. （2）6.
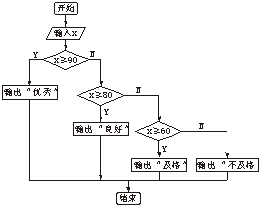
18．输入一学生成绩，评定其等级.方法是：90～100分为“优秀”，80～89分为“良好”，60～79分为“及格”，60分以下为“不合格”.写出其算法的伪代码并画出流程图.
解：可以用If…then…Else的嵌套完成.
伪代码如下：
Read x
If x≥90 then
Print“优秀”
Else If x≥80 then
Print“良好”
Else If x≥60 then
Print“及格”
Else
Print“不及格”
End If
流程图：
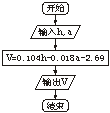
19．随着人的年龄的增加，成年人的肺活量会逐渐减少，假如我们用V表示人的肺活量（单位为L），用h表示人的身高（单位为英寸），a表示年龄，则这几个量近似的满足关系式：V=0.104h－0.018a－2.69.请设计算法流程图，输入身高、年龄，输出肺活量.
解：
20．一块橡皮1元钱，一枝笔2元钱，问100元钱能买橡皮和笔各多少？
数学模型：设能买橡皮X块，笔Y枝，则X+2Y= 100.求此方程的正整数解.
设计一个求此问题的算法，画出流程图并用伪代码表示.
解：伪代码和流程图如下：
Begin
For Y from 1 to 49
X←100－2Y
Print X，Y
End for
End
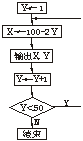
21．通过计算机验证：任意给定一个自然数N，一定存在自然数n，使1+1/2+1/3+…+1/n>N.
写出流程图和伪代码.
解：伪代码：
Read N
S←1
n←1
While S≤N
n←n+1
S←S+1/n
End while
Print n
End
流程图：
22．相传在远古时代有一片森林，栖息着3种动物，凤凰、麒麟和九头鸟.凤凰有1只头2只脚，麒麟是1只头4只脚，九头鸟有9只头2只脚.它们这3种动物的头加起来一共是100只，脚加起来也正好是100只，问森林中各生活着多少只凤凰、麒麟和九头鸟？写出算法、流程图及伪代码.
解：假设凤凰的只数为x，麒麟的只数为y，九头鸟的只数为z，那么，
（1）凤凰的只数x可能的取值为1～50，如果用伪代码表示，就应该如下：
For x=1 To 50 Step 1
（2）麒麟的只数y可能的取值为1～25，如果用伪代码表示，就应该如下：
For y = 1 To 25 Step 1
（3）如果知道了凤凰和麒麟的只数后，那么九头鸟的只数就应该如下：
z=（100－x－y）/9.
如何考虑x、y、z三个变量之间的关系？
当凤凰x=1时（只在开始时），变量麒麟y的取值可以从1～25，让变量y从1开始取值（例如：y的值为1）；
通过（100－x－y）/9表达式，计算出z的值；
完成上述步骤后，x、y、z三个变量都取到了自己相应的值，但是这三个值是否是正确的解呢？我们必须通过以下的两个条件来判断：
x+y+9×z=100 And 2×x+4×y+2×z=100.
如果全部满足，就输出x、y、z的值，如果不满足，就让y值加1，然后重复步骤（2）到步骤（4），直至y的取值超过25；
然后让x的取值加1后，重复步骤（1）到步骤（5）的操作，直至x的取值超过50为止，退出算法.
流程图和伪代码如下：
For x from 1 to 50
For y from 1 to 25
z←（100－x－y）/9
If 2x+4y+2z=100 then
Print I，J，K
End for
End for
