高一数学第一学期期中考试试题
高一数学
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下列集合中, 不是方程![]() 的解集的集合是
( )
的解集的集合是
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.已知集合A=R,B=R+,若![]() 是从集合A到B的一个映射,则B 中的元素3对应A中对应的元素为 ( )
是从集合A到B的一个映射,则B 中的元素3对应A中对应的元素为 ( )
A.![]() B.
B.
3. 已知![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 函数![]() ( )
( )
A.是奇函数但不是偶函数 B.是偶函数但不是奇函数
C.既是奇函数也是偶函数 D.既不是奇函数也不是偶函数
5.根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为 ( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
A. (-1,0) B. (0,1) C. (1,2) D. (2,3)
6. 三个数![]() 的大小关系为
( )
的大小关系为
( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
7. 函数![]() 的定义域是
( )
的定义域是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知全集![]() ,若非空集合
,若非空集合![]() ,则实数
,则实数![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、如果函数![]() 在区间
在区间![]() 上是减少的,那么实数
上是减少的,那么实数![]() 的取值范围
的取值范围
是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10.已知![]() 是偶函数,它在
是偶函数,它在![]() 上是减函数,
上是减函数,![]() ,若
,若![]() ,
,
则![]() 的取值范围是
( )
的取值范围是
( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答卷相应位置上.
11. 设全集![]() ,集合
,集合![]() ,
,![]() 。
。
12![]() 已知幂函数
已知幂函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]() =_________________
_。
=_________________
_。
13.设函数![]() , 则满足
, 则满足![]() =
=![]() 的x的值为
。
的x的值为
。
14. 对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)·f(x2); ② f(x1·x2)=f(x1)+f(x2) ③![]() >0;
>0;
④![]() .
.
当f(x)=lgx时,上述结论中正确结论的序号是 .
三、解答题:本大题共7小题,每题10分,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
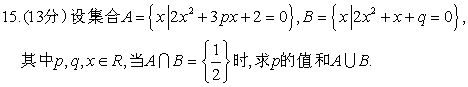
16.(1)计算![]() 的值. (7分)
的值. (7分)
(2)计算![]() 的值.(6分)
的值.(6分)
17.(14分)已知函数f(x)=x+![]() ,且f(1)=2.
,且f(1)=2.
(1)求m;
(2)判断f(x)的奇偶性;
(3)函数f(x)在(1,+∞)上是增函数还是减函数?并证明.
18.(12分)已知一次函数![]() 的图象过点
的图象过点![]() 和
和![]() .
.
(1)求该函数的解析式.
(2)若![]() , 求
, 求![]() 的值域.
的值域.
19、(14分)某商品在近30天内,每件的销售价格P(元)与时间t(天)的函数关系是:
![]() ,该商品的日销售量Q(件)与时间(天)的函数关系是Q= -t+40 (0<t≤30,
,该商品的日销售量Q(件)与时间(天)的函数关系是Q= -t+40 (0<t≤30,![]() ),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
20.(14分)定义在(-1,1)上的函数![]() 满足:
满足:
①对任意x,![]() (-1,1)都有
(-1,1)都有![]() ;
;
②当![]() (-1,0)时,
(-1,0)时,![]() .
.
(Ⅰ)判断![]() 在(-1,1)上的奇偶性,并说明理由;
在(-1,1)上的奇偶性,并说明理由;
(Ⅱ)判断函数![]() 在(0,1)上的单调性,并说明理由;
在(0,1)上的单调性,并说明理由;
高一数学期中试答案
一、选择题:BCADC DBDAA
二、填空题:11. ![]() ; 12. 3 ; 13.
; 12. 3 ; 13. ![]() ; 14. ②③
; 14. ②③
三、解答题:
15. 解:![]() 2分
2分
![]() 6分
6分
![]() 9分
9分
![]() 13分
13分
16.解:(1)原式![]() (3分)
(3分)
![]() (7分)
(7分)
(2)原式![]() (10分)
(10分)
![]() (13分)
(13分)
17.解:(1)f(1)=1+m=2,m=1. (2分)
(2)f(x)=x+![]() ,f(-x)=-x-
,f(-x)=-x-![]() =-f(x),∴f(x)是奇函数.(6分)
=-f(x),∴f(x)是奇函数.(6分)
(3)设x1、x2是(1,+∞)上的任意两个实数,且x1<x2,则
f(x1)-f(x2)=x1+![]() -(x2+
-(x2+![]() )=x1-x2+(
)=x1-x2+(![]() -
-![]() )
)
=x1-x2-![]() =(x1-x2)
=(x1-x2)![]() . (10分)
. (10分)
当1<x1<x2时,x1x2>1,x1x2-1>0,从而f(x1)-f(x2)<0,
即f(x1)<f(x2).
∴函数f(x)=![]() +x在(1,+∞)上为增函数.(14分)
+x在(1,+∞)上为增函数.(14分)
18.解:(1)由已知得![]() ,
,![]() …5分
…5分
(2)![]()
![]()
![]() …9分
…9分
![]()
![]()
![]() …12分
…12分
19.解:设这种商品日销售额为![]() 元。 则
元。 则![]() ,………1分
,………1分
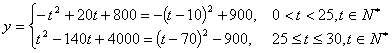 ………7分
………7分
当![]() 时,
时,![]() ,
,![]() (元);………9分
(元);………9分
当![]() 时,
时,![]() (元)。………11分
(元)。………11分
![]() 所以
所以![]() (元),故所秋日销售金额的最大值为1125元,且在最近30天中的第25天日销售金额最大。………13分
(元),故所秋日销售金额的最大值为1125元,且在最近30天中的第25天日销售金额最大。………13分
![]()
20.(Ⅰ)证明:令![]() .
……………2分
.
……………2分
令y=-x,则![]()
![]() 在(-1,1)上是奇函数. 6分(Ⅱ)证明:设
在(-1,1)上是奇函数. 6分(Ⅱ)证明:设![]() ,则
,则![]() ,8分
,8分
而![]() ,
,![]() . ……………………10分
. ……………………10分
![]() .即 当
.即 当![]() 时,
时,![]() .
.
∴ f(x)在(0,1)上单调递减. ………………………14分