高一数学第一学期期中试卷
高一数学
一、选择题：本大题共有6小题，每小题5分，共30分．
1．若集合
，则M∩P=
A．
B．
C．
D．
2．若函数
在R上为单调减函数，那么实数
的取值范围是
A. 
B. 
C. 
D.
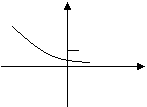3. 已知函数y=
图象如图所示，则实数、
的范围是 
|
>1, 0<<1
B. 0<<1, 0<<1
1
C. >1, >0
D. 0<<1, <0
4．已知偶函数y= f(x)有四个零点，则方程f(x)=0的所有实数根之和为
A．4 B．2 C．1 D．0
5．函数
的单调递增区间为
A．（－∞，1） B．（2，+∞） C．（－∞，
） D．（，+∞）
6．根据表格中的数据，可以断定方程
的一个根所在的区间是
|
| －1 | 0 | 1 | 2 | 3 |
|
| 0．37 | 1 | 2．72 | 7．39 | 20．09 |
|
| 1 | 2 | 3 | 4 | 5 |
A．（－1，0） B．（0，1） C．（1，2） D．（2，3）
二、填空题：本大题共10小题，每小题5分，共50分．
7、函数y=
的定义域为_____________。
8．给定集合A、B，定义一种新运算：
.已知
，
，用列举法写出
.
9．方程2x=2－x的实数解有________个.
10．计算机成本不断降低，若每隔3年计算机价格降低
，现在价格为8100元的计算机，9年后的价格可降为___________元.
11．已知
，若
，则
12. 若方程
的解为，且
，则
=_______.
13.函数
是
上的奇函数，且当
时，
，那么当
时，
。
14.函数
，
。若的值有正有负，则实数的取值范围是
。
15．下列几个命题：
①方程
的有一个正实根，一个负实根，则
；
②函数
是偶函数，但不是奇函数；
③函数
的值域是
，则函数
的值域为
；
④ 设函数
定义域为R，则函数
与
的图象关于轴对称；
⑤一条曲线
和直线
的公共点个数是
，则的值不可能是1.
其中正确的有_______________.
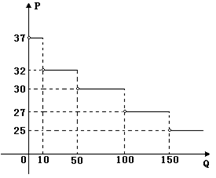
16．某批发商批发某种商品的单价P（单位：元/千克）
与一次性批发数量Q（单位：千克）之间函数的图像
如图2，一零售商仅有现金2700元，他最多可购买这
种商品 千克（不考虑运输费等其他费用）．
|
|
……………装……………订……………线……………内……………请……………不……………要……………答……………题……………答题纸
成绩
一、选择题：（每小题5分，共30分．）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 得分 |
| 答案 |
|
|
|
|
|
|
二、填空题：（每小题5分，共50分．）
7.____ ___; 8.___ ____; 9.____ ___; 10
11.____ 12.____ _ _; 13.___ ____; 14._____ __
15.___ _ ___,16.___ _ ___,
三、解答题；（共6题，80分）
17．求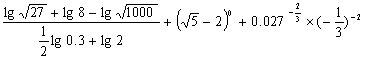
的值 （12分）
18、
（1）求的值及
、
（2）设全集
，求
；
（3）写出的所有子集；
（14分）
19.(1)应用单调性定义证明函数
在
上的单调性;
(2)求函数
在[1,2]上的值域.
（14分）
20．已知函数f(x)=-x+log2
.
(1)求f(
)+f(-)的值;
(2)当x∈
(其中a∈(-1, 1), 且a为常数)时, f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由.
（14分）
21.有甲、乙两种商品，经营销售这两种商品所能获得的利润依次是P和Q（万元），它们与投入的资金
（万元）的关系满足公式P=
，Q=
，现将3万元资金投入经营甲、乙两种商品，设投入乙的资金为x万元，获得的总利润为y（万元）.
（1）用x表示y,并指出函数的定义城;
（2）x为何值时,y有最大值,并求出这个最大值. （12分）
22．设函数
是定义在
上的函数，并且满足下面三个条件：（1）对正数x、y都有
；（2）当
时，
；（3）
（I）求
和
的值；
（II）如果不等式
成立，求x的取值范围．
（III）如果存在正数k，使不等式
有解，求正数
的取值范围．（14分）
答案
一、选择题： C B D D A C
二、填空题：
7、
8、{0，3} 9、2400
10、 2
11、－1或2 12、2
13.
14.`
15、①⑤ 16、90
三、解答题：
17题：解：∵原式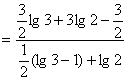
+1+
+1+100
+101=104
18.(1).a=-5，A={1/2,2}B={-5,2}
(2).={1/2，2，-5}
(3).空集、{1/2}、{-5}、{1/2，-5}
19、解: (1)略;
(2) 
令
则
，
由（1）可知，函数
在
上单调递增，
故
，
所以函数在[1,2]上的值域为
.
20 解:（1）易求f(x)的定义域是(-1, 1),
∵f(-x)=-(-x) +log2
=-(-x+log2)=- f(x)
∴f(x)为奇函数.
∴f()+f(-)=0.
(2)设-1< x1< x2 <1,
∵f(x2)-f(x1)= - x2+
log2
-[- x1+ log2
]
=( x1- x2)+ log2
,
∵x1- x2< 0, 1+x1-x2- x1x2-(1+x2-x1- x1x2)=2(x1- x2)<0,
∴1+x1-x2- x1x2< 1+x2-x1- x1x2.
∴0<<1. ∴log2< 0.
∴f(x2)-f(x1) < 0.
∴f(x)在(-1, 1)上单调递减.
当 a∈(-1, 1)当x∈ 时, 有最小值,且最小值为f(a)= -a+log2
.
21.解:设对甲种商品投资x万元，获总利润为y万元，
则对乙种商品的投资为(3-x)万元，y=
x+
(0≤x≤3).
令t= (0≤t≤
)，则x=3-t2,
∴y= (3-t2)+ t= (3+3t-t2)=- (t-
)2+
,t∈［0,］.
∴当t=时，ymax==1.05(万元)；
由t=可求得x=0.75(万元)，
3-x=2.25(万元),
∴为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元，
获得最高利润1.05万元.
22. 解析:（1）令
易得
．
而
且
，得
．
（2）设
，由条件（1）可得
，因
，
由（2）知
，所以
，即
在上是递减的函数．
由条件（1）及（I）的结果得：
其中
，
由函数在上的递减性，可得：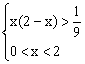
，
由此解得x的范围是
．
（3）同上理，不等式可化为
且，
得
，此不等式有解，等价于
，
在的范围内，易知
，
故
即为所求范围．