高一数学第一学期第一学段模块考试
高一年级数学必修1试卷
命题人:贾双喜 审题人:潘伟军
一、选择题:(本大题共18小题,每小题3分,共54分)
1、已知集合A={1,2,3,4},B={ 2,4,6},则AÇB=…………………( B )
| A. {1,3} | B. {2,4} | C. {1,6} | D. {2,3} |
2、设Q、P、R分别表示有理数集、无理数集、实数集,则QÈP=………( D )
| A. Q | B. P | C. Ø | D. R |
3、已知f(x-2)=![]() ,则函数f(x)的定义域为…………………………( B )
,则函数f(x)的定义域为…………………………( B )
| A. (0,+¥) | B. (-2,+¥) | C. (2,+¥) | D. (-¥,2) |
4、在下列函数:①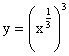 ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,与y=x表示同一函数的个数是……………………………………………………( A )
中,与y=x表示同一函数的个数是……………………………………………………( A )
| A. 1 | B. 2 | C. 3 | D. 4 |
5、化简:![]() …………………………………………………………( C )
…………………………………………………………( C )
| A. | B. | C. | D. |
6、右图中阴影部分所对应的集合是…………………………………………( C )
| A. (CUA)ÇB |
B. CU(AÈB) |
| C. (CUB)ÇA | D. CU(AÇB) |
7、把函数![]() 的图象向左平移1个单位,再向上平移2个单位后,所得函数的解析式应为………………………………………………………………( C )
的图象向左平移1个单位,再向上平移2个单位后,所得函数的解析式应为………………………………………………………………( C )
| A. | B. | C. | D. |
8、设函数f(x)=ax4+bx-3,则在下面给出的a、b的值中,使得f(x)为奇函数,且在(0,+¥)上单调递增的a、b的值分别是…………………………( B )
| A. a=0,b=1 | B. a=0,b=-1 | C. a=1,b=0 | D. a=-1,b=0 |
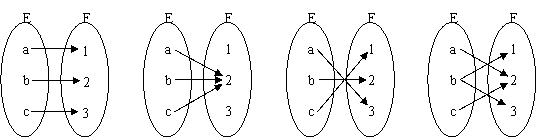
9、在下列集合E到集合F的对应中,不能构成E到F的映射是…………( D )
|
| B. | C. | D. |
10、函数![]() 与
与![]() 的图象关于………………………………( D )
的图象关于………………………………( D )
| A. x轴对称 | B. y轴对称 | C. 原点对称 | D. y=x对称 |
11、在下列函数中,是偶函数且在(-¥,0)上单调减少的函数是………( A )
| A. | B. | C. | D. |
12、若实数x、y满足x+log2y=0,则y关于x的函数的图象是…………( A )
|
| B. | C. | D. |
13、已知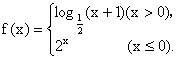 则f(f(0))=…………………………( A )
则f(f(0))=…………………………( A )
| A. -1 | B. 0 | C. 1 | D. 2 |
14、已知![]() ,则下列关系正确的是( D )
,则下列关系正确的是( D )
| A. AÇB=B | B. AÈB=B | C. AÇB=Æ | D. AÈB=R |
15、使得函数![]() 有零点的一个区间是……………………( C )
有零点的一个区间是……………………( C )
| A. (0,1) | B. (1,2) | C. (2,3) | D. (3,4) |
16、函数y=x+1-x的图象是………………………………………………( B )
|
| B. | C. | D. |
17、在0.20.3、0.30.2、log0.20.3和log0.30.2四个数中,最大的一个是…( D )
| A. 0.20.3 | B. 0.30.2 | C. log0.20.3 | D. log0.30.2 |
18、设![]() ,则…………………………………( B )
,则…………………………………( B )
| A. f(x)与g(x)都是奇函数 | B. f(x)是奇函数,g(x)是偶函数 |
| C. f(x)与g(x)都是偶函数 | D. f(x)是偶函数,g(x)是奇函数 |
二、填空题:(本大题共6小题,每小题3分,共18分)
19、计算:![]() 6 ;
6 ;
20、计算:![]() __
6 _____;
__
6 _____;
21、函数f(x)=2+log5(x+3)在区间[-2,2]上的值域是[2,3];
22、函数![]() 的定义域是 [-2,0)È(0,+¥)
;
的定义域是 [-2,0)È(0,+¥)
;
23、已知![]() 若f(x0)<1,则x0的取值范围是
(-1, 1) ;
若f(x0)<1,则x0的取值范围是
(-1, 1) ;
24、已知函数![]() ,在下列关于函数f(x)的判断:
,在下列关于函数f(x)的判断:
①是奇函数;②定义域为R;③值域为R;④是增函数;
⑤对任意的正实数x、y,等式f(xy)=f(x)+f(y)恒成立.
中,正确的有 ③、⑤ (只填序号).
三、解答题:(本大题共4小题,共28分)
25、(6分)已知集合A={xx2-2x-3<0},B=N(其中N为自然数集),
(1)用列举法表示集合AÇB;
(2)写出集合AÇB的所有子集.
解:(1)由x2-2x-3<0解得,-1<x<3,(1分)
又B=N ,\AÇB={0,1,2};(3分)
(2)AÇB的子集有:
Æ,{0},{1},{2},{0,1},{0,2},{1,2},{0,1,2}(6分)
(说明:漏掉1个扣1分)
26、(8分)已知函数![]() .
.
(1)写出函数f(x)的定义域,并证明函数f(x)是偶函数;
(2)用函数单调性的定义证明:函数f(x)在区间(0,+¥)上是减函数.
解:(1)因为x¹0,所以,函数f(x)的定义域为{xx¹0},(1分)
因为![]() ,\函数f(x)是偶函数;(4分)
,\函数f(x)是偶函数;(4分)
(2)设x2>x1>0,则x1+x2>0,x1-x2<0,(5分)
![]() (7分)
(7分)
\f(x2)<f(x1)
\函数f(x)在区间(0,+¥)上是减函数. (8分)
27、(6分)在年均增长率相同的情况下,经过4年深圳的GDP可以翻一翻(即原来的2倍).那么,在年均增长率不变的情况下,大约需要经过多少年,深圳的GDP是目前的5倍?(精确到年.数据lg2»0.30可供参考)
解:设年均增长率为r,大约需要经过x年,深圳的GDP是目前的5倍,(1分)则
(1+r)4=2,(1+r)x=5(3分)
从而有
![]() ,\
,\![]() (4分)
(4分)
两边取常用对数,得
![]() ,
,![]() (年)
(年)
答:大约需要经过9年,深圳的GDP是目前的5倍. (6分)
28、(8分)设函数![]() .
.
(1)当a=1时,求函数f(x)的单调区间;
(2)若函数f(x)的定义域为R,求实数a的取值范围;
(3)若函数f(x)的值域为R,求实数a的取值范围.
解:(1)当a=1时,![]() ,x必须满足:
,x必须满足:
x2-x-2>0,解得,x<-1或x>2,
\函数f(x)的定义域为{x x<-1或x>2}(2分)
因为![]() 在区间(-¥,-1)上是减函数,又
在区间(-¥,-1)上是减函数,又![]() 是减函数,所以,函数f(x)的单调增区间是(-¥,-1);
是减函数,所以,函数f(x)的单调增区间是(-¥,-1);
同理,可求得函数f(x)的单调减区间是(2,+¥). (4分)
(2)因为函数f(x)的定义域为R,所以,
对任意的实数x,不等式x2-ax-2a>0恒成立.所以
D=a2-4(-2a)<0 ,即a2+8a<0,解之得,-8<a<0,
故,所求实数a的取值范围是-8<a<0.(6分)
(3)因为函数f(x)的值域为R,所以,x2-ax-2a的值域包含R+,即
方程x2-ax-2a=0有实数根.所以
D=a2-4(-2a)³0 ,即a2+8a³0,解之得,a£-8或a³0,
故,所求实数a的取值范围是a£-8或a³0.(8分)
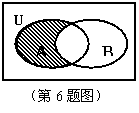
 A.
A.  A.
A. 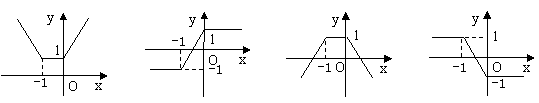 A.
A.