高一数学第一次联考试题
第I卷
一、选择题：本大题共10小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的，并将答案填涂在答题卡上.
1.下列表示错误的是 ( )
A.
B.
C.
D.
2.设集合A.=
,则
( )
A.
B.
C.
D.
3.函数
的定义域为
( )
A. 
B.
C.
D.
4.下列函数中,表示同一函数的是 ( )
A. 
与
B.
与
C. 
与
D. 
与
.
5. 函数
（
是以
为底的对数）的零点落在区间( )
A．（2，2.25） B．（2.25，2.5） C．（2.5，2.75） D．（2.75，3）
6. 函数
，
的递增区间是
(
)
A. 
B.
C.
D. 
7. 函数
的图象和函数
的图象的交点个数是 （ ）
A．4 B．3 C．2 D．1
8. 已知
，求
在区间
上的最大值与最小值 ( )
A．2与1 B． 3与1 C．9与3 D．8与3
9.给出下列三个等式：
，
， 
，下列函数中不满足其中任何一个等式的是
（ ）
A．
B．
C．
D．
10.已知
,且
,
( )
A.奇函数 B.偶函数
C.非奇非偶函数 D.奇偶性与
有关
第II卷
二、填空题：本大题共4小题，每小题5分．
11. 已知
，其中
，则
的值域为
；
12. 给出函数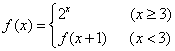
,则
；
13.已知定义在
上的奇函数
,当
时，
，则
；
；
14.已知函数
在
上是增函数,则实数
的取值范围是____
______ ；
三、解答题(共6个小题,共80分；解答应写出文字说明,证明过程或演算步骤)
15. 计算下列各式的值(每小题6分,共12分)
(1) 
(2) 
16 .(12分）比较下列各数的大小，并写出理由.
（1）
与
；
（2）
与
；
（3）
与
；
17．（14分）如图，直角梯形OABC位于直线
右侧的图形面积为
.
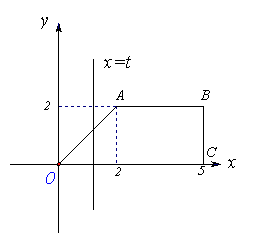（1）试求函数的解析式； （2）画出函数
的图象.
 |
18.（14分）已知函数
是定义域
上的奇函数，
（1）求
的值，并写出的表达式；
（2）试判断的单调性，并证明 .
19．(14分)已知全集
，集合
，集合
,已知
，
（1）求
，
；
（2）若
,求实数的取值范围.
20．（14分）已知定义域为
的函数同时满足以下三个条件：
[1] 对任意的
，总有
；
[2] 
；
[3] 若
，
，且
，则有
成立，
并且称为“友谊函数”，请解答下列各题：
(1)若已知为“友谊函数”，求
的值；
(2)函数
在区间上是否为“友谊函数”？并给出理由.
(3)已知为“友谊函数”，假定存在
，使得
且
，
求证：
.
2007-----2008学年度第一次联考试题 高一数学答案:
一.选择题: ADCDC ADABA
二.填空题:11. 
12.
8
13. 0；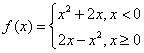
14. 
三.解答题:
15. 计算下列各式的值(每小题6分,共12分)
(1) (2)
解:(1)原式=(0.4
-2分 (2)原式= 
--2分
=0.4
----------4分 =
--4分
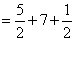---------------5分 =
----------5分
=10. --------------------6 分 =1.----------------------- 6分
16．(12分）比较下列各数的大小，并写出理由.
（1）与；
（2）与；
（3）与
；
解：（1）
（2分），理由
在上单调减，又
故（4分）
（2）
（2分）， 理由
在
上单调减，
又
故（4分）
（3）
（2分） 理由：
(2分).
17、解：（1）设直线
与梯形的交点为D，E.--------------------------1分
当
时
-----------------------4分
当
时，
-------------------7分
所以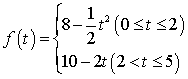
--------------------------------------------------------8分
（2）标明轴的坐标------------9分
画出的图象--------------------------------------------------------------------12分
画出的图象--------------------------------------------------------------------14分
图象（略）
18、(1)由因为定义域为，所以
，-------4分；故
;----6分；
（2）证明略；---------------------------------------------------------14分.
19、解：（1）集合
，
，
所以
------------------------------------4分
又
，
---------------4分
（2）又
欲使，须分类讨论：
[1] 当时，
，结合数轴可得：
；---10分
[2] 当
时，
为空集，不符合题意，舍去；---------11分
[3] 当
时，
，结合数轴可知无解；----13分
综上所述，.---------------------------------------14分
20. （1）取
得
，-------2分
又由
，得
--------------- 3分
（2）显然在上满足[1] 
；[2] 
.-------5分
若，，且，则有
故满足条件[1]、[2]、[3]，所以为友谊函数.------8分
(3)由 [3]知任给
其中
，且有
，不妨设
则必有：
---------------------------------------9分
所以：
所以：
.-------------------------------------10分
依题意必有,
下面用反证法证明：假设
，则有
或
(1) 若，则
，这与矛盾；----12分
(2)若，则
，这与矛盾；
故由上述（1）、（2）证明知假设不成立，则必有，证毕.-------14分