高一数学第二学期半期考
高一数学(必修2)试题
（完卷时间:120分钟；满分:150分）
一、选择题（每小题12分，共60分，把答案填在Ⅱ卷中）
1. 直线
的倾斜角是（ ）
A.135° B. 45° C. 30° D. 60°
2.
若直线
∥平面
，直线
，则
与
的位置关系是（ ）
A、∥
B、与异面 C、与相交 D、与没有公共点
3. 在同一直角坐标系中，表示直线
与
正确的是（ ）
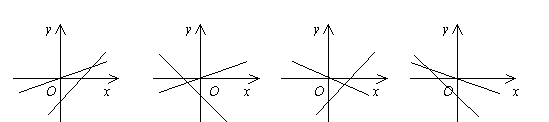A． B． C． D．
4. 下列命题中正确的是（ ）
A．由五个平面围成的多面体只能是四棱锥
B．棱锥的高线可能在几何体之外
C．仅有一组对面平行的六面体是棱台
D．有一个面是多边形，其余各面是三角形的几何体是棱锥
5. 已知直线a、b与平面α、β、γ，下列条件中能推出α∥β的是（ ）
A．a⊥α且a⊥β B．α⊥γ且β⊥γ
C．a
α，bβ，a∥b D．aα，bα，a∥β，b∥β
6. 不论
取任何实数，直线
恒过一定点，则该定点的坐标是（ ）
A． （-1，2） B.(-1,-2) C .(1 ,2) D. (1,-2)
7. 已知直线
与直线
平行，则它们之间的距离是（ ）
A．
B．
C．8
D．2
8. 设是空间的三条直线，给出以下五个命题：
①若a⊥b，b⊥c，则a⊥c； ②若a、b是异面直线，b、c是异面直线，则a、c也是异面直线；
③若a和b相交，b和c相交，则a和c也相交；④若a和b共面，b和c共面，则a和c也共面；
⑤若a∥b， b∥c，则a∥c； 其中正确的命题的个数是（ ）.
A.0 B.1 C.2 D.3
9. 若三棱锥P-ABC的三条侧棱与底面所成的角都相等，则点P在底面ABC上的射影一定是DABC的（ ）
A. 外心 B. 垂心 C. 内心 D. 重心
10. 中心角为135°的扇形，其面积为B，其围成的圆锥的全面积为A，则A：B为（ ）
A．11：8 B．3：8 C．8：3 D．13：8
11. 直线x－2y+1=0关于直线x=1对称的直线的方程是（ ）
A. x+2y－1=0 B. x+2y－3=0 C. 2x+y－1=0 D. 2x+y－3=0
12. 已知点P是圆(x－3)2+y2=1上的动点，则点P到直线y=x+1的距离的最小值是（ ）
A. 3 B. 2
C. 2－1 D. 2+1
二、填空题：（本大题共4小题，每小题4分，共16分。把答案填在Ⅱ卷中的横线上）
13. 已知直线x－y+2=0与直线(2－1)x+y+1=0
(≠0) 互相垂直,则=
14. 
过点（1，2）且在两坐标轴上的截距相等的直线的方程
_；
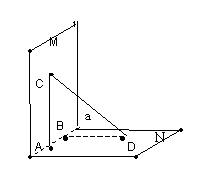
15. 如图所示，平面M、N互相垂直，棱a上有两点A、B，ACM，BDN，且AC⊥a，BD⊥a, AB＝12cm，AC＝3 cm，BD＝4cm，则CD＝____ ___．
( (第21题图)
16. 
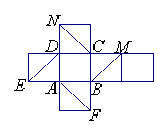如图是一个正方体纸盒的展开图，
在原正方体纸盒中有下列结论：
①BM与ED平行；②CN与BE是异面直线；
③CN与BM成
角；④DM与BN垂直．
其中，正确命题的序号是__ ．
(第16题图)
三、解答题（本大题共6小题，共74分，解答写出文字说明、证明过程或演算步骤）
17. 已知点A（2，－3）和B（－2，－5）， （1）求直线AB的斜率；
（2）如果圆C经过A、B两点，且圆心在直线l：
上，求圆C的标准方程．
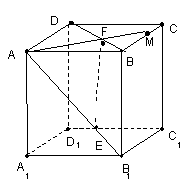
18. 如图，正方体ABCD—A1B1C1D1中，E在AB1上，
F在BD上，且B1E＝BF.
(1)求直线AB1 和平面A1B1C1D1 所成的角大小。
(2)求证：EF∥平面BB1C1C.
(第18题图)
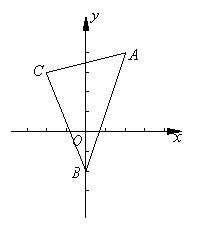
19. 如图，已知三角形的顶点为
，
，
，求：
（Ⅰ）AB边上的中线CM所在直线的方程；
（Ⅱ）求△ABC的面积．
(第19题图)
20. 
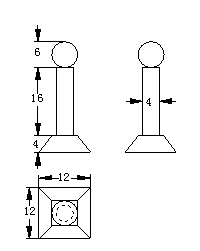如图，是一个奖杯的三视图（单位：cm），
底座是正四棱台．
（Ⅰ）求这个奖杯的体积（
取
）；
（Ⅱ）求这个奖杯底座的侧面积．
(第20题图)
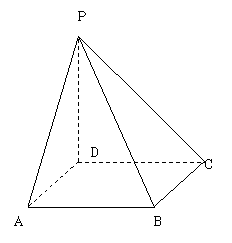
21. 如图,已知三棱锥A－BCD的三条侧棱AB、AC、AD两两垂直.
(Ⅰ)试问：三个侧面ABC、ABD、ACD是否两两垂直？并说明理由;
(Ⅱ)若AB=AC=AD=, 求三棱锥的全面积; (侧面积+底面积)
(Ⅲ)在平面几何里, 有勾股定律:
"若三角形ABC的两边AB、AC互相垂直,则两条直角边长的平方和等于斜边长的平方, 即 AB2+AC2=BC2
". 类比平面几何的勾股定律,研究这个三棱锥的侧面积与底面积的关系, 写出正确的结论.
22. 四棱锥P－ABCD中，底面ABCD是正方形，
边长为，PD=，PD⊥平面ABCD
（1）求证: AC⊥PB ；
（2）求二面角A－PB－D的大小；
（3）求四棱锥外接球的半径．
（4）在这个四棱锥中放入一个球，求球的最大半径；
(第22题图)