高一数学第二学期期中考试
高一数学试题
一、填空题:
1.第一届现代奥运会于1896年在希腊雅典举行,此后每4年举行一次,奥运会如因故不能举行,届数照算。那么2008年北京奥运会是第 __ ___届。
2.在![]() ABC中,
ABC中,![]() 、b、c分别为
、b、c分别为![]() A、
A、![]() B、
B、![]() C的对边,若A:B:C=1:1:4,则
C的对边,若A:B:C=1:1:4,则![]() = __
= __
3.等比数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() ___ ____
___ ____
4.在![]() ABC中,
ABC中,![]() 、b、c分别为
、b、c分别为![]() A、
A、![]() B、
B、![]() C的对边,若
C的对边,若![]() ,则A=___ ___
,则A=___ ___
5.等差数列![]() 的公差d≠0,又
的公差d≠0,又![]() 成等比数列,则
成等比数列,则![]() =___
____
=___
____
6.在△ABC中,![]() 、b、c分别为
、b、c分别为![]() A、
A、![]() B、
B、![]() C的对边,
C的对边,![]() ,则△ABC的形状为___ ____
,则△ABC的形状为___ ____
7.函数![]() 的最大值是___ ___
的最大值是___ ___
![]()
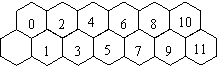
8.观察蜜蜂爬过六角形蜂房所取的不同路线(如图) ,假定该蜜蜂总是向相邻的蜂房移动,并且总是向右移动,那么,蜜蜂到蜂房0有1条路,到蜂房1有2条路,到蜂房2有3条路,到蜂房3有5条路,依此规律,蜜蜂到蜂房10有___ ____条路。
9.不等式![]() 的解集是___ ____
的解集是___ ____
10.在![]() ABC中,
ABC中,![]() =4,A=300,b=4
=4,A=300,b=4![]() ,则
,则![]() ABC的面积为___ ____
ABC的面积为___ ____
11.不等式![]() <0对任意实数x恒成立,则m的取值范围为 ___ ____
<0对任意实数x恒成立,则m的取值范围为 ___ ____
12.小明是淮阴中学2007级高一(1)班学生,为他将来读大学的费用做好准备,他的父母计划从2008年7月1日起至2010年7月1日每月定期到银行存款m元(按复利计算),2010年8月1日全部取出,月利率按2%0计算,预计大学费用为4万元,那么m=__ ___
(计算结果精确到元。可以参考以下数据:![]()
![]()
![]() )
)
13.下列结论中正确的是___ ____
①等差数列![]() 的前n和为Sn,则数列:Sn,S2n-Sn,S3n-S2n,……为等差数列;
的前n和为Sn,则数列:Sn,S2n-Sn,S3n-S2n,……为等差数列;
②等比数列![]() 的前n和为Sn,则数列:Sn,S2n-Sn,S3n-S2n,……为等比数列;
的前n和为Sn,则数列:Sn,S2n-Sn,S3n-S2n,……为等比数列;
③等比数列![]() 的前n积为Tn,则数列:Tn,
的前n积为Tn,则数列:Tn,![]() ,
,![]() ,……为等比数列;
,……为等比数列;
④等差数列![]() 的前n和为Sn,若数列:Sn,S2n-Sn,S3n-S2n,……为常数数列,则数列
的前n和为Sn,若数列:Sn,S2n-Sn,S3n-S2n,……为常数数列,则数列![]() 的公差为0;
的公差为0;
⑤等比数列![]() 的前n和为Sn,若数列:S2n,S4n-S2n,S6n-S4n,……为常数数列,则数列
的前n和为Sn,若数列:S2n,S4n-S2n,S6n-S4n,……为常数数列,则数列![]() 的公比为1。
的公比为1。
14.设A为锐角三角形的内角,![]() 是大于0的正常数,函数
是大于0的正常数,函数![]() 的最小值是9,则
的最小值是9,则![]() 的值等于___ ____
的值等于___ ____
二、解答题:(本大题共90分)
15.(14分)已知集合![]() ,集合
,集合![]()
(1)求集合A、B;
(2)若B![]() A,求m的取值范围。
A,求m的取值范围。
16.(14分)设![]() 为等差数列,
为等差数列,![]() 为等比数列,且
为等比数列,且![]() ,若
,若![]() , 且
, 且![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的公差
的公差![]() 和
和![]() 的公比
的公比![]() ; (2)求数列
; (2)求数列![]() 的前10项和。
的前10项和。
17. (15分)投资生产A产品时,每生产100t需要资金200万元,需场地200m2,可获利润300万元;投资生产B产品时,每生产100m需要资金300万元,需场地100m2,可获利润200万元。现某单位可使用资金1400万元,场地900m2,问:应作怎样的组合投资,可使获利最大?
18.(15分)在△ABC中,![]() 分别为角A、B、C的对边,
分别为角A、B、C的对边,![]() ,
,![]() =3, △ABC的面积为6,D为△ABC内任一点,点D到三边距离之和为d。
=3, △ABC的面积为6,D为△ABC内任一点,点D到三边距离之和为d。
(1)求角A的正弦值; (2)求边b、c; (3)求d的取值范围。
19.(16分)已知数列![]() 的前
的前![]() 项和
项和![]() 和通项
和通项![]() 满足
满足![]() (
(![]() 是常数且
是常数且![]() )。
)。
(1)求数列![]() 的通项公式;
(2)当
的通项公式;
(2)当![]() 时,试证明
时,试证明![]() ;
;
(3)设函数![]() ,
,![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 对任意
对任意![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
20.(16分)己知集合M={(x,y)x>0,y>0,x+y=k},其中k为正常数。
(1)设t=xy,求t的取值范围;
(2)求证:当k≥1时,不等式![]() 对任意(x,y)
对任意(x,y)![]() 恒成立;
恒成立;
(3)求使不等式![]() 对任意(x,y)
对任意(x,y)![]() 恒成立的k的范围。
恒成立的k的范围。
高一数学试题参考答案及评分标准
1.29
2.![]() 3.-1
4.450 5.
3.-1
4.450 5.![]()
6.等腰
7.![]() 8.144
9.
8.144
9.![]() 10.
10.![]()
11.![]() 12.1569 13.①③④ 14.4
12.1569 13.①③④ 14.4
15.解:(1) ![]()
![]() ----(3′)
----(3′) ![]() 即A={x
即A={x![]() } --------(5′)
} --------(5′)
![]()
![]() -------------------------------------(8′)
-------------------------------------(8′)
![]() 即A={x
即A={x![]() }
------------------------------------------------------(10′)
}
------------------------------------------------------(10′)
(2) B![]() A
A![]() -----------------(12′)
-----------------(12′) ![]() --------------------------(14′)
--------------------------(14′)
16.解:(1)![]() ,
,![]() ---------------------------------------------(1′)
---------------------------------------------(1′)
由![]() ,
,![]() 得
得![]() --------(4′) 解得:
--------(4′) 解得:![]() 或
或![]() (舍)--------------(6′)
(舍)--------------(6′)
所以,![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() 。
-------------------------------------------------(8′)
。
-------------------------------------------------(8′)
(2)![]() =
=![]() --------------------- (10′)
--------------------- (10′)
=![]() =978
----------------------------------------------------------(14′)
=978
----------------------------------------------------------(14′)
17.解:设生产A产品x百吨,生产B产品y百米,利润为S 百万元----------------(1′)
则约束条件为: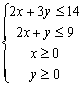 , --------(5′) 目标函数为S=3x+2y,------(7′)
, --------(5′) 目标函数为S=3x+2y,------(7′)
作出可行域,(图略) ---------------------------------------------------------------------------------(11′)
使目标函数为S=3x+2y取最大值的(x,y)是直线2x+3y=14与2x+y=9的交点(3.25,2.5),
此时S=3×3.25+2×2.5=14.75-----------------(13′) 答:(略) -----------------------(15′)
18.解:(1) ![]()
![]()
![]()
![]()
![]()
![]()
![]() --------------(4′)
--------------(4′)
(2)![]()
![]() ,
,![]() 20
----------------------------------------------(6′)
20
----------------------------------------------(6′)
由![]() 及
及![]() 20与
20与![]() =3解得b=4,c=5或b=5,c= 4 -----------------------(10′)
=3解得b=4,c=5或b=5,c= 4 -----------------------(10′)
(3)设D到三边的距离分别为x、y、z,则![]() -----------------(11′)
-----------------(11′)
![]() ------------(12′) 又x、y满足
------------(12′) 又x、y满足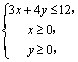 -----------(13′)
-----------(13′)
画出不等式表示的平面区域得:![]() ---------------------------------------------------(15′)
---------------------------------------------------(15′)
19.解:(1)当![]() 时,
时,![]() ------------------(2′)
------------------(2′)
![]()
![]() -----------------(2′) 又由
-----------------(2′) 又由![]()
![]() 得
得![]() -------------(3′)
-------------(3′)
∴数列![]() 是首项
是首项![]() 、公比为
、公比为![]() 的等比数列, ∴
的等比数列, ∴ ![]() -------------(5′)
-------------(5′)
(2) 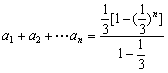 ---------------(7′) =
---------------(7′) =![]() --------------(9′)
--------------(9′)
(3)![]()
![]() ------(9′)
------(9′)
![]()
![]() -------------------------(11′)
-------------------------(11′)
![]() 即
即![]()
![]() ,
,![]() ---------------------------------------------------(14′)
---------------------------------------------------(14′)
∵![]() 是正整数,∴
是正整数,∴![]() 的值为1,2,3。 -----------------------------------------------------(16′)
的值为1,2,3。 -----------------------------------------------------(16′)
20.解:(1)t=xy![]() ,
---------------------------------------------------- (2′)
,
---------------------------------------------------- (2′)
当x=y=k时取等号,所以xy取值范围为![]() ------------------------------------- (4′)
------------------------------------- (4′)
(2)![]() -------------- (6′)
-------------- (6′)
![]() ,故
,故![]()
![]() 在
在![]() 为增函数, ------------------------(8′)
为增函数, ------------------------(8′)
![]()
![]() --------------------------------------------- (10′)
--------------------------------------------- (10′)
(3)由(2)知![]() ,
,![]() 即求
即求![]() 对
对![]()
![]() 恒成立的k的范围 --------(11′)
恒成立的k的范围 --------(11′)
又![]()
![]()
![]() 上递减,在
上递减,在![]() 上递增, --------(13′)
上递增, --------(13′)
要使函数![]() 在
在![]() 上恒有
上恒有![]() ,则必须
,则必须![]() , ------------------(14′)
, ------------------(14′)
解得![]() -----------------------------------------------------------------------------(16′)
-----------------------------------------------------------------------------(16′)