高一数学同步导学训练 必修五
期中复习试卷（二）
班级______________姓名_____________学号_________
1、不等式
的解集是__________
2、在等比数列
，
，则公比
=________
3、已知数列
中，
，
，则
的值为_________
4、在各项均为正数的等比数列
中，若
，则
……
____
5、在
中，若
，则为___________三角形
6、已知等差数列满足
=28，则该数列前10项之和为
7、中，
、
、
分别为∠A、∠B、∠C的对边，若，，成等差数列，
，的面积为
，那么
_________
8、数列满足
，
，则
=
9、已知
，则
的最小值为____________
10、若的三个内角
成等差数列，
，
，则边
上的中线
的长为
11、两等差数列
和
,前
项和分别为
,且
则
12、的三角所对的边
成等比数列，则
的取值范围是________
13、数列的前项和
，则
14、建造一个容积为18m3, 深为2m的长方形无盖水池，如果池底和池壁每1m2 的造价分别为200元和150元，那么池的最低造价为 元
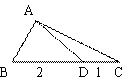
15、中，
在边上，且
，
，
，
，求
的长及的面积。
16、已知实数
成等差数列，
，
，
成等比数列，且
，求
17、在中，已知
，试判断三角形的形状
18、已知数列
为等差数列，且
，
（1）求数列的通项公式；（2）求数列的前项和
19、经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量
（千辆/小时）与汽车的平均速度
（千米/小时）之间的函数关系为：
．
（1）在该时段内，当汽车的平均速度为多少时，车流量有何最大值？（保留分数形式）
（2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？
参考答案：
1、
或
； 2、
； 3、52； 4、7； 5、等腰三角形； 6、140；
7、
；
8、
； 9、
；
10、
； 11、
； 12、
；
13、48； 14、5400；
15、解：在△ABC中，∠BAD＝150o－60o＝90o，∴AD＝2sin60o＝
．
在△ACD中，AC2＝()2＋12－2××1×cos150o＝7，∴AC＝
．
∴AB＝2cos60o＝1．S△ABC＝
×1×3×sin60o＝
．
16、解：由题意，得
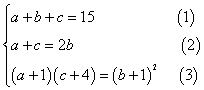由（1）（2）两式，解得
，将
代入（3），整理得
17、证：
化简整理得
由正弦定理得
或
18、解:设等差数列
的公差为d. 
解得d=1.
所以
19、解：（Ⅰ）依题意，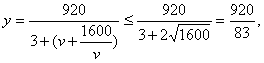
当且仅当
，即
时，
（千辆/小时）
（Ⅱ）由条件得
整理得v2－89v+1600<0,
即（v－25）（v－64）<0,解得25<v<64.
答：当v=40千米/小时，车流量最大，最大车流量约为11.1千辆/小时.如果要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应大于25千米/小时且小于64千米/小时．