高一数学同步导学训练 必修五
期中复习试卷（三）
班级_______________姓名________________学号_____
1、在
中,
，则
_______
2、在中，
，则A等于_____
3、已知等差数列
中，
，
，
的值是_______
4、在等比数列{an}中，
=1，
=3，则
的值是________
5、对于任意实数
，以下5个命题中①若
，则
；②若
，则
；③若，则；④若，则
；⑤若
，则
．正确的个数是_______个
6、已知不等式
的解集为
，则不等式
的解集____
7、已知等比数列
的公比
，则
______
8、中，
、
、
，
在内部及边界运动，则
的最大值为___________；最小值为__________
9、函数
的最大值为
10、在数列
中，
，且对于任意正整数
，都有
，则
_____
11、若
，
，则的最小值为_______
12、已知
，则不等式
的解集是_________
13、已知
，则
的最小值为________
14、已知数列的通项公式
, 则该数列的前项和
_____________
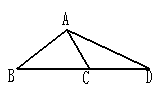15、如图，已知
，
，
，
，求：（1）AC，AD的长；（2）求
16、已知函数
的图象经过点
和
，记
（1）求数列的通项公式；（2）的前项和；
17、某种汽车购买时费用为
万元，每年应交付保险费、养路费及汽油费共
万元，汽车的维修费为：第一年
万元，第二年
万元，第三年
万元，……，依等差数列逐年递增．
（1）设使用年该车的总费用（包括购车费用）为
，试写出的表达式；
（2）求这种汽车使用多少年报废最合算（即该车使用多少年平均费用最少）。
18、设是正数组成的数列，其前项和为
，并且对于所有的，都有
（1）写出数列的前3项； （2）求数列的通项公式(写出推证过程)；
（3）设
，
是数列
的前项和，求使得
对所有都成立的最小正整数
的值
1、
； 2、
； 3、15； 4、16； 5、1个；
6、
或
；
7、
； 8、6、1； 9、
； 10、
； 11、7；
12、
；
13、
； 14、
；
15、解：（1）在中，由正弦定理得：
在
中，由余弦定理得：
，得AD=7
（2）
16、解：（1）由已知可知：
，
所以
，解得
。
。
（2）
，对
恒成立，
所以是以1为首项，2为公差的等差数列。所以
17、依题f(n)=14.4+(0.2+0.4+0.6+…+0.2n)+0.9n
（2）设该车的年平均费用为S万元，则有
仅当
，即n=12时，等号成立.
故：汽车使用12年报废为宜.
18、解:(1) n=1时 
∴
n=2时 
∴
n=3时 
∴
(2)∵
∴
两式相减得: 
即
也即
∵
∴
即是首项为2,公差为4的等差数列∴
(3)
∴
∵
对所有
都成立 ∴
即