高一数学同步导学训练 必修五
期中复习试卷（四）
班级________________姓名______________学号______
1、已知△ABC的周长为9，且
，则cosC＝
.
2、在
中, 若
,则的外接圆的半径为 _________
3、在△ABC中，B＝135°，C＝15°，a＝5，则此三角形的最大边长为
4、若各项均为正数的等比数列
，
，
，则
_____；前n项和
＝
5、已知等差数列
的前
项的和为
，若
，则
________
6、已知等差数列
的公差为2 , 若
成等比数列, 则
的值为________
7、已知数列的前项的和
，则通项公式___________
8、在中,若
则的形状一定是_________三角形
9、已知数列满足，
（
），则__________
10、若
成等比数列，
是
的等差中项，是
的等差中项，则
_____
11、变量
满足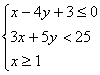
，则目标函数
的最小值是_______
12、已知两个正数满足
，则使不等式
恒成立的实数的范围是____
13、为钝角三角形，
,
,
,角
为钝角，则
的取值范围为________
14、一个首项为正数的等差数列的前项和
满足：
，则当最大时，
____
15、已知是中角
的对边,
是的面积.若
,求边
的长度.
16、设等差数列{
}的前项和为，已知
＝
，
．
(1) 求；（2）求数列{}的前n项和；（3）当n为何值时，最大，并求的最大值．
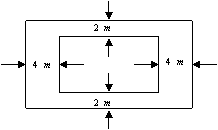
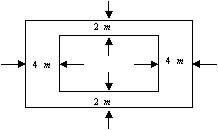
17、学校要建一个面积为
的长方形游泳池，并且在四周要修建出宽为
和
的小路（如图所示）。问游泳池的长和宽分别为多少米时，占地面积最小？并求出占地面积的最小值。
18、已知集合
，
（1）当
时，求
； （2）求使
的实数
的取值范围
1、
； 2、
； 3、
； 4、
、
； 5、72； 6、
；
7、
； 8、等腰三角形； 9、
； 10、2； 11、3；
12、
； 13、
； 14、7或8；
15、解: 
或
或
, 
或
.
16、解：（1）依题意有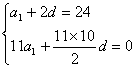
，解之得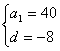
，∴
.
（2）由（Ⅰ）知，
＝40，， ∴ ＝
＝
.
（3）由（Ⅱ）有，＝＝－4
＋121，
故当
或
时，最大，且的最大值为120.
17、解：设游泳池的长为
，则游泳池的宽为
, 又设占地面积为
，依题意，
得
当且仅当
,即
时,取“=”.
答：游泳池的长为
,宽为
时，占地面积最小为648
18、解：（Ⅰ）当a＝2时，A＝（2，7），B＝（4，5），∴ A
B＝（4，5）.
（Ⅱ）∵ B＝（2a，a2＋1），当a＜
时，A＝（3a＋1，2），
要使B 
A，必须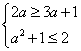
，此时a＝－1；当a＝时，A＝
，使B A的a不存在；
当a＞时，A＝（2，3a＋1），要使B A，必须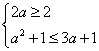
，此时1≤a≤3.
综上可知，使B A的实数a的取值范围为[1，3]∪{－1}.