高一数学同步导学训练 必修五
期中复习试卷（五）
班级_________________姓名_______________学号________
1、若4，
，16成等比数列，则
______
2、设等差数列
的前n项之和为
，已知
，则
_____
3、已知
是数列
的前
项和，
，则
______
4、在
中，已知
，则
________
5、求值：
___________
6、不等式
的解集是__________
7、关于的不等式
的解集为
8、设
，
，
，则
的最小值是_________
9、在数列中，已知前项和
,则数列的通项公式
________
10、等差数列
的前
项和为5，前
项和为50，则它的前
的和为________
11、数列中
，
，若
，则
___
12、若对于一切正实数不等式
>
恒成立，则实数的取值范围是
13、等差数列中,
则使前项和
成立的最大自然数为________
14、双休日，小明和小岳经过父母同意后去登山，小明以每小时公里的速度上山，以每小时
公里的速度沿原路下山，小岳上山和下山的速度都是每小时
公里，若两人在同一起点同时出发走同一条路，则先回到起点的是____________
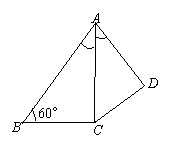
15、如图，在四边形
中，
平分
，
，
，
，
，求
的长
16、已知
，
（1）当
时，解不等式
； （2）若
，解关于x的不等式
17、数列满足
，
（
）
（1）求证
是等差数列； （2）若
，求的取值范围。
18、某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元。该公司第年需要付出设备的维修和工人工资等费用
的信息如下图。
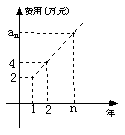（1）求； （2）引进这种设备后，第几年后该公司开始获利；
（3）这种设备使用多少年，该公司的年平均获利最大？
19、已知函数
，设
，
（1）求
，
的表达式，并猜想
的表达式（直接写出猜想结果）
（2）若关于的函数
在区间
上的最小值为6，求的值。
1、
； 2、20； 3、1016； 4、
； 5、
； 6、
；
7、
； 8、
； 9、
； 10、135； 11、4008；
12、
； 13、4006； 14、小岳；
15、解：在△ADC中，已知AC＝6，AD＝5，S△ADC＝
，
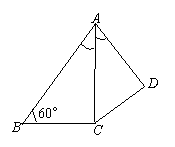则由S△ADC＝
·AC·AD·sin∠DAC，求得sin∠DAC＝，即∠DAC＝30°，
∴ ∠BAC＝30°.
而∠ABC＝60°，故△ABC为直角三角形.
∵ AC＝6，∴ AB＝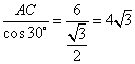
16、解：（1）当时，有不等式
，
∴
，∴不等式的解为：
（2）∵不等式
当
时，有
，∴不等式的解集为
；
当
时，有
，∴不等式的解集为
；
当
时，不等式的解为
。
17、解：（I）由可得：
所以数列
是等差数列，首项
，公差
∴
∴
（II）∵
∴
∴ 
解得
解得的取值范围：
18、解：（1）每年的费用是以2为首项，2为公差的等差数列，求得：
（2）设纯收入与年数n的关系为f(n),则：f(n)=21n-[2n+
]-25=20n-n2-25
由f(n)>0得n2-20n+25<0 解得
又因为n
,所以n=2,3,4,……18.即从第2年该公司开始获利
（2）年平均收入为
=20-
当且仅当
时，年平均收益最大.所以这种设备使用5年，该公司的年平均获利最大。
19、（1）
，
，
猜想
（2）
，
，
，又
在区间上的最小值为6
当
时，
，解得
，