高一数学第一学期授课讲义
讲义十二:指数与指数幂的运算
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:
1、了解指数函数模型背景及实用性、必要性,了解根式的概念及表示方法. 理解根式的概念.2、使学生正确理解分数指数幂的概念,掌握根式与分数指数幂的互化,掌握有理数指数幂的运算. 3、 n次方根的求解,会用分数指数幂表示根式, 掌握根式与分数指数幂的运算.
二、教学重点:
理解根式的概念,了解指数函数模型的应用背景;掌握n次方根的求解. 掌握根式与指数幂的运算;有理数指数幂的运算.
三、教学难点:
准确运用性质进行计算. 有理数指数幂的运算.无理数指数幂的意义.
四、教学过程:
(一)、复习准备: 回顾初中根式的概念:如果一个数的平方等于a,那么这个数叫做a的平方根;如果一个数的立方等于a,那么这个数叫做a的立方根. → 记法:![]()
(二). 讲授新课:
1. 教学指数函数模型应用背景:
① 探究下面实例,了解指数指数概念提出的背景,体会引入指数函数的必要性.
★实例1.某市人口平均年增长率为1.25℅,1990年人口数为a万,则x年后人口数为多少万?
★② 书P52 问题1. 国务院发展研究中心在2000年分析,我国未来20年GDP(国内生产总值)年平均增长率达7.3℅, 则x年后GDP为2000年的多少倍?
★ 书P52 问题2. 生物死亡后,体内碳14每过5730年衰减一半(半衰期),则死亡t年后体内碳14的含量P与死亡时碳14的关系为![]() . 探究该式意义?
. 探究该式意义?
③小结:实践中存在着许多指数函数的应用模型,如人口问题、银行存款、生物变化、自然科学.
2. 教学根式的概念及运算:
(1) 定义n次方根:一般地,若![]() ,那么
,那么![]() 叫做
叫做![]() 的
的![]() 次方根.(
次方根.( ![]() th root ),其中
th root ),其中![]() ,
,![]()
简记:![]() . 例如:
. 例如:![]() ,则
,则![]()
(2)、 讨论:当n为奇数时, n次方根情况如何?, 例如: ![]() ,
,![]() , 记:
, 记:![]()
当n为偶数时,正数的n次方根情况? 例如: ![]() ,
,![]() 的4次方根就是
的4次方根就是![]() , 记:
, 记:![]()
强调:负数没有偶次方根,0的任何次方根都是0, 即. ![]()
(3)、 练习:![]() ,则
,则![]() 的4次方根为 ;
的4次方根为 ; ![]() , 则
, 则![]() 的3次方根为 .
的3次方根为 .
(4)、定义根式:像![]() 的式子就叫做根式(radical), 这里n叫做根指数(radical
exponent), a叫做被开方数(radicand).
的式子就叫做根式(radical), 这里n叫做根指数(radical
exponent), a叫做被开方数(radicand).
(5)、计算![]() 、
、![]() 、
、![]() → 探究:
→ 探究: ![]() 、
、![]() 的意义及结果? (特殊到一般)
的意义及结果? (特殊到一般)
结论:![]() . 当
. 当![]() 是奇数时,
是奇数时,![]() ;当
;当![]() 是偶数时,
是偶数时,![]()
(6)、出示例1.求值化简: ![]() ;
; ![]() ;
; ![]() ;
; ![]() (
(![]() )
)
3. 教学分数指数幂概念及运算性质:
① 引例:a>0时,![]() →
→ ![]() ;
; ![]() →
→ ![]() .
.
② 定义分数指数幂:规定![]() ;
;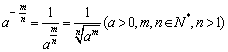
③ 练习:A.将下列根式写成分数指数幂形式:![]()
![]() ;
;![]() ;
;![]()
B. 求值 ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
④ 讨论:0的正分数指数幂? 0的负分数指数幂?
⑤ 指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.指数幂的运算性质:![]()
![]() ·
·![]() ;
; ![]() ;
; ![]() .
.
4. 教学例题:
① 出示例1. 求值:![]() ;
; ![]() ;
;
![]() ;
; ![]()
② 出示例2. 用分数指数幂的形式表示下列各式![]() :
:![]() ;
; ![]() ;
;![]() ;
;
③ 出示例3. 计算(式中字母均正):![]() ;
;![]() .
.
④ 出示例4. 计算:![]()
![]() ,
, ![]()
![]() ;
; ![]()
⑤ 讨论:![]() 的结果?→定义:无理指数幂.(结合教材P58利用逼近的思想理解无理指数幂意义)
的结果?→定义:无理指数幂.(结合教材P58利用逼近的思想理解无理指数幂意义)
无理数指数幂![]() 是一个确定的实数.实数指数幂的运算性质?
是一个确定的实数.实数指数幂的运算性质?
3. 小结:分数指数幂的意义,分数指数幂与根式的互化,有理指数幂的运算性质.
(三)、巩固练习:
① n为 时,![]() .
.
② 求下列各式的值:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
(四)、教学典型例题:
1. 化简:![]() .
.
2. 已知![]() ,试求
,试求![]() 的值.
的值.
3. 用根式表示![]() , 其中
, 其中![]() .
.
4. 已知x+x-1=3,求下列各式的值:![]()
5. 求值:![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
6. 已知![]() , 求
, 求![]() 的值.
的值.
7. 探究:![]() 时, 实数
时, 实数![]() 和整数
和整数![]() 所应满足的条件.
所应满足的条件.
(五)、巩固提高练习:
●★【题1】(2005年上海高考)方程![]() 的解是__________
的解是__________
●解答:![]()
★题2、(2003年上海20题12分)已知函数f(x)=,g(x)=;(1)、证明:函数f(x)为奇函数,并求出f(x)的单调区间;(2)、分别计算f(4)-5 f(2)g(2)和f(9)-5 f(3)g(3),并概括出涉及函数f(x)和g(x)的对所有不为0的实数x都成立的一个等式,并加以证明。
●解:单调↗为(-∞,0)和(0,+∞);(2)、f(4)-5 f(2)g(2)=f(9)-5 f(3)g(3)=0,一般地。有:f(x2)-5 f(x)g(x)=0.
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十三: 指数函数及其性质
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:
1、 使学生了解指数函数模型的实际背景,认识数学与现实生活及其他学科的联系;理解指数函数的的概念和意义,能画出具体指数函数的图象,掌握指数函数的性质.
2、 熟练掌握指数函数概念、图象、性质;掌握指数形式的函数定义域、值域,判断其单调性;培养学生数学应用意识![]()
二、教学重点:掌握指数函数的图象和性质.
三、教学难点:用数形结合的方法从具体到一般地探索、概括指数函数的性质.理解指数函数的简单应用模型.
四、教学过程:
(一)、复习提问:
①零指数幂:a0=_____(a≠0);②、负整数指数幂:a-p=_____( a≠0,p∈N*);④正分数指数幂:![]() =_____(a>0,m、n∈N*,n>1);⑤负分数指数幂:
=_____(a>0,m、n∈N*,n>1);⑤负分数指数幂:![]() =_____( a>0,m、n∈N*,n>1);
=_____( a>0,m、n∈N*,n>1);
(二)、讲授新课:
1.教学指数函数模型思想及指数函数概念:
① 探究两个实例:
●A.细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,第3次由4个分裂成8个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与次数x的函数关系式是什么?
◆B.一种放射性物质不断变化成其他物质,每经过一年的残留量是原来的84%,那么以时间x年为自变量,残留量y的函数关系式是什么?
② 讨论:上面的两个函数有什么共同特征?底数是什么?指数是什么?
③ 定义:一般地,函数![]() 叫做指数函数(exponential function),其中x是自变量,函数的定义域为R.
叫做指数函数(exponential function),其中x是自变量,函数的定义域为R.
④讨论:为什么规定![]() >0且
>0且![]() ≠1呢?否则会出现什么情况呢?→ 举例:生活中其它指数模型?
≠1呢?否则会出现什么情况呢?→ 举例:生活中其它指数模型?
2. 教学指数函数的图象和性质:
①、 作图:在同一坐标系中画出下列函数图象: ![]() ,
, ![]() (师生共作→小结作法)
(师生共作→小结作法)
②、 根据图象归纳:指数函数的性质 (书P56)
③、★ 出示P56:例6. 函数![]() (
(![]() )的图象经过点(3,
)的图象经过点(3,![]() ),求
),求![]() ,
,![]() ,
,![]() 的值.
的值.
④、★出示例7. 比较下列各组中两个值的大小:![]() ;
; ![]() ;
; ![]() ;
; ![]()
⑤、比较大小:![]() ;
;
(四)教学指数函数的应用模型:
①★ 出示例1:我国人口问题非常突出,在耕地面积只占世界7%的国土上,却养育着22%的世界人口.因此,中国的人口问题是公认的社会问题.2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%.为了有效地控制人口过快增长,实行计划生育成为我国一项基本国策.
(Ⅰ)按照上述材料中的1%的增长率,从2000年起,x年后我国的人口将达到2000年的多少倍?
(Ⅱ)从2000年起到2020年我国的人口将达到多少?
★ ② 练习: 2005年某镇工业总产值为100亿,计划今后每年平均增长率为8%, 经过x年后的总产值为原来的多少倍? → 变式:多少年后产值能达到120亿?
(五)、. 教学指数形式的函数定义域、值域:
◆1、①设y1=40.9,y2=80.48;y3=()-1.5,则三者的大小是_____y1>y3>y2
②设函数F(x)=[1+]·f(x)(且x≠0)是偶函数,又f(x)不恒等于0,则f(x)的奇偶性是_
(答案为:奇函数); ③函数y=1-2x,x∈[1,4]的值域为____[-15,-1]; ④、函数f(x)=()x+2,x∈[-1,2]的值域为____[,5];⑤函数y=a-x(a>0,a≠1)当a∈______时,它为↘ ,此时,当x∈___时,y<0 .答案:(1,+∞)Æ
⑥、已知函数f(x)=的定义域为(-∞,0)则a的取值范围是____(答案:0<a<1)
▲2.①、 一片树林中现有木材30000m3,如果每年增长5%,经过x年树林中有木材ym3,写出x,y间的函数关系式,并利用图象求约经过多少年,木材可以增加到40000m3
 ▲②、. 比较下列各组数的大小:
▲②、. 比较下列各组数的大小:
![]() ;
; ![]() .
.
▲3. 求函数![]() 的定义域和值域,并讨论函数的单调性、奇偶性.
的定义域和值域,并讨论函数的单调性、奇偶性.
【★题4】设a>1为常数,已知当x∈(-1,1)时,不等式x2-ax<![]() 恒成立,则a的取值范围为( A )
恒成立,则a的取值范围为( A )
A (1,2] B [2,+∞) C (1,4] D [4,+∞)
【★题5】已知函数¦(x)=ax –b的图象如图所示,其中a,b为常数,则下列结论正确的是( B )
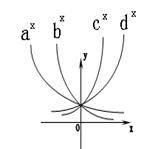 A a>1 b<0 B 0<a<1 b<0 C a>1 b>0 D 0<a<1,b>0
A a>1 b<0 B 0<a<1 b<0 C a>1 b>0 D 0<a<1,b>0
【★题6】指数函数y=ax,y=bx,y=cx,y=dx 在同一坐标系中的图象如下图所示,则a、b、c、d的大小顺序为( A )
A b<a<d<c B a<b<d<c C b<a<c<d D b<c<a<d
★【题7】已知实数a, b满足等式![]() 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有( B ) A.1个 B.2个 C.3个 D.4个
●【解答】![]() 均大于零时,要满足等式,必有
均大于零时,要满足等式,必有![]() ;
;![]() 均小于零时,要满足等式,必有
均小于零时,要满足等式,必有![]() ;
;![]() 时,显然等式成立.因此不可能成立的关系式为③④,选B
时,显然等式成立.因此不可能成立的关系式为③④,选B
★【题8】设函数![]() ,求使
,求使![]() 的
的![]() 取值范围.答案:
取值范围.答案:![]()
★9.(天津卷)如果函数![]() 在区间
在区间![]() 上是增函数,那么实数
上是增函数,那么实数![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.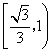 C.
C.![]() D.
D.![]()
●解析:函数y![]() 且
且![]() 可以看作是关于
可以看作是关于![]() 的二次函数,若a>1,则
的二次函数,若a>1,则![]() 是增函数,原函数在区间
是增函数,原函数在区间![]() 上是增函数,则要求对称轴
上是增函数,则要求对称轴![]() ≤0,矛盾;若0<a<1,则
≤0,矛盾;若0<a<1,则![]() 是减函数,原函数在区间
是减函数,原函数在区间![]() 上是增函数,则要求当
上是增函数,则要求当![]() (0<t<1)时,
(0<t<1)时,![]() 在t∈(0,1)上为减函数,即对称轴
在t∈(0,1)上为减函数,即对称轴![]() ≥1,∴
≥1,∴![]() ,∴实数
,∴实数![]() 的取值范围是
的取值范围是![]() ,选B.
,选B.
★10、(04年湖南文科)若直线y=2a与函数y=ax-1(a>0,且a≠1)的图象有两个公共点,则a的取值范围是_______.(0,)
★11、已知f(x)=,求f()+f()+f()+…+f()之值。(答案:500)
★12、已知f(x)= +,求证:f(x)为奇函数。
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十四:对数与对数运算(两课时)
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:理解对数的概念;能够说明对数与指数的关系;掌握对数式与指数式的相互转化.
二、教学重点:掌握对数式与指数式的相互转化.
三、教学难点:对数概念的理解.
四、教学过程:
(一)、复习准备:
★1.问题1:庄子:一尺之棰,日取其半,万世不竭![]() (1)取4次,还有多长?(2)取多少次,还有0.125尺?
(得到:
(1)取4次,还有多长?(2)取多少次,还有0.125尺?
(得到:![]() =?,
=?,![]() =0.125
=0.125![]() x=?)
x=?)
★2.问题2:假设2002年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产 是2002年的2倍? ( 得到:![]() =2
=2![]() x=? )
x=? )
▲问题共性:已知底数和幂的值,求指数![]() 怎样求呢?例如:课本实例由
怎样求呢?例如:课本实例由![]() 求x
求x
(二)、讲授新课:
1. 教学对数的概念:
① 定义:一般地,如果![]()
![]() ,那么数 x叫做以a为底 N的对数(logarithm).
,那么数 x叫做以a为底 N的对数(logarithm).
记作 ![]() ,其中a叫做对数的底数,N叫做真数
,其中a叫做对数的底数,N叫做真数![]()
② 定义:我们通常将以10为底的对数叫做常用对数(common logarithm),并把常用对数![]() 简记为lgN
简记为lgN![]() 在科学技术中常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数,并把自然对数
在科学技术中常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数,并把自然对数![]() 简记作lnN
简记作lnN![]() → 认识:lg5 ; lg3.5; ln10; ln3
→ 认识:lg5 ; lg3.5; ln10; ln3
③ 讨论:指数与对数间的关系 (![]() 时,
时,![]()
![]()
![]() )
)
| 式子 名称 | a | b | N |
| 指数式ab=N | 底数 | 指数 | 幂 |
| 对数式logaN=b | 底数 | 对数 | 真数 |
负数与零是否有对数? (原因:在指数式中
N
> 0 )![]() ,
, ![]()
2. 教学指数式与对数式的互化:
★① 出示P63:例1. 将下列指数式写成对数式:![]() ;
;![]() ;
;![]() ;
; ![]()
★② 出示例2. 将下列对数式写成指数式:![]() ; lg0.001=-3; ln100=4.606
; lg0.001=-3; ln100=4.606
(学生试练 → 订正 →
变式:![]() lg0.001=? )
lg0.001=? )
★③ 出示例3. 求下列各式中x的值:
![]() ;
; ![]() ;
; ![]() ;
; ![]()
(讨论:解方程的依据? → 试求 → 小结:应用指对互化求x)
★④
练习:求下列各式的值: ![]() ;
;
![]() ;
;
![]() 10000
10000
★⑤ 探究:![]()
![]()
3. 小结:对数概念;lgN与lnN;指数与对数的互化; 如何求对数值
三、巩固练习:
1. 练习:课本64页练习1、2、3、4题
2.计算: ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
; ![]() .
.
3. 作业:书P74:1、2、3、4题
第二课时: 2.2.1对数与对数运算(二)
一、教学要求: 掌握对数的运算性质,并能理解推导这些法则的依据和过程;能较熟练地运用法则解决问题.
二、教学重点:运用对数运算性质解决问题![]()
三、教学难点:对数运算性质的证明方法
四、教学过程:
(一)、复习准备:
1.
提问:对数是如何定义的? → 指数式与对数式的互化:![]()
![]()
![]()
2. 提问:指数幂的运算性质?
(二)、讲授新课:
1. 教学对数运算性质及推导:
① 引例: 由![]() ,如何探讨
,如何探讨![]() 和
和![]() 、
、![]()
![]() 之间的关系?
之间的关系?
设![]() ,
, ![]() ,由对数的定义可得:M=
,由对数的定义可得:M=![]() ,N=
,N=![]()
![]() ∴MN=
∴MN=![]()
![]() =
=![]()
∴![]() MN=p+q,即得
MN=p+q,即得![]() MN=
MN=![]() M +
M + ![]() N
N![]()
② 探讨:根据上面的证明,能否得出以下式子?
如果 a > 0,a ¹ 1,M > 0, N > 0 ,则
![]() ;
; ![]() ;
; ![]()
③ 讨论:自然语言如何叙述三条性质? 性质的证明思路?(运用转化思想,先通过假设,将对数式化成指数式,并利用幂运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式![]() )
)
2.教学例题:
① 出示例1. 用![]() ,
, ![]() ,
, ![]() 表示下列各式:
表示下列各式:![]() ;
; ![]()
(学生讨论:如何运用对数运算性质? → 师生共练 → 小结:对数运算性质的运用)
② 出示例2. 计算:![]() ;
;![]() ;
;![]() ;lg
;lg![]()
③ 探究:根据对数的定义推导换底公式![]() (
(![]() ,且
,且![]() ;
;![]() ,且
,且![]() ;
;![]() ).
).
作用:化底 → 应用:2000年人口数13亿,年平均增长率1℅,多少年后可以达到18亿?
④ 练习:运用换底公式推导下列结论:![]() ;
;![]()
(三)、巩固练习:
1. 设![]() ,
,![]() ,试用
,试用![]() 、
、![]() 表示
表示![]() .
.
变式:已知lg2=0.3010,lg3=0.4771,求lg6、lg12、lg![]() 的值.
的值.
2. 计算:![]() ;
; ![]() ;
; ![]() .
.
3. 试求![]() 的值
的值
*4. 设![]() 、
、![]() 、
、![]() 为正数,且
为正数,且![]() ,求证:
,求证:![]()
5. 已知
![]() 3 = a,
3 = a, ![]() 7 = b, 用
a, b 表示
7 = b, 用
a, b 表示![]() 56
56
6. 问题:1995年我国人口总数是12亿,如果人口的年自然增长率控制在1.25℅,问哪一年我国人口总数将超过14亿? (答案:![]() →
→![]() →
→ ![]() )
)
(四)、实际应用练习:
★ 出示例5:(P66) 20世纪30年代,查尔斯.里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大. 这就是我们常说的里氏震级M,其计算公式为:![]() ,其中A是被测地震的最大振幅,
,其中A是被测地震的最大振幅,![]() 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差).
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差).
(Ⅰ)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.001, 计算这次地震的震级(精确到0.1);(Ⅱ)5级地震给人的振感已比较明显,计算7.6级地震最大振幅是5级地震最大振幅的多少倍?(精确到1)
●分析解答:读题摘要 → 数量关系 → 数量计算 → 如何利用对数知识?
③ 出示例6: 当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据些规律,人们获得了生物体碳14含量P与生物死亡年数t之间的关系.回答下列问题:(Ⅰ)求生物死亡t年后它机体内的碳14的含量P,并用函数的观点来解释P和t之间的关系,指出是我们所学过的何种函数?(Ⅱ)已知一生物体内碳14的残留量为P,试求该生物死亡的年数t,并用函数的观点来解释P和t之间的关系,指出是我们所学过的何种函数?(Ⅲ)长沙马王墓女尸出土时碳14的余含量约占原始量的76.7%,试推算古墓的年代?
●分析解答:读题摘要 → 寻找数量关系 → 强调数学应用思想
⑤探究训练:讨论展示并分析自己的结果,试分析归纳,能总结概括得出什么结论?
结论:P和t之间的对应关系是一一对应;P关于t的指数函数![]() ;
;
思考:t关于P的函数? (![]() )
)
2. 小结:初步建模思想(审题→设未知数→建立x与y之间的关系→); 用数学结果解释现象
(五)、课堂巩固练习:
1. 计算: ![]() ;
; ![]()
![]()
2. 我国的GDP年平均增长率保持为7.3%,约多少年后我国的GDP在1999年的基础上翻两翻?
(六)、学生作业:
◆1、如果在今后若干年内,我国的国民经济生产总值都在平均每年增长9%的水平,则要达到国民经济生产总值比1995年翻两番的年份大约是哪一年?
解:a(1+9%)x=4a,x= =≈16,即经过16年,即要到2011年我国国民经济生产总值比1995年翻两番。(计算时取lg2=0.3;lg109=2.04)
★【题2】(200 7年湖南· T1)、若![]() ,
,![]() ,则
,则![]() .答案为:3
.答案为:3
★【题3】函数![]() 的图象大致是( )
的图象大致是( )
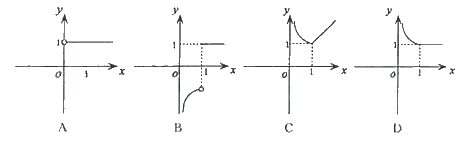
●解:![]() =
=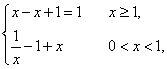 选(D)
选(D)
(七)、课堂回顾与总结:
对数及其运算的基本知识体系:
1、对数概念:若ab=N,⇔则有b=logaN (常用对数lgN,自然对数lnN)Þ负数和零没有对数。
2、对数的运算性质:(换底公式的应用):①loga1=0; ② logaa=1; ③![]() =_____; ④logab·logbc=____; ⑤ logab·logba=____; ⑥
=_____; ④logab·logbc=____; ⑤ logab·logba=____; ⑥![]() =___; ⑦loga(M·N)=____;
=___; ⑦loga(M·N)=____;
⑧loga()= _______; ⑨logaNb=____
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十五:对数函数及其性质(两课时)
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
课时一:
一、教学要求:通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型.能够用描点法画出对数函数的图象.能根据对数函数的图象和性质进行值的大小比较.培养学生数形结合的意识.用联系的观点分析问题.
二、教学重点:对数函数的图象和性质
三、教学难点:对数函数的图象和性质及应用
四、教学过程:
(一)、复习准备:
1、对数概念:若ab=N,⇔则有b=logaN (常用对数lgN,自然对数lnN)Þ负数和零没有对数。
2、对数的运算性质:(换底公式的应用):①loga1=0; ② logaa=1; ③![]() =_____; ④logab·logbc=____; ⑤ logab·logba=____; ⑥
=_____; ④logab·logbc=____; ⑤ logab·logba=____; ⑥![]() =___; ⑦loga(M·N)=____;
=___; ⑦loga(M·N)=____;
⑧loga()= _______; ⑨logaNb=____
(二)、讲授新课:
1.教学对数函数的图象和性质:
①
定义:一般地,当a>0且a≠1时,函数![]() 叫做对数函数(logarithmic function).
叫做对数函数(logarithmic function).
自变量是x; 函数的定义域是(0,+∞)
②
辨析: 对数函数定义与指数函数类似,都是形式定义,注意辨别,如:![]() ,
,![]() 都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制
都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制 ![]() ,且
,且![]() .
.
③ 探究:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
| 名称 | 指数函数 | 对数函数 |
| 一般解析式 | y=ax (a>0,a≠1) | y=logax (a>0,a≠1) |
| 定义域 | ||
| 值域 | ||
| 当a>1时的图像 | ①注意特殊点、单调性、变化范围等。 | ②同一坐标系中两个图像时底数的确定方法。 |
| 当0<a<1时的图像 | ||
| 两者的关系 | ||
2. 教学例题
① 出示P71:例7.求下列函数的定义域:![]() ;
; ![]() ;
; ![]()
② 出示P72:例8. 比较大小:![]() ;
;![]() ;
;![]()
课堂练习:P73:题1、2、3;P74:练习题:7、8、9
课时二:
一、教学要求:了解对数函数在生产实际中的简单应用.进一步理解对数函数图象和性质;学习反函数的概念,理解对数函数和指数函数互为反函数,能够在同一坐标上看出互为反函数的两个函数的图象性质.
二、教学重点与难点:理解反函数的概念
三、教学过程:
(一)、复习准备:
提问:对数函数![]() 的图象和性质?
的图象和性质?
(二)、讲授新课:
1. 教学对数函数模型思想及应用:
出示P72:例题9:溶液酸碱度的测量问题:溶液酸碱度pH的计算公式![]() ,其中
,其中![]() 表示溶液中氢离子的浓度,单位是摩尔/升. (Ⅰ)分析溶液酸碱读与溶液中氢离子浓度之间的关系?
(Ⅱ)纯净水
表示溶液中氢离子的浓度,单位是摩尔/升. (Ⅰ)分析溶液酸碱读与溶液中氢离子浓度之间的关系?
(Ⅱ)纯净水![]() 摩尔/升,计算纯净水的酸碱度.
摩尔/升,计算纯净水的酸碱度.
2.反函数的教学:
①、 分析:函数![]() 由
由![]() 解出,是把指数函数
解出,是把指数函数![]() 中的自变量与因变量对调位置而得出的. 习惯上我们通常用x表示自变量,y表示函数,即写为
中的自变量与因变量对调位置而得出的. 习惯上我们通常用x表示自变量,y表示函数,即写为![]() .那么我们就说指数函数
.那么我们就说指数函数![]() 与对数函数
与对数函数![]() 互为反函数
互为反函数
②、在同一平面直角坐标系中,画出指数函数![]() 及其反函数
及其反函数![]() 图象,发现什么性质?
图象,发现什么性质?
③、 探究:如果![]() 在函数
在函数![]() 的图象上,那么P0关于直线
的图象上,那么P0关于直线![]() 的对称点在函数
的对称点在函数![]() 图象上吗,为什么?由上述过程可以得到什么结论?(互为反函数的两个函数的图象关于直线
图象上吗,为什么?由上述过程可以得到什么结论?(互为反函数的两个函数的图象关于直线![]() 对称)
对称)
(三)、巩固练习:
1.求下列函数的反函数: y=![]() (x∈R); y=
(x∈R); y=![]()
![]() (a>0,a≠1,x>0)
(a>0,a≠1,x>0)
2.己知函数![]() 的图象过点(1,3)其反函数
的图象过点(1,3)其反函数![]() 的图象过(2,0)点,求
的图象过(2,0)点,求![]() 的表达式.
的表达式.
(四)、提高练习:
★1题.(1)证明函数![]() 在
在![]() 上是增函数(可利用复合函数法去处理)。(2)、探究:函数
上是增函数(可利用复合函数法去处理)。(2)、探究:函数![]() 在
在![]() 上是减函数还是增函数?(可利用偶函数的性质去处理)。
上是减函数还是增函数?(可利用偶函数的性质去处理)。
2. 求函数![]() 的单调区间.(强调:复合函数的单调性:同增异减,注意利用图象处理)
的单调区间.(强调:复合函数的单调性:同增异减,注意利用图象处理)
(五)、巩固补充练习
1.比较大小:![]() ;
;![]()
2.已知![]() 恒为正数,求
恒为正数,求![]() 的取值范围.
的取值范围.
3.求函数![]() 的定义域及值域.
的定义域及值域.
4.函数![]() 在[2,4]上的最大值比最小值大1,求
在[2,4]上的最大值比最小值大1,求![]() 的值;
的值;
5. 求函数![]() 的最小值.
的最小值.
6. 求下列函数的反函数:
![]() ;
; ![]() ;
; ![]() ;
; ![]()
(六)、课后提高作业
1.求![]() 的单调递增区间;
的单调递增区间;
2.已知![]() 在[0,1]上是
在[0,1]上是![]() 的减函数,求
的减函数,求![]() 的取值范围
的取值范围
(七)相关高考题摘录(供课时选择之用):
★【例题1】函数![]() 的定义域为( A
)
的定义域为( A
)
A.(1,2)∪(2,3)B.![]() C.(1,3)D.[1,3]
C.(1,3)D.[1,3]
【★题3】函数¦(x)=的定义域为____({x1<x≤2})
【★题4】函数y= 的单调递增区间为___([2,6)注意6是达不到的)
【★题5】函数y=lg(mx2-4mx+m+3);①当定义域为R时,求m的取值范围; ②当值域为R时,求m的取值范围。 解、①{m0≤m<1} ②{mm≥1 或m<0}
【★题8】解不等式log2(-x)<x+3的解集为( D )
A (-∞,-1) B (-∞,-2) C (-1,0) D (-2,0)
★【例题9】设![]() 则( )
则( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
 解:
解:![]() 则
则![]() ,选A.
,选A.
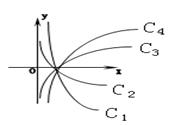
※ 【★题11】如图中的曲线是对数函数y=logax 的图象,已知a取, , ,四个值,则相应于曲线c1,c2,c3,c4 的a之值依次为_________
※
【★题12】设a>0,a≠1,函数¦(x)=![]() ,g(x)=1+loga(x-1)
,g(x)=1+loga(x-1)
① 求 ¦(x) 和 g(x)的定义域的公共部分D,并判定¦(x)在D内的单调性;若[m,n]ÜD,且¦(x)在[m,n]上的值域恰好为[g(n), g(m)],求a的取值范围
![]() 解、① >0
解、① >0
x-1>0 Þx>3 则D={xx>3};②当0<a<1时, ¦(x)为↘;当a>1时, ¦(x)为↗
③由g(n)< g(m)则loga(n-1)< loga(m-1) 而m<n,则0<a<1,故¦(x)为↘
则¦(n)= g(n), ¦(m)= g(m)其中3<m<n,故方程¦(x)= g(x)有两个大于3的不同实根,⇔ ![]() =1+loga(x-1)有大于3的两个实根⇔方程ax2+(2a-1)x+3(1-a)=0有两个大于3的实根⇔
=1+loga(x-1)有大于3的两个实根⇔方程ax2+(2a-1)x+3(1-a)=0有两个大于3的实根⇔
△
![]() >0
>0
>3
0<a<1
a·32+(2a-1)·3+3(1-a)>0 ∴0<a<为所求
(七)、课后巩固练习(供选择之用):
★【题1】已知![]() ,则( D )
,则( D )
(A) n<m < 1 (B) m<n< 1 (C) 1< m<n (D) 1 <n<m
★【题2】设f(x)=![]() ,则
,则![]() 的定义域为(B)
的定义域为(B)
A. ![]() B.(-4,-1)
B.(-4,-1)![]() (1,4) C. (-2,-1)
(1,4) C. (-2,-1)![]() (1,2) D. (-4,-2)
(1,2) D. (-4,-2)![]() (2,4)
(2,4)
★【题5】方程![]() 的解为
的解为![]() .
.
解:![]() Û
Û![]() ;即
;即![]() 解得
解得![]() (负值舍去)
(负值舍去)
★【题7】 函数![]()
![]() 的反函数是( D
)
的反函数是( D
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知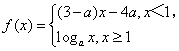 是(-
是(-![]() ,+
,+![]() )上的增函数,那么a的取值范围是
)上的增函数,那么a的取值范围是
(A)(1,+![]() ) (B)(-
) (B)(-![]() ,3) (C)[
,3) (C)[![]() ,3) (D)(1,3)
,3) (D)(1,3)
解:依题意,有a>1且3-a>0,解得1<a<3,又当x<1时,(3-a)x-4a<3-5a,当x³1时,logax³0,所以3-5a£0解得a³![]() ,所以1<a<3故选D
,所以1<a<3故选D
9.(福建卷)已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]()
![]() 则(A)
则(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]() ,
,![]() ,
,![]() <0,∴
<0,∴![]() ,选D.
,选D.
11.(辽宁卷)与方程![]() 的曲线关于直线
的曲线关于直线![]() 对称的曲线的方程为
对称的曲线的方程为
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
解:![]() ,
,![]() ,即:
,即:![]() ,所以
,所以![]() ,故选择答案A。
,故选择答案A。
12.(全国卷I)已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则
A、![]() B、
B、![]() C、
C、![]() D.
D.![]()
解:函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,所以
对称,所以![]() 是
是![]() 的反函数,即
的反函数,即![]() =
=![]() ,∴
,∴ ![]() ,选D.
,选D.
13.(全国II)函数y=f(x)的图像与函数g(x)=log2x(x>0)的图像关于原点对称,则f(x)的表达式为
(A) f(x)=(x>0) (B ) f(x)=log2(-x)(x<0) (C) f(x)=-log2x(x>0) (D) f(x)=-log2(-x)(x<0)
解析:(x,y)关于原点的对称点为(-x,-y),所以![]()
![]()
![]() 选D
选D
本题主要考察对称的性质和对数的相关性质,比较简单,但是容易把![]() 与
与![]() 搞混,其实
搞混,其实![]()
14.(山东卷)设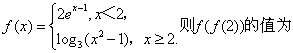 (A)0 (B)1
(C)2
(D)3
(A)0 (B)1
(C)2
(D)3
解:f(f(2))=f(1)=2,选C
15.(陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于( )A.6 B.5 C.4 D.3
解析:函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),
则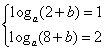 ,∴
,∴![]() ,
,![]() 或
或![]() (舍),b=1,∴a+b=4,选C.
(舍),b=1,∴a+b=4,选C.
20.(辽宁卷)设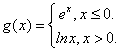 则
则![]() __________【解析】
__________【解析】![]() .
.
21.(辽宁卷)方程![]() 的解为 ________
的解为 ________
解:![]() Û
Û![]() ,即
,即![]() 解得
解得![]() (负值舍去),所以
(负值舍去),所以![]() 。
。
22.(上海卷)若函数![]() =
=![]() (
(![]() >0,且
>0,且![]() ≠1)的反函数的图像过点(2,-1),则
≠1)的反函数的图像过点(2,-1),则![]() = .
= .
解:由互为反函数关系知,![]() 过点
过点![]() ,代入得:
,代入得:![]() ;
;
23.(上海卷)方程![]() 的解是_______.
的解是_______.
解:方程![]() 的解满足
的解满足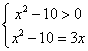 ,解得x=5.
,解得x=5.
25.(重庆卷)设![]() ,函数
,函数![]() 有最小值,则不等式
有最小值,则不等式![]() 的解集为
。
的解集为
。
解:由![]() ,函数
,函数![]() 有最小值可知a>1,所以不等式
有最小值可知a>1,所以不等式![]() 可化为x-1>1,即x>2.
可化为x-1>1,即x>2.
26.(上海春)方程![]() 的解
的解![]() .
.
解:由log3(2x-1),化为同底数的对数,得log3(2x-1)=log33,2x-1=3 ,即 x=2 .从而应填2.
27、(04年湖南文科)若直线y=2a与函数y=ax-1(a>0,且a≠1)的图象有两个公共点,则a的取值范围是_______.(0,1/2)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十六: 幂函数
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:通过具体实例了解幂函数的图象和性质,体会幂函数的变化规律及蕴含其中的对称性并能进行简单的应用.
二、教学重点:从五个具体幂函数中认识幂函数的一些性质.
三、教学难点:画五个幂函数的图象并由图象概括其性质.
四、教学过程:
(一)、新课引入:
◆实例分析:见书本P77五个实例:
(二)、讲授新课:
1、教学幂函数的图象与性质
■① 给出定义:一般地,形如![]()
![]() 的函数称为幂函数,其中
的函数称为幂函数,其中![]() 为常数.
为常数.
■②练:在函数![]() 中,哪几个函数是幂函数?(书本P79:习题第1题)
中,哪几个函数是幂函数?(书本P79:习题第1题)
■③ 作出下列函数的图象:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5).
;(5).![]()
▲ ④
引导学生观察图象,归纳概括幂函数的的性质及图象变化规律:
④
引导学生观察图象,归纳概括幂函数的的性质及图象变化规律:
(Ⅰ)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
(Ⅱ)![]() 时,幂函数的图象通过原点,并且在区间
时,幂函数的图象通过原点,并且在区间![]() 上是增函数.特别地,当
上是增函数.特别地,当![]() 时,幂函数的图象下凸(称为凸函数);当
时,幂函数的图象下凸(称为凸函数);当![]() 时,幂函数的图象上凸(称为凹函数);
时,幂函数的图象上凸(称为凹函数);
(Ⅲ)![]() 时,幂函数的图象在区间
时,幂函数的图象在区间![]() 上是减函数.在第一象限内,当
上是减函数.在第一象限内,当![]() 从右边趋向原点时,图象在
从右边趋向原点时,图象在![]() 轴右方无限地逼近
轴右方无限地逼近![]() 轴正半轴,当
轴正半轴,当![]() 趋于
趋于![]() 时,图象在
时,图象在![]() 轴上方无限地逼近
轴上方无限地逼近![]() 轴正半轴.
轴正半轴.
2、教学例题:
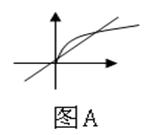
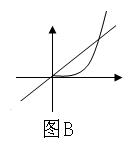 ★出示P78:书本之例1:讨论
★出示P78:书本之例1:讨论![]() 在
在![]() 的单调性.
的单调性.
◆3、小结:幂函数y=xa=xq/p的的性质及图象变化规律可以分为以下几类:
★1、直线类:y=x0,y=x
★2、抛物线类:y=x2,y=![]() ,y=
,y=![]() ……(即q是偶数,p是奇数,a=大于零)
……(即q是偶数,p是奇数,a=大于零)
性质有;(1)、必过点(0,0)、(1,1)、(-1,1);(2)定义域为R,且在(0,+∞)上为增函数,为偶函数;
(3)在第一象限内:当0<a<1时:为图(A)所示形式(上凸,称为凹函数);当a>1时:如图B所示(下凸,称为凸函数)
★3、拐线类:y=x3,y= y=![]() ,y= y=
,y= y=![]() ,y y=
,y y=![]() ……(即q是奇数,p是奇数,a=大于零);性质有;(1)、必过点(0,0)、(1,1)、(-1,-1);
……(即q是奇数,p是奇数,a=大于零);性质有;(1)、必过点(0,0)、(1,1)、(-1,-1);
(2)定义域为R,在(0,+∞)上为增函数,为奇函数;(3)在第一象限内:当0<a<1时:为图(A)所示形式(上凸,称为凹函数);当a>1时:如图B所示(下凸,称为凸函数)
★4、双曲线类:y=x-1,y=x-3,……(即p为奇数,且a=q/p<0时) ……性质有;(1)、必过点(1,1);(2)定义域为{xx≠0},在(0,+∞)上为减函数;
★5、半支抛物线类:y= y=![]() ;y= y=
;y= y=![]() …(即p为偶数,且a=q/p>0时)图象过点(0,0)、(1,1);定义域为{xx>0};图象只位于第一象限之内,且为增函数;
…(即p为偶数,且a=q/p>0时)图象过点(0,0)、(1,1);定义域为{xx>0};图象只位于第一象限之内,且为增函数;
而y= y=![]() , y=
, y=![]() …(即p为偶数,且a= <0时): 图象过点(1,1)定义域为{xx>0};图象只位于第一象限之内,且为减函数。
…(即p为偶数,且a= <0时): 图象过点(1,1)定义域为{xx>0};图象只位于第一象限之内,且为减函数。
总之:当a>0时,幂函数y=xa为增函数,当a<0时,幂函数y=xa为减函数。
(三)、练习及其应用
1、学法大视野:P26:求幂函数的解析式的基本方法:
例:幂函数y=f(x)的图象过点(3,),求出其解析式。(y= y=![]() )
)
2. 讨论函数![]() 的定义域、奇偶性,作出它的图象,并根据图象说明函数的单调性.
的定义域、奇偶性,作出它的图象,并根据图象说明函数的单调性.
3.利用幂函数的图象的特征解题:±2、±
4、利用幂函数的单调性比较幂的大小: ![]() 与
与![]() ;
;![]() 与
与![]() ;
;![]() 与
与![]() .
.
5、用数形结合的思想,求参数的取值范围:![]() <
< ![]() 求a的取值范围。(a∈(-∞,-2)∪(,)
求a的取值范围。(a∈(-∞,-2)∪(,)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十七:基本初等函数的归纳与概括应用
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:掌握指数函数、对数函数的概念,会作指数函数、对数函数的图象,并能根据图象说出指数函数、对数函数的性质,了解五个幂函数的图象及性质.
二、教学重点:指数函数、对数函数、幂函数的图象和性质.
三、教学难点:指数函数、对数函数、幂函数性质的简单应用.
四、教学过程:
(一)、复习归纳:
1. 提问:指数函数、对数函数、幂函数的图象和性质(比较一次函数、二次函数、反比例函数)
|
| 指数函数y=ax(a>0,a≠1) | 对数函数y=logax(a>0,a≠1) | 幂函数y=xa |
| 函数图象 | |||
| 定义域 | |||
| 值域 | |||
| 单调性 | |||
| 奇偶性 | |||
| 特殊点、线 |
2. 求下列函数的定义域:![]() ;
;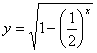 ;
;![]()
3. 比较下列各组中两个值的大小:![]() ;
;![]() ;
;![]()
二、典型例题:
例1、函数![]() 的定义域为_____________________.
的定义域为_____________________.
例2、函数![]() 的单调区间为_____________________.
的单调区间为_____________________.
例3、已知函数![]() .判断
.判断![]() 的奇偶性并予以证明.
的奇偶性并予以证明.
例4、按复利计算利息的一种储蓄,本金为![]() 元,每期利率为
元,每期利率为![]() ,设本利和为
,设本利和为![]() 元,存期为
元,存期为![]() ,写出本利和
,写出本利和![]() 随存期
随存期![]() 变化的函数解析式. 如果存入本金1000元,每期利率为2.25%,试计算5期后的本利和是多少(精确到1元)?(复利是一种计算利息的方法,即把前一期的利息和本金加在一起算做本金,再计算下一期的利息. )
变化的函数解析式. 如果存入本金1000元,每期利率为2.25%,试计算5期后的本利和是多少(精确到1元)?(复利是一种计算利息的方法,即把前一期的利息和本金加在一起算做本金,再计算下一期的利息. )
▲小结与要求:掌握指数函数、对数函数、幂函数的图象与性质,会用函数性质解决一些简单的应用问题. )
三、 巩固练习:
1.函数![]() 的定义域为________,值域为__________.
的定义域为________,值域为__________.
2. 函数![]() 的单调区间为__________________.
的单调区间为__________________.
3. 若点![]() 既在函数
既在函数![]() 的图象上,又在它的反函数的图象上,则
的图象上,又在它的反函数的图象上,则![]() =______,
=______,![]() =_______
=_______
4. 函数![]() (
(![]() ,且
,且![]() )的图象必经过点 .
)的图象必经过点 .
5. 计算![]() .
.
★【题6】. 求下列函数的值域:
![]() ;
; ![]() ;
; 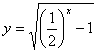 ;
; ![]()
●★【题7】设函数¦(![]() )= (x-x-1) 其中a>0且a≠1
)= (x-x-1) 其中a>0且a≠1
① 求¦(x)及其单调性和奇偶性;②当x∈(-1,1)时,¦(1-m)+¦(1-m2)<0恒成立,求m的取值范围;③当x∈(-∞,2)时, ¦(x)- 4的值恒为负数,求a的取值范围
◆ 解、①、¦(x)=(ax-a-x);
②、由复合函数法有:¦(x)为↗,由定义知¦(x)为奇函数; ③{m1<m<}④ 即考查¦(2)- 4 ≤0则{a2-≤a≤2+且a ≠1}
四、高考题选录:
★1.(北京卷)已知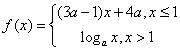 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
●解:依题意,有0<a<1且3a-1<0,解得0<a<![]() ,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³
,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³![]() 故选C
故选C
★2.(福建卷)已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]()
![]() 则
则
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
●解:已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]() ,
,![]() ,
,![]() <0,∴
<0,∴![]() ,选D.
,选D.
★3.(湖南卷)函数![]() 的定义域是( )
的定义域是( )
A.(3,+∞) B.[3, +∞) C.(4, +∞) D.[4, +∞)
●解:函数![]() 的定义域是
的定义域是![]() ,解得x≥4,选D.
,解得x≥4,选D.
★4.(陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于( )
A.6 B.5 C.4 D.3
●解析:函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),
则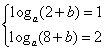 ,∴
,∴![]() ,
,![]() 或
或![]() (舍),b=1,∴a+b=4,选C.
(舍),b=1,∴a+b=4,选C.
★5.(重庆卷)已知定义域为![]() 的函数
的函数![]() 是奇函数。(Ⅰ)求
是奇函数。(Ⅰ)求![]() 的值;(Ⅱ)若对任意的
的值;(Ⅱ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
●解析:(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() =0,即
=0,即![]()
又由f(1)= -f(-1)知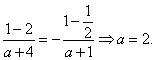
(Ⅱ)解法一:由(Ⅰ)知![]() ,易知
,易知![]() 在
在![]() 上
上
为减函数。又因![]() 是奇函数,从而不等式:
是奇函数,从而不等式: ![]()
等价于![]() ,因
,因![]() 为减函数,由上式推得:
为减函数,由上式推得:
![]() .即对一切
.即对一切![]() 有:
有:![]() ,从而判别式
,从而判别式![]()
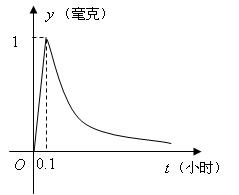 ★6、(07湖北)为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
★6、(07湖北)为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为![]() (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为 .
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室.
解: 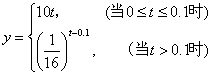 ;
; ![]()
★7、(07安徽)若![]()
![]() ,
,
则![]() 的元素个数为A.0 B.1 C.2 D.3 (C)
的元素个数为A.0 B.1 C.2 D.3 (C)
(07安徽)设a>1,且![]() ,则
,则![]() 的大小关系为( B )
的大小关系为( B )
(A) n>m>p (B) m>p>n (C) m>n>p (D) p>m>n
★8、(07重庆)若函数![]() 的定义域为R,则实数
的定义域为R,则实数![]() 的取值范围 。
的取值范围 。
![]()