高一数学数列测试题

高一数学数列测试题

　　　　　　　　　　　　  高一数学组　　　 2007.12

一、　　　  选择题（5分×10=50分）

1、4、三个正数a、b、c成等比数列，则lga、 lgb、 lgc是　　　 （　　 ）

A、等比数列　　　B、既是等差又是等比数列

 C、等差数列　　 D、既不是等差又不是等比数列　

2、前100个自然数中，除以7余数为2的所有数的和是（　　 ）

A、765　　B、653　 C、658　 D、660

3、如果a,x₁,x₂,b 成等差数列，a,y₁,y₂,b 成等比数列，那么(x₁+x₂)/y₁y₂等于　　　　　　　　　　　　　　　　 

A、(a+b)/(a-b)　　 B、(b-a)/ab　

C、ab/(a+b)　　　 D、(a+b)/ab

4、在等比数列{a_n}中，S_n表示前n项和，若a₃=2S₂+1,a₄=2S₃+1,则公比q=　　　　　　　　　　　　　　　　　　　 

A、1　　 B、-1　　 C、-3　　 D、3

5、在等比数列{a_n}中,a₁+a_n=66,a₂a_n-1=128,S_n=126，则n的值为　

A、5　　　 B、6　　　C、7　　　D、8

6、若{ a_n }为等比数列，S_n为前n项的和，S₃=3a₃,则公比q为　

A、1或-1/2　　B、-1 或1/2　 C、-1/2　 D、1/2或-1/2

7、一个项数为偶数的等差数列，其奇数项之和为24，偶数项之和为30，最后一项比第一项大21/2，则最后一项为　 （　　 ）

A、12　　　B、10　　C、8　　D、以上都不对

8、在等比数列{a_n}中，a_n>0,a₂a₄+a₃a₅+a₄a₆=25,那么a₃+a₅的值是

A、20　　B、15　　　C、10　　 D、5

9、等比数列前n项和为S_n有人算得S₁=8,S₂=20,S₃=36,S₄=65,后来发现有一个数算错了，错误的是　　　　　　　　

A、S₁　　 B、S₂　　 C、S₃　　D、S₄

10、数列{a_n}是公差不为0的等差数列，且a₇,a₁₀,a₁₅是一等比数列{b_n}的连续三项，若该等比数列的首项b₁=3则b_n等于　　

A、3·(5/3)^n-1　　　　B、3·(3/5)^n-1

C、3·(5/8)^n-1　　　　D、3·(2/3)^n-1

二、填空题（5分×5=25分）

11、公差不为0的等差数列的第2，3，6项依次构成一等比数列，该等比数列的公比=　　

12、各项都是正数的等比数列{a_n}，公比q1,a₅,a₇,a₈成等差数列，则公比q=　　　

13、已知a,b,a+b成等差数列,a,b,ab成等比数列，且0<log_mab<1，则实数m的取值范是　　

14、已知a _n=a_n－2+a _n－1(n≥3), a ₁=1,a₂=2, b _n=,则数列{b_n}的前四项依次是　　　　　　　　______________.

15、已知整数对的序列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），……，则第60个数对为　　　　

三、解答题（12分×4+13分+14=75分）
16、有四个数，前三个数成等比数列，其和为19，后三个数为等差数列，其和为12，求此四个数。

17、已知数列{a_n}的前n项和S_n=2n-n²,a_n=log₅bn ，其中bn>0，求数列{bn}的前n项和。

18．已知正项数列，其前项和满足且成等比数列，求数列的通项

19、在数列中，且，n.

错误！未找到引用源。求数列的通项公式。

错误！未找到引用源。设　　

20、已知数列的前n项和为，且满足，，

错误！未找到引用源。求证：数列是等差数列；错误！未找到引用源。求数列的通项公式。

21、在等差数列中，，。

(1) 求数列的通项公式；

(2) 令，求数列的前项和

答案

CADDB　 AADCA

3　 　 m>8　 　 (5,7)

规律：（1）两个数之和为n的整数对共有n-1个。（2）在两个数之和为n的n-1个整数对中，排列顺序为，第1个数由1起越来越大，第2个数由n-1起来越来越小。设两个数之和为2的数对方第1组，数对个数为1；两个数之和为3的数对为第二组，数对个数2;…… ,两个数之和为n+1的数对为第n组，数对个数为 n。

∵ 1+2+…+10=55，1+2+…+11=66

∴　第60个数对在第11组之中的第5个数，从而两数之和为12，应为（5，7）

16、25，—10，4，18或9，6，4，2

17、当n=1时，a₁=S₁=1

当n2时，a₁=S_n-S_n-1=3-2n　　 ∴a_n=3-2n　 b_n=5³-2n

∵　 b₁=5　　∴{b_n}是以5为首项，为公比的等比数列。

∴

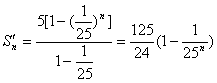
18、解: ∵10S_n=a_n²+5a_n+6, ①　 ∴10a₁=a₁²+5a₁+6,解之得a₁=2或a₁=3．

又10S_n－1=a_n－1²+5a_n－1+6(n≥2),②

由①－②得 10a_n=(a_n²－a_n－1²)+6(a_n－a_n－1),即(a_n+a_n－1)(a_n－a_n－1－5)=0　

∵a_n+a_n－1>0　, ∴a_n－a_n－1=5 (n≥2)．

当a₁=3时,a₃=13,a₁₅=73． a₁, a₃,a₁₅不成等比数列∴a₁≠3;

当a₁=2时, a₃=12, a₁₅=72, 有 a₃²=a₁a₁₅ , ∴a₁=2, ∴a_n=5n－3．

19、=10—2n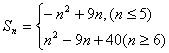　　　

20、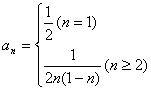

21、解：（1）设数列的公差为　 ∵　∴3

∴　　　　  ∴d=　　　　 ∴

(2)∴　　　　 ∴……①

∴………②

①　－②得：=

∴

21.(1)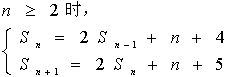

相减得：a_n+1=2a_n+1

故a_n+1+1=2（a_n+1）

又a₁+a₂=2a₁+6,解得a₂=11, a₂+1=2（a₁+1）

综上数列是等比数列.

(2)a_n=3∙2ⁿ-1