高一数学模块5水平监测试题
2008、04、23
| 卷一 | 卷二 | |||||||
| 题号 | 一 | 二 | 三 | 一 | 二 | 总分 | ||
| 15 | 16 | 17 | ||||||
| 分数 | ||||||||
卷一
一. 选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.
1. 在等差数列3, 7, 11 …中,第5项为( C )
A. 15 B.18 C.19 D.23
2. 数列
中, 如果
=3n（n=1, 2, 3, …） ，那么这个数列是（ C ）
A. 公差为2的等差数列 B. 公差为3的等差数列
C. 首项为3的等比数列 D. 首项为1的等比数列
3.等差数列中, 
, 那么它的公差是（ B ）
A. 4 B.5 C.6 D.7
4. △ABC中, ∠A，∠B，∠C所对的边分别为a, b, c.若
,∠C=
,
则c.的值等于（ C ）
A.
5
B. 13
C.
D.
5. 数列满足
（
）, 那么
的值为( C )
A. 4 B. 8 C. 15 D. 31
6. △ABC中, 如果
, 那么△ABC是（ B
）
A. 直角三角形 B. 等边三角形 C. 等腰直角三角形 D. 钝角三角形
7. 如果
, 设
, 那么（ A ）
A. 
B. 
C. 
D. M与N的大小关系随t的变化而变化
8. 如果为递增数列,则的通项公式可以为( D )
A. 
B. 
C. 
D. 
9. 如果
, 那么（ C ）
A.
B. 
C. 
D.
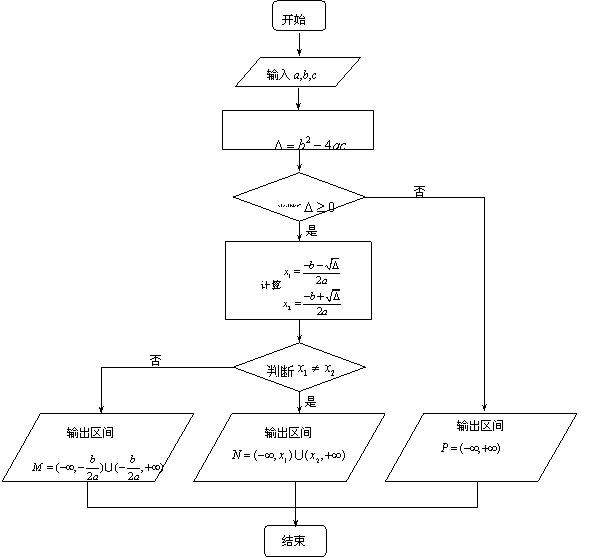
10.我们用以下程序框图来描述求解一元二次不等式ax2＋bx＋c>0(a>0)的过程.令a=2, b=4,若
，则输出区间的形式为（ B ）
A.M
B. N
C.P
D.
二. 填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
11.已知
是4和16的等差中项,则=___10___
12.一元二次不等式
的解集为__
___
13. 函数
的最大值为___
______
14. 在数列
中,其前
项和
,若数列是等比数列，则常数
的值为 -3
三.解答题.
15.三角形
中，
，且
.
（Ⅰ）求
；
（Ⅱ）求
.
解：（Ⅰ）由正弦定理得：
--------------------------6分
（Ⅱ）由余弦定理得：
,所以
。---------------12分
16.某工厂修建一个长方体形无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元。设池底长方形长为x米.
（Ⅰ）求底面积，并用含x的表达式表示池壁面积；
（Ⅱ）怎样设计水池能使总造价最低?最低造价是多少?
解：（Ⅰ）设水池的底面积为
，池壁面积为
,
则有
（平方米）,
可知，池底长方形宽为
米，则
--------------------------5分
（Ⅱ）设总造价为y，则
当且仅当
,即
时取等号,
所以时,总造价最低为297600元.
答：时,总造价最低为297600元.
--------------------------12分
17.已知等差数列的前n项的和记为
.如果
.
（Ⅰ）求数列的通项公式；
（Ⅱ）求Sn的最小值及其相应的n的值；
（Ⅲ）从数列中依次取出
,构成一个新的数列
,求的前n项和.
解：（Ⅰ）设公差为d，由题意，可得
，解得
，所以
-------------------------3分
（Ⅱ）由数列的通项公式可知，当
时，
，当
时，
，当
时，
。
所以当n＝9或n＝10时，取得最小值为
。-------------------------6分
（Ⅲ）记数列的前n项和为
，由题意可知
所以
-------------------------10分
卷二
一、填空题
1．在四个正数2，a，b，9中，若前三个数成等差数列，后三个数成等比数列，则a=____4_，b=___6___。
2．在△ABC中,
∠A，∠B，∠C所对的边分别为a, b, c，若
, 则
=_
__.
3．如果
，则
的最小值为 
。
4．如果有穷数列
（
，
）满足条件
即
，我们称其为“反对称数列”。
（1）请在下列横线上填入适当的数，使这6个数构成“反对称数列”：
－8， －4 ，－2， 2 ， 4 ， 8 ；
（2）设
是项数为30的“反对称数列”，其中
构成首项为-1，公比为2的等比数列.
设
是数列
的前n项和，则
= 
二、解答题
5．如图,在一建筑物底部B处和顶部A 处分别测得山顶C处的仰角为
和
（AB连线垂直于水平线），已知建筑物高AB=20米，求山高DC
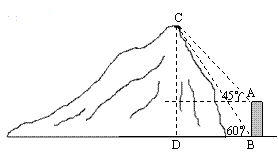
解：如图，在
中，由正弦定理可得
即 
所以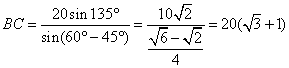
在
中，
所以山高为
米
法2
利用AE=DE列方程。
6．已知
为数列
的前
项和，且
（n=1,2,3…）.令
（n=1,2,3…）.
（Ⅰ）求证: 数列
为等比数列；
（Ⅱ）令
，记
，比较与
的大小。
（Ⅰ）解：
，
.
.
∴是以2为公比的等比数列
3分
（Ⅱ）
,
.
.
4分
=
=
×
+ 
×× 
＋…＋
××
= 
×(－) +×(－) ＋…＋×(－)
= ×(－)
= －
8分