高一数学五月段考题
2008-5-26
姓名__________ 学号_________ 分数___________
一.选择题 (每小题5分,共50分)
1. ![]()
A.第三象限角。 B.第四象限角。
![]()
2. 下列函数中,周期为![]() 的奇函数是
的奇函数是
A.![]() B.
B. ![]() C. y=sinx D. y=tan2x
C. y=sinx D. y=tan2x
3. 函数![]() 的图象的一条对称轴方程是
的图象的一条对称轴方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 设集合![]() ,则
,则
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5. 有下面四个命题:
①“x=2kπ+![]() (k∈Z)”是“tanx=
(k∈Z)”是“tanx=![]() ”的充分不必要条件;
”的充分不必要条件;
②函数f(x)=2cosx-1的最小正周期是π;
③函数f(x)=sin(x+![]() )在[
)在[![]() ,
,![]() ]上是增函数;
]上是增函数;
④若函数f(x)=asinx-bcosx的图象的一条对称轴的方程为x=![]() ,则a+b=0.
,则a+b=0.
其中正确命题的个数是
A.1 B.2 C.3 D.4
6. 若非零向量![]() 满足
满足![]() ,则
,则
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
7. 已知![]() ,
,![]() 是两个相互垂直的单位向量,而
是两个相互垂直的单位向量,而![]() ,
,![]() ,
,![]() 。则对于任意实数
。则对于任意实数![]() ,
,![]() 的最小值是
的最小值是
A.5 B.7 C.12 D.13
8. 设F(x)= f (x)+
f (-x),x∈R,[-π,-![]() ]是函数F(x)的单调递增区间,将F(x)的图象按向量a=(π,0)平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必是
]是函数F(x)的单调递增区间,将F(x)的图象按向量a=(π,0)平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必是
A.[-![]() ,0]
B.[
,0]
B.[![]() ,π] C.[π,
,π] C.[π,![]() ]
D.[
]
D.[![]() ,2π]
,2π]
9. 若=,=2,且(-)⊥,则与的夹角是
A. B. C. D.
10. 将函数![]() 的图象按向量
的图象按向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是
可以是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共5道填空题6道解答题)
请将你认为正确的答案代号填在下表中
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二.简答题 (每小题5分,共25分)
11. 已知空间四边形OABC,点M、N分别是边OA、BC的中点,![]()
12. 函数![]() 的最小正周期为__________,此函数的值域为__________
的最小正周期为__________,此函数的值域为__________
13. 函数![]() 的值域是________。
的值域是________。
14. 函数![]() 的最大值是________
的最大值是________
15. 在![]() 中,已知
中,已知![]() ,则
,则![]() 的面积
的面积![]() ___________.
___________.
三.解答题 (共75分)
16. 已知△ABC的三个内角分别为A,B,C,向量![]() 夹角的余弦角为
夹角的余弦角为![]()
(1)求角B的大小;
(2)求![]() 的取值范围.
的取值范围.
17. 已知△ABC内接于单位圆,且![]() ,
,
(1) 求证内角C为定值;
(2)求△ABC面积的最大值.
18. ![]()
其最小正周期为π.
(1)求实数a与ω的值.
(2)写出曲线y=f(x)的对称轴方程及其对称中心的坐标.
19. 在![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值和
的值和![]() 的面积.
的面积.
20. 已知函数![]()
(1)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
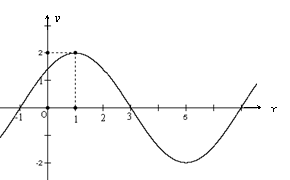
21. 已知函数![]() 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的最大值与最小值.
的最大值与最小值.
2008年武昌区高一数学五月段考题参考答案(仅供参考)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | B | B | B | B | C | C | D | B | D |
7. 由条件可得 ![]()
![]()
![]()
![]()
当![]() 时,
时,![]() 。
。![]() 选 【 C 】
选 【 C 】
8. ∵F(-x)=f(-x)+ f(x)=F(x),∴F(x)为偶函数.∴[![]() ,π]是F(x)的单调递减区间,按a平移后即得到G(x)的单调减区间.
,π]是F(x)的单调递减区间,按a平移后即得到G(x)的单调减区间.
二.简答题答案:
11. ![]()
12. ![]()
13. ![]() =2
=2![]()
=![]() =
=![]()
又![]() 且
且 ![]() 所以
所以![]()
14. ![]()
15. ![]() 或
或![]()
三.解答题答案:
16. (1)![]()
![]() ……………2分
……………2分
即![]()
![]()
解得![]() (舍)
(舍) ![]()
![]()
(2)由(1)可知![]()
![]() …… 9分
…… 9分
![]() ,
, ![]()
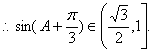
即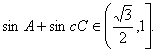
17. (1)由![]()
![]()
![]()
![]()
![]()
即![]() ,所以∠
,所以∠![]()
(2)由题意可得![]()
![]()
当AC=BC时,![]() 有最大值,最大值为
有最大值,最大值为![]()
![]()
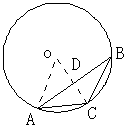
再作辅助线如图,连结OD,OA,得AB⊥OC,
所以AD=BD= ![]() ,CD=1-
,CD=1-![]() ,
,
AC2=AD2+CD2=
![]() 所以
所以![]() 最大值=
最大值=![]() =
= ![]()
18. ![]()
![]()
∵y的最小正周期T=π,∴ω=1
![]()
![]() .
.
![]() .
.
![]()
19. 解法一: ![]()
又![]() ,
,![]()
![]() .
.
![]()
解法二:![]() , (1)
, (1)![]()
![]()
![]() ,
,![]() , (2)
, (2)
(1)+(2)得:![]() ,(1)-(2)得:
,(1)-(2)得:![]() ,
,
![]() . (以下同解法一)
. (以下同解法一)
20. (1)![]()
![]() =
=![]()
![]() 的最小正周期
的最小正周期![]()
由题意得![]()
即 ![]()
![]() 的单调增区间为
的单调增区间为![]()
(II)方法一:
先把![]() 图象上所有点向左平移
图象上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象,再把所得图象上所有的点向上平移
的图象,再把所得图象上所有的点向上平移![]() 个单位长度,就得到
个单位长度,就得到![]() 的图象。
的图象。
方法二:
把![]() 图象上所有的点按向量
图象上所有的点按向量![]() 平移,就得到
平移,就得到![]() 的图象。
的图象。
21. (1)由图象A=2,周期T=8
![]()
![]()
又图象经过点(![]() 1,0)
1,0)![]()
![]() ………………6分
………………6分
(2)![]()
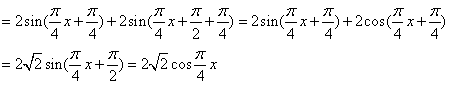
![]()
![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() 。
。