高一数学第一学期授课讲义
讲义十八:方程的根和函数的零点
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:
结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系;掌握零点存在的判定条件.
二、教学重点:体会函数的零点与方程根之间的联系,掌握零点存在的判定条件.
三、教学难点:恰当的使用信息工具,探讨函数零点个数.
四、教学过程:
(一)、复习准备:
※★思考:一元二次方程![]() +bx+c=o(a
+bx+c=o(a![]() 0)的根与二次函数y=ax
0)的根与二次函数y=ax![]() +bx+c的图象之间有什么关系?
+bx+c的图象之间有什么关系?
(二)、讲授新课:
1、探讨函数零点与方程的根的关系:
① 探讨:方程x![]() -2x-3=0 的根是什么?函数y= x
-2x-3=0 的根是什么?函数y= x![]() -2x-3的图象与x轴的交点?
-2x-3的图象与x轴的交点?
方程x![]() -2x+1=0的根是什么?函数y= x
-2x+1=0的根是什么?函数y= x![]() -2x+1的图象与x轴的交点?
-2x+1的图象与x轴的交点?
方程x![]() -2x+3=0的根是什么?函数y= x
-2x+3=0的根是什么?函数y= x![]() -2x+3的图象与x轴有几个交点?
-2x+3的图象与x轴有几个交点?
② 根据以上探讨,让学生自己归纳并发现得出结论: → 推广到y=f(x)呢?
一元二次方程![]() +bx+c=o(a
+bx+c=o(a![]() 0)的根就是相应二次函数y=ax
0)的根就是相应二次函数y=ax![]() +bx+c的图象与x轴交点横坐标.
+bx+c的图象与x轴交点横坐标.
③ 定义零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
④ 讨论:y=f(x)的零点、方程f(x)=0的实数根、函数y=f(x) 的图象与x轴交点的横坐标的关系?
■结论:方程f(x)=0有实数根![]() 函数y=f(x) 的图象与x轴有交点
函数y=f(x) 的图象与x轴有交点![]() 函数y=f(x)有零点
函数y=f(x)有零点
⑤ 练习:求下列函数的零点 ![]() ;
;![]() →
→
▲ 小结:二次函数零点情况(由一元二次次方程的判别式去确定)
 2、教学零点存在性定理及应用:
2、教学零点存在性定理及应用:
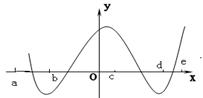
①、观察下面函数![]() 的图象,在区间
的图象,在区间![]() 上______(有/无)零点;
上______(有/无)零点;![]() ·
·![]() _____0(<或>). 在区间
_____0(<或>). 在区间![]() 上______(有/无)零点;
上______(有/无)零点;![]() ·
·![]() _____0(<或>). 在区间
_____0(<或>). 在区间![]() 上______(有/无)零点;
上______(有/无)零点;![]() ·
·![]() _____0(<或>).
_____0(<或>).
②、◆定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c![]() (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
④ 应用:书本例题1:(P88)求函数f(x)=Lnx+2x-6的零点的个数.(注意:如何证明该函数是严格的单调递增函数?) (试讨论一些函数值→分别用代数法、几何法)
⑤小结:函数零点的求法
■★代数法:求方程![]() 的实数根;
的实数根;
■★几何法:对于不能用求根公式的方程,可以将它与函数![]() 的图象联系起来,并利用函数的性质找出零点.
的图象联系起来,并利用函数的性质找出零点.
⑥ 练习:求函数![]() 的零点所在区间.
的零点所在区间.
3、小结:零点概念;零点、与x轴交点、方程的根的关系;零点存在性定理
三、巩固练习:1. P88: 1题、2题 (教师计算机演示,学生回答)
2. 求函数![]() 的零点所在区间,并画出它的大致图象.
的零点所在区间,并画出它的大致图象.
3. 求下列函数的零点:① 、![]() ; ②、
; ②、![]() ;
;
③、![]() ; ④、
; ④、![]() .
.
4. 已知![]() :
:
(1)![]() 为何值时,函数的图象与
为何值时,函数的图象与![]() 轴有两个零点;
轴有两个零点;
(2)如果函数至少有一个零点在原点右侧,求![]() 的值.
的值.
5. 作业:P92, 2题;P93: 3题
四、课堂教学巩固练习及学生作业:
●1、判断方程在区间(,8)上是否存在有实数解,并说明理由:log2x+3x-2=0
★解:∵f()<0,f(8)>0,且f(x)连续,则方程有实数解。)
●2、若方程ax2-x-1=0在(0,1)内有解,则实数a的取值范围是_____
★解:f(0)¦(1)<0,则a>2
●3、方程lgx+x=0的根所在区间是( B )
A (-∞,0) B (0,1) C (1,2) D (2,4)
●4、若函数¦(x)=x2-ax-b的两个零点是2和3,则函数g(x)=bx2-ax-1的零点是______,
● 5、已知二次函数¦(x)=x2-(m-1)x+2m在区间[0,1]上有且只有一个零点,求实数m的取值范围
★解:[-2,0])
●6.设函数![]() 则关于x的方程
则关于x的方程
![]() 解的个数为( C )
解的个数为( C )
A.1 B.2 C.3 D.4
● 7、使log2(-x)<x+1成立的x的取值范围是_____(-1,0)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十九:用二分法求方程的近似解
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:根据具体函数图象,能够借助计算器用二分法求相应方程的近似解. 通过用二分法求方程的近似解,使学生体会函数零点与方程根之间的联系,初步形成用函数观点处理问题的意识.
二、教学重点:用二分法求方程的近似解.
三、教学重点:恰当的使用信息工具.
四、教学过程:
(一)、复习准备:
★1. 提问:什么叫零点?零点的等价性? 零点存在性定理?
零点概念:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
方程f(x)=0有实数根![]() 函数y=f(x) 的图象与x轴有交点
函数y=f(x) 的图象与x轴有交点![]() 函数y=f(x)有零点
函数y=f(x)有零点
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c![]() (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
★2. 探究:一元二次方程求根公式? 三次方程? 四次方程?
材料:高次多项式方程公式解的探索史料:在十六世纪,已找到了三次和四次函数的求根公式,但对于高于4次的函数,类似的努力却一直没有成功,到了十九世纪,根据阿贝尔(Abel)和伽罗瓦(Galois)的研究,人们认识到高于4次的代数方程不存在求根公式,亦即,不存在用四则运算及根号表示的一般的公式解.同时,即使对于3次和4次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题
★3、生活实例:
●高沙至洞口的一条电话线路发生故障,请问如何去迅速查出故障之所在?
 ▲解:如果沿着线路一小段一小段去查找,困难很多;每查一次要爬一次电杆,10KM长的线路,大约有200多根电杆。
▲解:如果沿着线路一小段一小段去查找,困难很多;每查一次要爬一次电杆,10KM长的线路,大约有200多根电杆。
维修人员这样工作最合理:
①、先从中间位置板桥查起:若用随身所带的话机向两端测试,发现高沙到板桥段正常,则可确定板桥到洞口段有故障;
②、再从中间位置花古处查,若板桥到花古段正常,则可确定故障出花古到洞口段。——————每查一次,则可将线路缩短一半,当把故障可能发生的范围缩小到50m~100m左右时,即只有一至两根电线杆时,则只要查几次就够了。————这种检查线路故障的方法,不仅可用于查找线路、水管、气管等故障,还能用于实验设计、资料查询等,同时也是本节所学的求方程的近似解的二分法方法。
(二)、讲授新课:
1. 教学二分法的思想及步骤:
★① 出示例:有12个小球,质量均匀,只有一个是比别的球重的,你用天平称几次可以找出这个球的,要求次数越少越好. ( 让同学们自由发言,找出最好的办法)
◆解:第一次,两端各放六个球,低的那一端一定有重球;第二次,两端各放三个球,低的那一端一定有重球;第三次,两端各放一个球,如果平衡,剩下的就是重球,否则,低的就是重球.
其实这就是一种二分法的思想,那什么叫二分法呢?
② 探究:![]() 的零点所在区间?如何找出这个零点? → 师生用二分法探索
的零点所在区间?如何找出这个零点? → 师生用二分法探索
③ 定义二分法的概念:对于在区间[a,b]上连续不断且f(a).f(b)<0的函数y=f(x),通过不断的把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法(bisection)
④ 探究:给定精度ε,用二分法求函数![]() 的零点近似值的步骤如下:
的零点近似值的步骤如下:
A.确定区间![]() ,验证
,验证![]() ,给定精度ε;B. 求区间
,给定精度ε;B. 求区间![]() 的中点
的中点![]() ;
;
C. 计算![]() : 若
: 若![]() ,则
,则![]() 就是函数的零点; 若
就是函数的零点; 若![]() ,则令
,则令![]() (此时零点
(此时零点![]() ); 若
); 若![]() ,则令
,则令![]() (此时零点
(此时零点![]() );
);
D. 判断是否达到精度ε;即若![]() ,则得到零点值a(或b);否则重复步骤2~4.
,则得到零点值a(或b);否则重复步骤2~4.
2. 教学例题:
① 出示例:借助计算器或计算机用二分法求方程2![]() +3x=7的近似解. (师生共练)
+3x=7的近似解. (师生共练)
② 练习:求函数![]() 的一个正数零点(精确到
的一个正数零点(精确到![]() )
)
(三)、巩固练习:
★1、 设![]() , 用二分法求方程
, 用二分法求方程![]() 内近似解的过程中, 计算得到
内近似解的过程中, 计算得到![]() 则方程的根落在区间( B ).
则方程的根落在区间( B ).
A.(1,1.25) B.(1.25,1.5) C.(1.5,2) D.不能确定
★2.(2005年北京高考第20题·14分)
设![]() 是定义在[0,1]上的函数,若存在x*
是定义在[0,1]上的函数,若存在x*![]() 上单调递增,在[x*,1]上单调递减,则称
上单调递增,在[x*,1]上单调递减,则称![]() 为[0,1]上的单峰函数, x*为峰点,包含峰点的区间为含峰区间.
为[0,1]上的单峰函数, x*为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数![]() ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的![]() 为含峰区间;
为含峰区间;
若![]() 为含峰区间;
为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在![]() ,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取![]() ,由(Ⅰ)可确定含峰区间为(0,
,由(Ⅰ)可确定含峰区间为(0,![]() )或(
)或(![]() ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取![]() 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,![]() )的情况下,试确定
)的情况下,试确定![]() 的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34. (区间长度等于区间的右端点与左端点之差)
的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34. (区间长度等于区间的右端点与左端点之差)
●解:(I)证明:设x*为![]() 的峰点,则由单峰函数定义可知
的峰点,则由单峰函数定义可知![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 上单调递减. 当
上单调递减. 当![]() 时,假设
时,假设![]() ,则
,则![]() 从而
从而![]() 这与
这与![]() 矛盾,所以
矛盾,所以![]() ,即
,即![]() 是含峰区间.
是含峰区间.
当![]() 时,假设
时,假设![]() ,则
,则![]() ,从而
,从而![]() 这与
这与![]() 矛盾,所以
矛盾,所以![]() ,即
,即![]() 是含峰区间.
是含峰区间.
(II)证明:由(I)的结论可知: 当![]() 时,含峰区间的长度为
时,含峰区间的长度为![]() 当
当![]() 时,含峰区间的长度为
时,含峰区间的长度为![]() 对于上述两种情况,由题意得
对于上述两种情况,由题意得
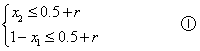
由①得![]() ,即
,即![]()
又因为![]() ,所以
,所以![]() ;
;
将②代入①得![]() ;
;
由①和③解得![]() 所以这时含峰区间的长度
所以这时含峰区间的长度![]() ,即存在
,即存在![]() 使得所确定的含峰区间的长度不大于
使得所确定的含峰区间的长度不大于![]()
(III)解:对先选择的![]() ,由(II)可知
,由(II)可知![]()
在第一次确定的含峰区间为![]() 的情况下,
的情况下, ![]() 的取值应满足
的取值应满足![]()
由④与⑤可得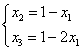 当
当![]() 时,含峰区间的长度为
时,含峰区间的长度为![]() 由条件
由条件![]() ,得
,得![]() ,从而
,从而![]()
因此,为了将含峰区间的长度缩短到![]() ,只要取
,只要取 ![]()
(四).课堂回顾与小结:
二分法的概念, 二分法的步骤;注重二分法思想
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义二十:函数与方程复习 ———— 《函数与方程》同步练习
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一. 选择题:
★1. 函数![]() 的零点为 ( A )
的零点为 ( A )
(A).1或3 (B).-1或3 (C).1或-3 (D).-1或-3
★2. 下列函数在区间[1,2]上有零点的是 ( D )
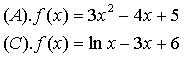
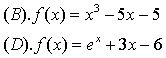
★3. 下列函数中有两个零点的是 ( D )
![]()
![]()
![]()
![]()
★4. 方程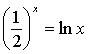 的根的个数为 ( B )
的根的个数为 ( B )
(A).0 (B).1 (C).2 (D).3
★5. 方程![]() 的解的个数是 ( D )
的解的个数是 ( D )
(A).0 (B).1 (C).2 (D).与a的取值有关
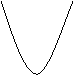
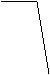
★6. 下列函数图象与x轴均有交点,其中不能用二分法求图中交点的横坐标的是( A )
![]()
![]()
![]()
![]()
 y
y
y
y
y
y
y
y
 | |||||
 |  | ||||
![]()
![]()
![]()
![]()
![]() 0 1
2 3 x 0 1 x 0 1 x
0 1 2 x
0 1
2 3 x 0 1 x 0 1 x
0 1 2 x
(A)![]()
![]() (B)
(C)
(D)
(B)
(C)
(D)
★7. 函数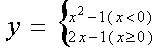 的零点为 ( C )
的零点为 ( C )
(A).![]() (B).
(B).
![]() (C).
(C). ![]() (D).
(D). ![]()
★8.如果函数![]() 在区间(-1,0)内存在零点,则a的取值可以是 ( D )
在区间(-1,0)内存在零点,则a的取值可以是 ( D )
(A)![]() (B)0
(C)
(B)0
(C) ![]() (D) –1
(D) –1
二. 填空题:
★9.函数![]() 在R上的零点有_____1个
在R上的零点有_____1个
★10.已知函数![]() ,若f(x)在R上有一个零点,a=__±2_____;若f(x)在R 上有2个零点,则a的取值范围为________{aa>2或a<-2}______.
,若f(x)在R上有一个零点,a=__±2_____;若f(x)在R 上有2个零点,则a的取值范围为________{aa>2或a<-2}______.
★11.方程![]() 有两个不等实根
有两个不等实根![]() ,且
,且![]() ,则实数k的取值范围为_______(0,
,则实数k的取值范围为_______(0,![]() );__.
);__.
★12.若函数![]() 有零点,则实数m的取值范围是____(0,1);_______.
有零点,则实数m的取值范围是____(0,1);_______.
★13.已知函数![]() 是R上的奇函数,则函数
是R上的奇函数,则函数![]() 的图象关于___原点____对称; 若
的图象关于___原点____对称; 若![]() 有2005个零点(记为
有2005个零点(记为![]() ),则
),则![]() ___0_.
___0_.
三. 解答题:
★14. 已知函数![]() ,判断方程
,判断方程![]() 在区间[1,1.5]内是否有实数解,如果有,求出一个近似解(精确到0.1). (答案为1.3)
在区间[1,1.5]内是否有实数解,如果有,求出一个近似解(精确到0.1). (答案为1.3)
★15.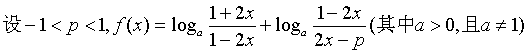
(1)
求![]() 的定义域;(2)、求证:函数
的定义域;(2)、求证:函数![]() 无零点.
无零点.
●解:(1){x![]() <x<
<x<![]() }; (2)反证法.
}; (2)反证法.
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义二十一:几类不同增长的函数模型及时其应用(1)
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:
①、结合实例体会直线上升,指数爆炸,对数增长等不同增长的函数模型的意义.
②、借助信息技术,利用函数图象及数据表格,比较指数函数、对数函数以及幂函数的增长差异.
③、恰当运用函数的三种表示法(解析式、图象、表格)并借助信息技术解决一些实际问题.
④、收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数、分段函数等),了解函数模型的广泛应用.
二、教学重点:
将实际问题转化为函数模型,比较常数函数、一次函数、指数函数、对数函数模型的增长差异,结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义.
三、教学难点:怎样选择数学模型分析解决实际问题.
四、教学过程:
(一)、新课引入:
国际象棋棋盘的奖赏→教科书第三章的章头图:澳大利亚兔子数“爆炸”。
有一大群喝水、嬉戏的兔子,但是这群兔子曾使澳大利亚伤透了脑筋.1859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,不到100年,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了相当于75亿只羊所吃的牧草,草原的载畜率大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.
(二)、讲授新课:
1、例题讲解:
★① 书本P95面例1.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天翻一番.请问,你会选择哪种投资方案?
② 探究:在本例中涉及哪些数量关系?如何用函数描述这些数量关系?→师生共同分析解答
探究:根据例1的数据,你对三种方案分别表现出的回报资金的增长差异有什么认识?
借助计算器或计算机作出函数图象,并通过图象描述一下三种方案的特点吗?
根据以上分析,你认为就作出如何选择?
★③书本P97: 例2. 某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金![]() (单位:万元)随销售利润
(单位:万元)随销售利润![]() (单位:万元)的增加而增加但奖金不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
(单位:万元)的增加而增加但奖金不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:![]() ;
;![]() ;
;![]() . 问:其中哪个模型能符合公司的要求?
. 问:其中哪个模型能符合公司的要求?
④ 探究:本例涉及了哪几类函数模型?本例的实质是什么?
根据问题中的数据,如何判定所给的奖励模型是否符合公司要求?
通过对三个函数模型增长差异的比较,写出例2的解答.
2、探究与发现: 幂函数、指数函数、对数函数的增长差异分析:当自变量变得很大时,指数函数比一次函数增长得快,一次函数比对数函数增长得快。
你能否仿照前面例题使用的方法,探索研究幂函数![]() 、指数函数
、指数函数![]() 、对数函数
、对数函数![]() 在区间
在区间![]() 上的增长差异:
上的增长差异:
在区间(0,+∞)上,尽管函数y=ax(a>1)、y=logax(a>1)、y=xn(n>0)都是增函数,但它们的增长速度是不相同的,而且不在同一个“档次”上。随着x的增大,y=ax(a>1)的增长速度会越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢,因此总会存在一个x0,当x>x0时,就有logax<xn<ax。
3、尝试练习: 教材P110练习1、2; 教材P113练习.
4、小结与反思:直线上升、指数爆炸、对数增长等不同函数模型的增长的含义;数学的实用性
(三)、巩固练习:
★1、令人目瞪口呆的“指数爆炸”:
王先生从今天开始每天给你10万元,而你则第一天给王先生1元,第二天给王先生2元,第三天给王先生4元,第四天给王先生8元……第n天给王先生2n-1元;
①、若王先生要与你签订15天的合同,你同意吗?
②、若王先生要与你签订30天的合同,你认为怎样呢?(可用公式有:20+21+22+23+24+…+2n-1=)
◆解:①、S1=215-1=32767(元)< 150(万元),可以接受;
②、S2=230-1=(元)>300(万元),无法接受。
★2、以下四种说法中,正确的是( D )
A、对任意的x>0,xa>logax(0<a<1) B、对任意的x>0,xa>logax(a>1)
C、对任意的x>0,ax>logax D、一定存在有x0,使得当x>x0时,总有ax>xn>logax成立。
(四)、常见的函数模型:
①、一次函数型模型:y=kx+b(k、b为常数,且k≠0)
②、二次函数型模型:y=ax2+bx+c(a、b、c为常数,且a≠0)
③、指数函数型模型:y=abx+c(a、b、c为常数,且a≠0,b>0,b≠1)
④、对数函数型模型:y=mlogax+n(m、n、a为常数,且a>0,a≠1)
⑤、幂函数型模型:y=axn+b(a、b、n为常数,且a≠0,n≠1)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义二十二:几类不同增长的函数模型(2)
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、教学要求:通过一些实例,来感受一次函数、二次函数、指数函数、对数函数以及幂函数的广泛应用,体会解决实际问题中建立函数模型的过程,从而进一步加深对这些函数的理解与应用.
二、教学重点:建立函数模型的过程.
三、教学难点:在实际问题中建立函数模型.
四、教学过程:
(一)、新课引入:前节课主要是讲授指数函数、对数函数以及幂函数的增长差异,本节课我们主要是通过一些生活中常遇到的实例来进一步说明函数模型在解决实际问题中的应用.
(二)、讲授新课:
1、例题讲解:
① 、★例1、在中国轻纺城批发市场,季节性服装当季节即将来临时,价格呈上升趋势. 设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周降价2元,直到16周末,该服装已不再销售.
(1)试建立价格P与周次t之间的函数关系;
(2)若此服装每件进价Q与周次t之间的关系式为![]() ,试问该服装第几周每件销售利润最大?
,试问该服装第几周每件销售利润最大?
(找出实际问题中涉及的函数变量→引导学生根据变量间的关系建立函数模型→利用模型解决实际问题→小结:二次函数模型)
②练习(图表形式):某同学完成一项任务共花去9个小时,他记录的完成工作量的百分数如下:
| 时间/小时 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 完成的百分数 | 15 | 30 | 45 | 60 | 60 | 70 | 80 | 90 | 100 |
(1)如果用T(h)来表示h小时后完成的工作量的百分数,请问T(5)是多少?求出T(h)的解析式,并画出图象.
(2)如果该同学在早晨8:00时开始工作,什么时候他未工作?
③ 例2、(书本P103例题4)人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为有效控制人口增长提供依据. 早在1798年,英国经济学家马尔萨斯(1766-1834)就提出了自然状态下的人口增长模型:![]() ,其中t表示经过的时间,
,其中t表示经过的时间,![]() 表示
表示![]() 时的人口数,r表示人口的年平均增长率. ……(数据和问题见P115)
时的人口数,r表示人口的年平均增长率. ……(数据和问题见P115)
(师生共析→教师小结: 指数型函数模型 →学生阅读课本,完善解题过程)
③ 例3、(书本P105例题6)、某地区不同身高的未成年男性的体重平均值研究:(数据和问题见P118)分小组讨论该选用何种函数模型来刻画这个地区未成年男性体重![]() 与身高
与身高![]() 的函数关系并分别验证,总结讨论结果,找出最恰当的函数模型,利用函数模型来解决实际问题.
的函数关系并分别验证,总结讨论结果,找出最恰当的函数模型,利用函数模型来解决实际问题.
小结:根据收集到的数据的特点,通过建立函数模型,解决实际问题的基本过程:收集数据→画散点图→选择函数模型→求函数模型→检验→符合实际,用函数模型解释实际问题;不符合实际,则重新选择函数模型,直到符合实际为止.
(三)、巩固练习:
1. 阅读P123、P73、P79 等应用问题,小结函数模型类别
2. 已知镭经过100年,质量便比原来减少4.24%,设质量为1的镭经过![]() 年后的剩留量为
年后的剩留量为![]() ,则
,则![]() 的函数解析式为 .
的函数解析式为 .
3. 某新型电子产品2002年投产,计划2004年使其成本降低36℅.则平均每年应降低成本 ℅.
4.有一批影碟(VCD)原销售价为每台800元,在甲、乙两家家电商场均有销售. 甲商场用如下方法促销:买一台单价为780元,买两台单价都为760元,依次类推,每多买一台则所买各台单价均再减少20元,但每台售价不能低于440元;乙商场一律都按原价的75%销售. 某单位需购买一批此类影碟机,问去哪家商场购买花费较低?
(四)补充例题:
★【例题】某飞机制造公司一年中最多可生产某种型号的飞机100架。已知制造x架该种飞机的产值函数为R(x)=3000x-20x2 (单位:万元),成本函数
C(x)=500x+4000 (单位:万元)。利润是收入与成本之差,又在经济学中,函数¦(x)的边际利润函数M¦x)定义为:M¦x)=¦(x+1)-¦(x).
①、求利润函数P(x)及边际利润函数MP(x);(利润=产值-成本)
②、问该公司的利润函数P(x)与边际利润函数MP(x)是否具有相等的最大值?
●解:①P(x)= R(x)- C(x)= -20x2+2500x-4000 (x∈N*,且x∈[1,100]);
MP(x)= P(x+1)- P(x)=-40x+2480(x∈N*,且x∈[1,100]);
②P(x)= -20(x-)2+74125 (x∈N*,且x∈[1,100]);则当x=62或63时,P(x)max=74120(元),因为MP(x) =-40x+2480为↘,则当x=1时,MP(x)max =2440元,故利润函数与边际利润函数不具有相等的最大值。
★【例题2】. (湖南2006年高考理科20题14分)对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为:![]() )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为![]() (1≤a≤3).设用
(1≤a≤3).设用![]() 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是![]() (
(![]() ),用
),用![]() 质量的水第二次清洗后的清洁度是
质量的水第二次清洗后的清洁度是![]() ,其中
,其中![]() 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及![]() 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当![]() 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论
为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论![]() 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
解:(Ⅰ)设方案甲与方案乙的用水量分别为x与z,由题设有![]() =0.99,解得x=19. 由
=0.99,解得x=19. 由![]() 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程: ![]() 解得y=4
解得y=4![]() ,故z=4
,故z=4![]() +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4![]() +3.因为当
+3.因为当![]() ,故方案乙的用水量较少.(II)设初次与第二次清洗的用水量分别为
,故方案乙的用水量较少.(II)设初次与第二次清洗的用水量分别为![]() 与
与![]() ,类似(I)得
,类似(I)得![]() ,
,![]() (*)于是
(*)于是![]() +
+![]()
![]() ;当
;当![]() 为定值时,
为定值时,![]() , 当且仅当
, 当且仅当![]() 时等号成立.此时
时等号成立.此时![]() 将
将![]() 代入(*)式得
代入(*)式得![]() 故
故![]() 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为 ![]() , 最少总用水量是
, 最少总用水量是![]() .
当
.
当![]() ,故T(
,故T(![]() )是增函数(也可以用二次函数的单调性判断).这说明,随着
)是增函数(也可以用二次函数的单调性判断).这说明,随着![]() 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.