高一数学函数立体几何部分测试题

___考室_______________________号 　　　　

 班级________ 班  　　　　　　　　测试内容；高一数学函数立体几何部分测试题　　　　

 姓名_______________　　　　　　　　　　  撰稿： 方锦昌　 易传庚

　　　　　 　　　　　　　　　　一、选择题（每小题5分，共50分）

1．集合{1，2}的非空真子集的个数有（　 ）

A．2个　　　　　　　　　B．3个　　　　　　　　 　　　 C．4个　　　　　　　　D．5个

2．函数的定义域是　(　 )

A. 　　　　 B. 　　　　　 C. 　　　 D.

3．如果函数在区间(-1,0)内存在零点,则a的取值可以是 (　 )

(A)　　　　　　 (B)0　　　　　　　  (C) 　　　　　　　　 (D) –1

4　已知，则的大小关系是（　　）

A　　　　 B　　　　　　C　　　　　　　 D　

5．在半径为30米的圆形广场上空，设置一个照明光源，射向地面的光呈圆锥形，其轴截面顶角为120度，若要光源恰好照亮整个广场，则光源的高度应为（　 ）米

A 10　　　　　 B　20　　　　　C　10　　　 D　20

6．若≥，则（　　）

 A．≥0　　　　　　　　B．≥0　　　　　　 C．≤0  　 D．≤0

7．若，且，则函数：（　　）

A． 且为奇函数　　　　　 　　B．且为偶函数

C．为增函数且为奇函数　　　　　  　　D．为增函数且为偶函数

8．对于平面和共面的直线、下列命题中真命题是　 （　 ）

　　（A）若则　　　　（B）若则

　　（C）若则　　　（D）若、与所成的角相等，则

9、设函数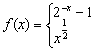 ，若，则的取值范围是　（　 ）

（A）（，1）　　　　　　　　　　　　  （B）（，）　

（C）（，）（0，）　　　　 （D）（，）（1，）

10．拟定从甲地到乙地通话m分钟的电话费由f(m)＝1.06·(0.50×[m]＋1)给出，其中m　　　　　　　　　　 ＞0，[m]是大于或等于m的最小整数（如[3]＝3，[3.7]＝4， [3.1]＝4），则从甲　　　　　　　　　　  地到乙地通话时间为5.5分钟的话费为　（　　）

　　　 A．3.71　　　　 B．3.97　　　　　　　　　　 C．4.24　　 　　　　　 　　D．4.77

二、填空题（每题5分，共25分）

11．设集合A＝｛5，｝，集合B＝｛,｝．若AB＝｛2｝，则AB＝　　　　　　　．

12、圆是以为半径的球的小圆，若圆的面积和球的表面积的比为，则圆心到球心的距离与球半径的比＿＿＿＿＿。

13．函数是幂函数，且在上是减函数，则实数__　 

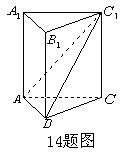14、如图，在正三棱柱中，．若二面角的大小为，则点到平面的距离为______________．

15、已知函数是R上的奇函数,则函数的图象关于_______对称; 若有2007个零点(记为),则____.

题次	1	2	3	4	5	6	7	8	9	10
答案

（一）、选择题答案：

（二）、填空题答案：　　　 11题．__________________;　　　 12题 :_____________;　　　　 13题:__________________;　14题:__________________;　　　　15题:________；________

三、解答题

16．（10分）“菊花”烟花是最壮观的烟花之一，制造时一般是期望在它达到最高点时爆裂，如果烟花距地面高度h 米与时间t 秒之间的关系为，那么烟花冲出后什么时候是它爆裂的最佳时刻？这时距地面的高度是多少（精确到1米）？

17．（12分）已知ABCD为矩形，E为半圆CED上一点，且平面ABCD⊥平面CDE．

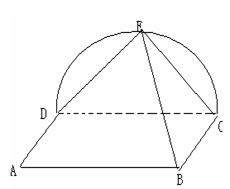（1）求证：DE是AD与BE的公垂线（6分）；

（2）若AD＝DE＝AB，求AD和BE所成的角的大小（6分）．

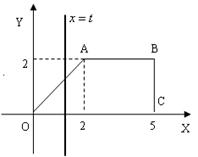
18．（12分）如图，直角梯形OABC位于直线右侧的图形面积为。（1）试求函数的解析式（8分）；

（2）画出函数的图象（4分）。

19．(本题满分12分)：已知函数f(x)=2^x - ；

(1)、求证:函数f(x)在(-1,+∞)上为增函数；（6分）

(2)、求证：函数f(x)在（0，1）内必有零点。（6分）

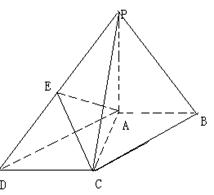20．（15分）如图，在底面为平行四边形的四棱锥中，，平面，且，点是的中点.

（Ⅰ）求证：；（5分）

（Ⅱ）求证：平面；（5分）

（Ⅲ）求二面角的大小.（5分）

21（14分）、猎豹汽车制造厂有一条价值为a万元的汽车生产线,现在要通过技术改造来提高该生产线的生产能力，提高产品的增加值。经市场调查，产品的增加值y万元与技术改造投入x万元之间满足：（1)、y与（a-x）和x的乘积成正比；（2）、当x= 时，y=a²。

又技术改造投入比率为：∈(0,t]，其中t是常数，且t∈(0,2]。

（1）、设y=f(x)，求函数y=f(x)的表达式（5分）以及定义域（3分）；

（2）、求出产品的增加值y的最大值及相应的x之值（6分）。

参考答案

题次	1	2	3	4	5	6	7	8	9	10
答案	A	B	D	C	A	B	A	C	D	C

　　　 11题．{5，1，2}　　 12题 :1：3;　　13题:　 2;　　 14题: 　　15题；原点、0

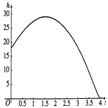16．（10分）解：作出函数的图象，显然，函数图象的顶点就是烟花上升的最高点，顶点的横坐标就是烟花爆裂的最佳时刻，纵坐标就是这时距地面的高度。由二次函数的知识，对于函数，我们有：当时，函数有最大值

于是，烟花冲出后1.5s是爆裂的最佳时刻，这时距地面的高度约为29m

17．6分+6分：60°

18．（8分+4分）

 解：（1）设直线与梯形的交点为D，E。当时 ；当时，

所以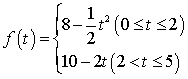 （2）图象（略）

20、（5分+5分+5分）

解：（1）由平面可得PA^AC

又，所以AC^平面PAB，所以

（2）如图，连BD交AC于点O，连EO，则

EO是△PDB的中位线，\EOPB

\PB平面

（3）如图，取AD的中点F，连EF，FO，则EF是△PAD的中位线，\EFPA又平面，\EF^平面

同理FO是△ADC的中位线，\FOAB\FO^AC由三垂线定理可知\ÐEOF是二面角E－AC－D的平面角.又FO＝AB＝PA＝EF\ÐEOF＝45°而二面角与二面角E－AC－D互补，故所求二面角的大小为135°.

21、5分+3分+6分：

解：（1）、y=f(x)=4(a-x)·x，（5分）；定义域：0<x≤；（3分）

（2）：1）、当t∈(0,]时，y_max=f()=,2)当t∈[,2]，时，y_max=f()=a²。（6分）