高一数学四月段考题
2008-4-14一．选择题 （每小题５分，共50分）
1. 
2. 若f(cosx)=cos2x-3cosx,则f(siny)的值域为
3. 下列函数中，周期为1的奇函数是
4. 
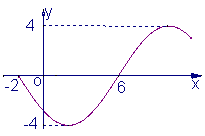函数y=Asin(wx+j)(w>0，
，xÎR)的部分图象如图所示，则函数表达式为
A.
B.
C.
D.
5. 锐角三角形的内角A、B 满足tan A - 
= tan B,则有
A. sin 2A –cos B = 0 B. sin 2A + cos B = 0
C. sin 2A – sin B = 0 D. sin 2A+ sin B = 0
6. 若非零向量
满足
，则
Ａ.
Ｂ.
Ｃ.
Ｄ. 
7. 已知向量
，若
的大小为
A. 
B.
C.
D. 
8. 设锐角
使关于x的方程
有重根，则的弧度数为
A. 
B.
C.
D.
9. 已知sinx－siny= －
，cosx－cosy= ，且x，y为锐角，则tan(x－y)的值是
A.
B.－ C.± D.
10. 若
，
,
，则
的值等于
A.
B.
C.
D.
第Ⅱ卷（非选择题 共5道填空题6道解答题）
请将你认为正确的答案代号填在下表中
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二.简答题 （每小题5分，共25分）
11. 
＝___________
12. 已知
的值为
，
的值为
.
13. 
14. 
15. 方程
在区间
内的解是_________.
三.解答题 （共75分）
16. 
17. 已知
的值.
18. 点P（2sinθ，2cosθ）在直线y= -2x上.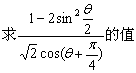
19. 已知
，
.求
和
的值.
20. 已知
，
，求sina及
21. 设a为常数f (x)
= 
, 如果对任意x∈R，不等式f (x)+ 4 ≥0恒成立，求实数a的取值范围.
2008年武昌区高一四月段考题
参考答案（仅供参考）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | A | D | A | A | C | D | B | B | B |
8. 因方程有重根，故
得
，于是
。 故选B。
10. 由
，则
，
，又
，
，所以
，
解得
，所以 ＝，故选B
二.简答题答案:
11. 本题考查三角公式的记忆及熟练运用三角公式计算求值
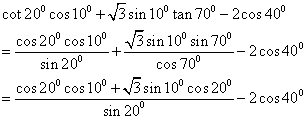
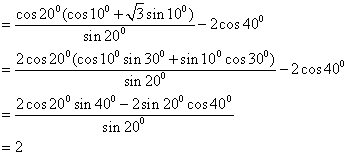
【解后反思】方法不拘泥,要注意灵活运用,在求三角的问题中,要注意这样的口决“三看”即(1)看角,把角尽量向特殊角或可计算角转化，(2)看名称,把一道等式尽量化成同一名称或相近的名称，例如把所有的切都转化为相应的弦，或把所有的弦转化为相应的切，(3)看式子,看式子是否满足三角函数的公式.如果满足直接使用,如果不满足转化一下角或转换一下名称,就可以使用.
12. 
（I）因为
所以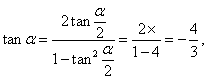
所以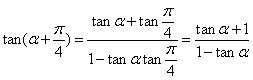
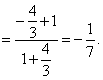
【名师指津】本题还考查了倍角的正切公式与两角和的正公式.三角函数知识的考查每年题目难度都不是很大,应该抓基本公式与基本题型的解决.
13. 
14. 增区间[kπ+
；kπ+
]（k∈Z）
15. 
三.解答题答案:
16. 
17. 解法一：由已知得：
由已知条件可知
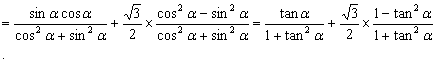
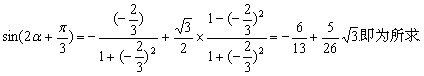
解法二：由已知条件可知
18. 由已知得 2cos =-6sinθ,（3分）即cosθ=-3sinθ，①
.
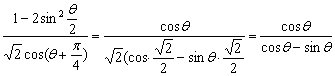
19. 本小题考查同角三角函数关系、两角和公式、倍角公式等基础知识，考查基本运算能力。
解法一：由
得
则
因为
所以
解法二：由得 
解得
或
由已知故舍去
得 
因此，
那么 
且
故
20. 解法一：由题设条件，应用两角差的正弦公式得
，即
①
由题设条件，应用二倍角余弦公式得
故
②
由①和②式得
，
因此，
，由两角和的正切公式
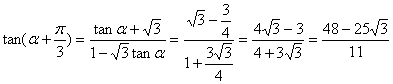
解法二：由题设条件，应用二倍角余弦公式得
，
解得 
，即
由可得
由于
，且
，故a在第二象限于是，
从而
以下同解法一
21. f (x)+ 4≥0
cos2x － (a2－3a)cosx－3≤0
设t = cosx则－1≤t≤1
g (t) = t2－(a2－3a)t－3≤0 对－1≤t≤1所有t都成立. … (4分)
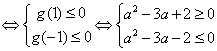…………………………………………(8分)
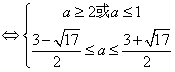………………………………………………（10分）
或
……………………………………（12分）
解法二：
同解法一得：g (t) = t2－(a2－3a) t－3≤0对－1≤t≤1的所有t均成立……（4分）
则当
≥0即a≥3或a≤0时，g (－1)≤0
a2－3a－2≤0 , 
≤a≤
3≤a≤或≤a≤0 ………………………………（7分）
当<0即0 < a < 3时，g (1)≤0
a2－3a + 2≥0 ，a≥2或 a≤1 0 < a≤1或2≤a < 3 …………………（10分）
综合得≤a≤1或2≤a≤ ………………………………… （14分）