高一数学复习竞赛试卷
学校 班级 姓名 分数
| 竞赛须知 | 1. 本试卷为闭卷考试，满分为100分，考试时间为90分钟． 2. 本试卷共7页，各题答案均答在本题规定的位置． |
一、选择题：本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后括号内．
(1) 已知函数
，
，那么集合
中元素的个数为（ ）
（A）1 （B）0
（C）1或0
（D）1或2 (2) 设
是第二象限的角，且
，则
角属于（ ）
（A）第一象限 （B）第二象限
（C）第三象限 （D）第四象限
(3) 在△ABC中，D、E、F分别BC、CA、AB的中点，点M是△ABC的重心，则
等于 （ ）
（A）
（B）
（C）
（D）
(4) 某种商品进货单价为40元，若按每个50元的价格出售，能卖出50个；若销售单价每上涨1元，则销售量就减少1个。为了获得最大利润，此商品的最佳销售单价应为（ ）
（A）70元 （B） 65元 （C） 60元 （D） 50元
(5)在
中，已知
是
边上一点，若
，
，则
（
）
（A）
（B）
（C）
（D）
(6) 设
，用二分法求方程
内近似解的过程中得
则方程的根落在区间（ ）
（A）
（B）
（C）
（D）不能确定
(7) 下面有四个命题：
①终边在y轴上的角的集合是{
}；
②在同一坐标系中，函数y=sinx和函数y=x的图象有三个公共点；
③把
的图象向右平移
得到
的图象；
④函数
在
上是减函数．
其中真命题的个数是（ ）
（A）1 （B）2 （C）3 （D）4
(8) 函数是
上的奇函数，满足
，当
∈
时
，则当∈（
，
）时，
=（ ）
（A）
（B） 
（C）
（D） 
(9) 二次函数满足
，又
，
，若在[0，
]上有最大值3，最小值1，则的取值范围是（ ）
（A） 
（B）
（C）
（D）
(10) 关于的方程
，给出下列四个命题：
①存在实数
，使得方程恰有2个不同的实根；
②存在实数，使得方程恰有4个不同的实根；
③存在实数，使得方程恰有5个不同的实根；
④存在实数，使得方程恰有8个不同的实根；
其中假命题的个数是（ ）
（A）0 （B）1 （C）2 （D）3
二、填空题：本大题共6个小题，每小题4分，共24分．把答案填在题中横线上．
(11) 设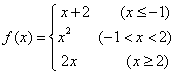
，若
，则
_______．
(12) 使方程
有解，则m的取值范围是________．
(13) 如图，在中，点
是
的中点，过点的直线分别交直线，
于不同的两点
，若
，
，则
的值为 ．
(14) 设函数
为奇函数，则实数
的值为________.
(15) 直角坐标系中横坐标、纵坐标均为整数的点称为格点，如果函数f(x)的图象恰好通过k(k∈N*)个格点，则称函数f(x)为k阶格点函数.下列函数：①f(x)＝sinx；②f(x)=π(x－1)2＋3；③f(x)＝()x；④f(x)＝log0.6x，其中是一阶格点函数的有_______________.
(16) 如图，一个半径为10米的水轮按逆时针方向每分钟转4圈．记水轮上的点P到水面的距离为d米（P在水面下则d为负数），则d（米）与时间t（秒）之间满足关系式： 
，
，且当P点从水面上浮现时开始计算时间．有以下四个结论：①
，②
，③
，④
，则其中所有正确结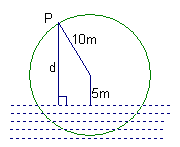
论的序号是
.
三、解答题：本大题共4个小题，共36分．解答题应写出文字说明，证明过程或演算步骤．
(17) (本小题满分8分)
1．计算：
2．已知
，分别求下列各式的值：
（Ⅰ）
；
（Ⅱ）
.
(18) (本小题满分7分)
一种放射性物质最初的质量是a克，按每年25%衰减.
（Ⅰ）求t年后，这种放射性物质的质量
的表达式；
（Ⅱ）估计约经过多少年（结果保留1个有效数字），该物质的剩留量是最初质量的
． （参考数据：
，
）
(19) (本小题满分10分)
已知函数
,( 
,为常数) ．
（Ⅰ）当
时，求
的定义域；
（Ⅱ） 当
时，判断函数
在区间
上的单调性，并写出理由；
（Ⅲ）当时，若在
上恒正，求的取值范围．
(20) (本小题满分11分)
设f(x)是定义在
的奇函数，g(x)的图象与f(x)的图象关于直线x=1对称，而当
时，
．
（Ⅰ）求f(x)的解析式；
（Ⅱ）对任意
求证：
；
（Ⅲ）对任意
求证：
．
高一数学竞赛
参考答案与评分标准
一、选择题
（共10个小题，每小题4分，共40分）
1． C 2．C 3．C 4．A 5．D
6． B 7．A 8．B 9．D 10．A
二、填空题
（共6个小题，每小题4分，共24分）
11．
12．[
13．2
14．
15．①②④ 16．①②④
三、解答题
（共4个小题，满分36分）
（17）(本小题满分8分)
1． 
2．解：（Ⅰ）由已知得 
；
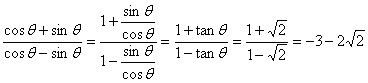（Ⅱ） 
.
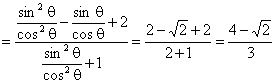(18) (本小题满分7分)
解：（Ⅰ）
；
（Ⅱ）设经过年，该物质的剩留量是最初质量的．
依题意得 
，
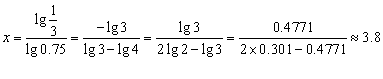
∴ 估计约经过4年，该物质的剩留量是原来的.
（19）(本小题满分10分)
略解：
（Ⅰ）的定义域为(0,+∞)；
（Ⅱ）在上是增函数；
（Ⅲ）由（Ⅱ）得 时，在上是增函数，故 在上是增函数．
当时，
对
恒成立等价于
．
(20) (本小题满分11分)
解：（Ⅰ）由题意知f(x+1)=g(1-x)
当
当
，由于f(x)是奇函数
（Ⅱ）当
（Ⅲ）当
