高一数学复习试题
1.集合Ｍ＝｛ｘ∈N*ｘ－３＜２｝的另一种表示方法是（ ）
Ａ．｛０，１，２，３，４｝ Ｂ．｛１，２，３，４｝
Ｃ．｛０，１，２，３，４，５｝ Ｄ．｛１，２，３，４，５｝
2. 下列函数中，在区间
是减函数的是（ ）
A. 
B. 
C. 
D. 
3.方程
表示的直线可能是（ ）
 |  | ||
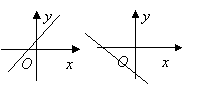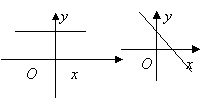A. B. C. D.
4、若两直线
与
平行，则a的值为（ ）
A、
B、2 C、和2 D、0和1
5.若函数y=f(x)在区间（-2，2）上的图像是连续不断的曲线且在（-2，2）上有且仅有一个零点，则f(-1)f(1)的值
A.大于0 B.小于0 C.等于0 D. 无法判断
6、已知ｙ＝ｆ（ｘ）是奇函数，当０≤ｘ≤４时，ｆ（ｘ）＝ｘ２－２ｘ
则当－４≤ｘ≤０时，ｆ（ｘ）的解析式是（ ）
Ａ、ｘ２－２ｘ Ｂ、－ｘ２－２ｘ Ｃ、－ｘ２＋２ｘ Ｄ、ｘ２＋２ｘ
7.若圆柱的底面半径及高都等于一个球的直径,圆柱的体积是
,则球的体积是( )
8.在空间直角坐标系中
位于
A.
轴上 B.
轴上 C.
平面内 D.
平面内
9、已知圆C：（x-a）2+(y-2)2=4(a>0)及直线L:x-y+3=0.当直线L被C截得的弦长为2
时
则a= （ ）
A 。
B。
C。-1
D。+1
| |
的单调递增区间是（ ）
| |
B. 
C. 
D. 
11.春天来了，某池塘中的荷花生长旺盛，已知每一天荷叶覆盖水面面积是前一天的2倍， 20天完全长满池塘水面，
当荷叶刚好覆盖水面面积一半时，荷叶已生长了
A 10天 B 15天 C 19天 D 20天
12方程
的根在区间（ ）上
A。（0，1） B。（1，2） C。（2，3） D。（3，4）
13计算
=
14.原点O在直线L上的射影为点H(-2,1)，则直线L的方程为___________.
15. 设函数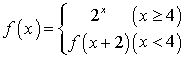
，则
=
16. m、n表示直线，α、β、γ表示平面，给出下列四命题
①α
β=m,n
α,n⊥m,则α⊥β
②α⊥β，αγ=m, βγ=n,则m⊥n
③α⊥β, α⊥γ, βγ=m,则m⊥α
④m⊥α，n⊥β, m⊥n, 则
其中正确命题为_______________.
17.已知直线
和直线
平行，与两坐标轴围成的三角形的面积是6，求直线的方程；
18. 如图示：四边形ABCD是边长为6的正方形，AE⊥平面CDE，且AE=3，Ｍ、Ｎ分别为BE、ED的中点
|
（2）求证：平面ABCD⊥平面ADE .
19．设圆上的点A(1,4)关于直线x-y+1=0的对称点仍在圆上，且与直线x+y-2=0相交的弦长为
，求圆的方程。
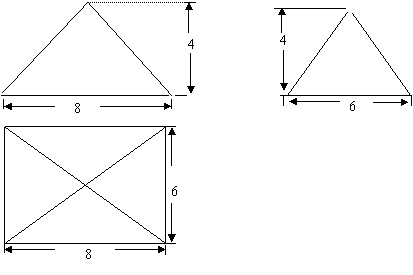20已知某几何体的俯视图是如图所示的矩形，主视图是一个底边长为8，高为4的等腰三角形，左试图是一个底边长为6，高为4的等腰三角形。
（1）求该几何体的体积；
（2）求该几何体的侧面积。
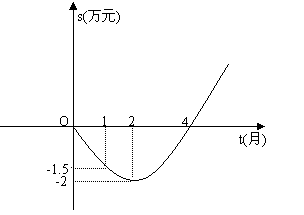21. 2007年，某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程。下面的二次函数图像（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s与t之间的关系）。根据图像提供的信息解答下列问题：
（1） 由已知图像，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2） 求截止到几月末公司累积利润可达到30万元；
（3） 求第八个月公司所获利润是多少万元？
22.已知函数f(x)=
.
（1） 求f(x)的定义域；
（2） 判断并证明f(x)的奇偶性；
（3）在（0，1）内，求使关系式f(x)>f(
)成立的实数x的取值范围。
参考答案
BDABD BCCCB CC
2 y=2x+5 48 ③④
17.解：设方程为x-3y+m=0，与坐标轴的交点坐标（0，
）,(-m,0),..................................4分
由面积为6， 则-m=12,解的m=
........................8分
根据题意m=6去掉.......................10分
所以的方程为x-3y-6=0.......................12分
18.解： 解：（1）连接BD，因为Ｍ、Ｎ分别为BE、ED的中点
所以ＭＮ∥ＢＤ，又ＢＤ平面ＡＢＣＤ，ＭＮ
平面ＡＢＣＤ
∴ＭＮ∥平面ABCD........................4分
（２）∵
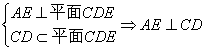........................7分
又四边形ABCD是正方形
∴ＣＤ⊥ＡＤ
又∵ＡＤ∩ＡＥ＝Ａ
∴ＣＤ⊥平面ＡＤＥ.......................10分
又ＣＤ平面ABCD
∴平面ABCD⊥平面ＡＤＥ........................12分
19。解：法Ⅰ：设圆的方程为
由已知可得：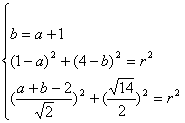
........................6分
........................10分
所以圆的方程为
......................12分
法Ⅱ：设圆的方程为
由已知可得：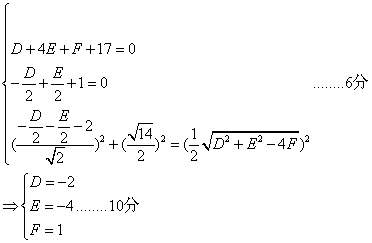
∴圆的方程为
.......................12分
２0。由三视图可知此几何体为四棱锥，底面为矩形，长8宽6的，高为4。
（1）V=
=64........................6分
(2)侧面为四个等腰三角形，左右两个的高为
，前后两个的高为5，
S=
.......................12分
21. 解：（1）由二次函数的图像可知，设二次函数的关系式为 s=at2+bt+c,
代入点的坐标 得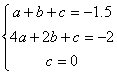
.....................3分
解得a=
, b=-2, c=0∴s=t2-2t. ....................6分
(2) 把s=30代入，得t1=10,t2=-6(舍)，∴截止到10月末公司累积利润可达到30万元。....................9分
（3）把t=7代入，得s=10.5, 把t=8代入，得s=16, 16-10.5=5.5
∴第八个月公司获利润5.5万元。.....................12分
22.解：（1）函数f(x)有意义，需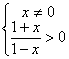
解的-1<x<1,且x≠0,∴定义域为{x-1<x<0,或0<x<1}........................4分
(2)函数f(x)为奇函数。∵f(-x)=
∴为奇函数。.......................8分
（3）设0<x1<x2<1, ∵
又0<x1<x2<1, ∴
（1）
又
，又0<x1<x2<1, ∴
∴
（2）
由（1）（2）得f(x1)-f(x2)>0∴f(x)在（0，1）内是递减的。又因为f(x)>f(),所以0<x<为所求。........................14分