_________班 姓名_______
学号：_____号 高一修一和必修二期末综合测试(3)
撰稿： 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一、 选择题（每小题5分，共10小题，共50分）
1、已知a=
，集合A={xx
3},则下列关系式正确的是：
A、aÏA； B、aÍA ； C、a∈A D、{a}∈A
2、下列式子的运算结果不是负数的是：
A、
B、
C、
D、
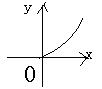
3、已知f(x)=
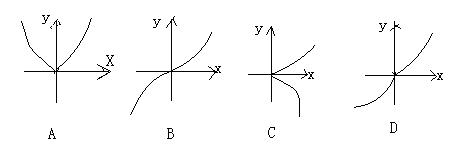
（x>0）的部分图象如图所示，则它的全部图象大致是：
4、根据下表：
| x | 4 | 5 | 6 | 7 | 8 |
| ¦(x) | 15 | 18 | 21 | 24 | 27 |
则可判断函数f(x)最有可能的函数模型是：
A、指数函数 B、一次函数 C、对数函数 D、幂函数
5、在空间，垂直于同一直线的两条直线的位置关系是：
A、平行 B、异面 C、相交 D、不能确定
6、已知直线L：ax+by+c=0满足：ab<0且bc<0，则它必定经过的象限是：
A、一、二、三 ； B、一、二、四； C、一、三、四； D、二、三、四，
7、设圆x2
+y 2 - 4x =0交直线3x+4y+2=0于点A、B，则线段AB的垂直平分线方程是：
A、4x-3y-8=0; B、4x-3y-2=0;
C、3x+4y+6=0; D、3x+4y+8=0
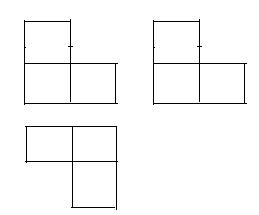
8、由大小相同的正方体木块堆成的几何体的三视图如图所示，则此几何体共有木块多少块：
A、4； B 、5； C、 6； D、7
9、关于函数f(x)=
,有以下的命题：（1）其图象关于y轴对称；（2）、它在（-∞，0）上是减函数；（3）、它有最小值为
；（4）、它在（1，+∞）是是增函数，其中正确的命题是：
A、（1）、（2） B、（2）（3）；
C、（2）（4）； D、（1）（3）（4）
10、由函数y=
和函数y=
的图象和直线y=-2,以及直线y=3所围成的封闭图形的面积是：
A、5 B、10 C、15 D、20
二、填空题(每题5分,共25分)：
11、已知经过点A(-m,6)、B(2,3m)的直线L的倾斜角为45°度，则m的值是____
12、把表面积分别为36
、64、100的三个锡球熔成一个大的锡球，则此大锡球的体积是_____
13、已知圆C：x2 +y 2 - 4x +F=0，它交y轴于点A、B两点，且∠ACB=90°，则F等于_____
14、已知集合A={直线}，B={平面}；C=A∪B，且a∈A，b∈B，c∈C；则在下列
命题（1）、
∥c；命题（2）、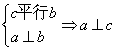
；命题（3）、
；
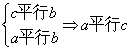命题（4）、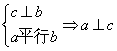
；在这些命题中，所有正确的命题的序号是______
15、已知函数
，则f(16)的值为____
一、选择题答案：
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题答案： 11题、_____________ ; 12题：_____________
13题:_____________ 14题: ______________ 15题：_________
三、解答题：
16(10分)、设集合A={-3，
，1+a },B={a-3, 
,2a-1},若AB={-3}，求出a的值。
17(13分)、首都钢铁厂生产的某种零件，成本价为40元/个，出厂价为60元/个，为鼓励销售商订购，首都钢铁厂采取以下优惠政策：凡一次性购量超过100个时，每多购一个，所购的全部零件按出厂价每个降低0.02元计算总价,但实际出厂价不能低于51元/个.请问:
(1)、当一次性购多少个零件时，实际的出厂价恰好为51元/个？
（2）、设一次性订购零件x个，所购零件的实际出厂价为y元，写出函数y=f(x)的表达式；
（3）、当销售商一次性购买零件个数为500个时，首都钢铁厂所获得的利润是多少元？
18(13分)、如图，已知PA⊥矩形ABCD所在的平面，M、N分别是AB、PC之中点，
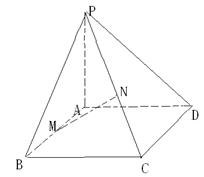（1）、求证：MN∥平面PAD
（2）、求证：MN⊥CD
（3）、设PA=a,AB=b,AD=c,求PC的长。
19(13分)、已知直线L：y=kx+3与圆O：x2 +y 2 =16，
（1）、试判断直线L与圆O的位置关系？
（2）、当k为何值时，圆心O到直线L的距离为2？
（3）、当k为何值时，直线L被圆O所截得的弦长最小，其最小的弦长是多少？
20(13分)、设函数f(x)=
满足f(1)=1，f(2)=
（1）、求出b、c之值，（2）证明：函数f(x)在[-1，1]上为减函数。
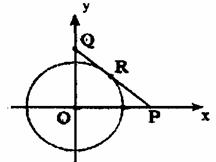
21．(13分)设有半径为3
的圆形村落，现有甲、乙两人同时从村落中心出发，甲向北直行，乙先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线方向前进，后来恰与甲相遇.设甲、乙两人速度一定，其速度之比为3：1，问甲、乙两人在何处相遇？
参考答案：
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | B | B | D | A | A | A | D | B |
11题．4 ; 12题：288 13题:-4 14题:（2）
15题：1
16题：a=-1,注意a=0要舍去
17、（1）、一次性订购x= 
+100=550；
（2）、
（3）、当订购500个时，利润为6000元。
18、（3）
19、（1）相交；（2）、k= 
；（3）当k=0时，L= 
20、b= -2, c= 2
20、如图建立平面直角坐标系，由题意可设甲、乙两人速度分别为3v千米/小时、v千米/小时，再设出发x0小时，乙在点P处改变方向，又经过y0小时，乙在点Q处与甲相遇.则P、Q两点坐标为（3vx0, 0）、（0,vx0+vy0）；由OP2+OQ2=PQ2知，（3vx0）2+(vx0+vy0)2=(3vy0)2,即
.
……①。将①代入
又已知PQ与圆O相切，直线PQ在y轴上的截距就是两个相遇的位置.
设直线
相切，
则有
答：甲、乙相遇点在离村中心正北千米处