高一年段数学（必修1）模块考试题
试题及答案卷
一：选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.选项填涂在答题卡上。
1、设全集U={1，2，3, 4，5, 6，7，8}，集合S={1, 3, 5}, T={3, 6}，则Cu(SUT)=( B )
A．
B、{2, 4，7, 8} C、{1,
3，5, 6} D、{2,
4，6, 8}
2、已知集合
，那么
的非空真子集的个数是（ D ）
A、15 B、16 C、3 D、14
3、下列各组函数中，表示同一函数的是（C）
A 、
B、
C 、
D、
4、已知集合
，下列不表示从P到Q的映射的是（ C ）
A、
B、
C、
D、
5、函数
的定义域为[4，7]，则
的定义域为（D）
A、（1，4） B [1，2] C、
D、 
6．若函数
在区间
上是减函数，则实数
的取值范围是（A）
A、
B、
C、
D、
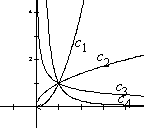7．如图的曲线是幂函数
在第一象限内的图象. 已知
分别取
，
四个值，与曲线
、
、
、
相应的依次为（A ）．
A．
B．
C．
D．
8．函数f(x)=loga
,在（－1，0）上有f(x)>0，那么 （ C ）
A．f(x)(－ 
,0)上是增函数 B．f(x)在（－，0）上是减函数
C．f(x)在（－，－1）上是增函数 D．f(x)在（－，－1）上是减函数
9．函数y=
的值域为（ A ）
A．｛yy≠1｝ B．｛yy＞1｝ C．｛yy＞2｝ D．｛y－1＜y＜2}
10．函数y=
的图象是
（ D ）
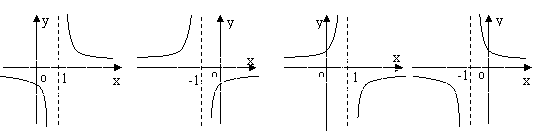
A B C D
11．若函数
的定义域为[0 ，m],值域为
，则 m的取值范围是（ C ）
A、[0 ，4] B、[
，4] C、[ ，3] D、
12．某地的中国移动“神州行”卡与中国联通130网的收费标准如下表：
| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲：联通130网 | 12元 | 每分钟0.36元 | 每6秒钟0.06元 |
| 乙：移动“神州行”卡 | 无 | 每分钟0.6元 | 每6秒钟0.07元 |
(注:本地话费以分钟为单位计费,长途话费以6秒钟为单位计费)
若某人每月拨打本地电话时间是长途电话时间的5倍,且每月通话时间(分钟)的范围在区间(60,70)内,则选择较为省钱的网络为 （ A ）
A.甲 B.乙 C.甲乙均一样 D.分情况确定
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在答题纸上。
13、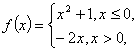
若
,则 x= -3.
.
4．设
, 用二分法求方程
内近似解的过程中, 计算得到
则方程的根落在区间 （1.25，1.5）
.
15．已知定义在R上的奇函数f(x)，当x>0时，
，那么x<0时，f(x)=
.
16．老师给出一个函数y=f（x）.四个学生甲、乙、丙、丁各指出这个函数的一个性质：
甲：对于x∈R,都有f（1+x）=f（1－x）； 乙：在（－∞, 0）上函数递减；
丙：在（0,+∞）上函数递增； 丁：f（0）不是函数的最小值.
如果其中恰有三个学生说得正确,请写出一个这样的函数： 
.
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
17.（本小题满分12分）已知M={x -2≤x≤5}, N={x a+1≤x≤2a-1}.
（Ⅰ）若M
N，求实数a的取值范围；（Ⅱ）若M
N，求实数a的取值范围.
解：（Ⅰ）由于MN，则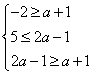
，解得a∈Φ…………………………….4
（Ⅱ）①当N=Φ时，即a＋1＞2a－1，有a＜2…………………………………….…….8
②当N≠Φ，则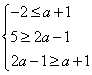
，解得2≤a≤3，.
综合①②得a的取值范围为a≤3……………………………………………………12
18、（本小题满分12分）
利用单调函数的定义证明：函数
上是减函数.
.证明：设
是区间
上的任意两个实数，且
…………… 1分
则 
……………………………………………
4分
…………………………………………………….. 6分
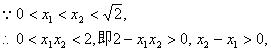
………………………………. 8分
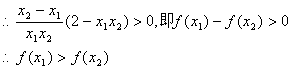
………………….10分
由单调函数的定义可知，函数上是减函数…………….12分
19．某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元．该厂为鼓励销售商定购，决定当一次定购量超过100件时，每多定购一件，定购的超过部分服装单价就降低0.02元．根据市场调查，销售商一次定购量不会超过500件．
（Ⅰ）设一次定购量为
件，服装的实际出厂单价为P元，写出函数P=f(x)的表达式；
（Ⅱ）当销售商一次定购了450件服装时，该服装厂获得的利润是多少元？（服装厂售出一件服装的利润=实际出厂价格－成本）
．解：（Ⅰ）由题意可知：
………………………5分
…………………………6分
（Ⅱ）∵x=450，
∴P=62－0.02×450=53(元)，
∴450×(53－40)=5850(元)．………………………………………………………11分
答：（Ⅰ）函数
；
（Ⅱ）当销售商一次定购了450件服装时，该服装厂获得利润为5850元．…12分
20．已知函数
.
（1）求证：不论为何实数
总是为增函数；
（2）确定的值，使为奇函数；
（3）当为奇函数时，求的值域。
解： (1) 
的定义域为R, 设
,
则
=
,
, 
,
即
,所以不论为何实数
总为增函数.
(2) 为奇函数, 
,即
,
解得: 
（3）由(2)知
, 
,
,
所以的值域为
21、已知定义在[1，4]上的函数f(x)＝x2-2bx+
(b≥1)，
(I)求f(x)的最小值g(b)；
(II)求g(b)的最大值M。
解：f(x)=(x-b)2-b2+的对称轴为直线x＝b（ b≥1），
(I) ①当1≤b≤4时，g(b)＝f(b)＝-b2+;
②当b＞4时，g(b)＝f(4)＝16-
，
综上所述，f(x)的最小值g(b)＝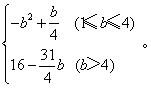
(II) ①当1≤b≤4时，g(b)＝-b2+＝-(b-
)2+
，
∴当b＝1时，M＝g(1)＝-
；
②当b＞4时，g(b)＝16-是减函数，∴g(b)＜16-
×4＝-15＜-，
综上所述，g(b)的最大值M= -。
22．（本题满分14分）
设函数
，
，且方程
有实根。
⑴证明：
且
⑵若
是方程的一个实根，判断
的正负并加以证明。
解：⑴由，知
∴
又∵
，故
，∴
.又∵有实根，即
有实根，故
，即
，∴
或
，由题设条件知得，由知
⑵∵
且
∴
∴
∴
即的符号为正。