高一年级3月考数学试题
(A卷)
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。全卷共150分。考试用时120分钟。
第Ⅰ卷（选择题 共50分）
注意事项：
1. 答卷前，考生务必将自己的姓名、考号填写在答题卷上；
2. 每小题选出答案后，把答案代号（A、B、C、D）填在答题卡上，答在试题卷上无效。
3. 交卷时只交答题卷。
一、 选择题：本大题共10小题，每小题5分，共50分。在每个小题给出的四个选项中，只有一项是符合题目要求的。
1、已知
在二象限，P
为其终边上一点，且
，则
的值是（ ）
A、 
B、
C、
D、
2、
等于 ( )
A、cos10°+sin10° B、-cos10°-sin10°
C、
D、cos10°-sin10°
3、已知
，那么cos(a+b)的值等于 ( )
A、-1 B、0 C、1 D、±1
4、已知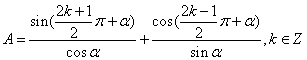
，则A的值组成的集合是 ( )
A、{1，-1，2，-2} B、{1，-1} C、{2，-2} D、{1，-1，0，2，-2}
5、若
，则
为（ ）
6、若f(sinx)＝cos18x，则f(
)＝( )
A. 
B.± C. D.±
7、
的最小值是 ( )
A、
B、
C、2 D、-2
8、已知
等于 ( )
A、2 B、3 C、4 D、5
9、△ABC中，已知sinA=
,cosB=
,则sinC的值为( )
A. 
或
B.
C.-
D.
10、设
,
,
,则
的大小是( ).
A、
B、
C、
D、
第Ⅱ卷（非选择题 共100分）
二、 填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡相
应的位置。
11、设q是第三象限角，且
，则
是第__________
象限角
12、在
ABC中，
，
，则
=____________
13、若sinα＝
,cosα＝
,则cotα的值为
.
14、已知sinθ+cosθ＝
(0＜θ＜π
，则cos2θ的值为______________.
15、已知α，β∈(0，
)，且3sinβ＝sin(2α+β)，4tan
＝1-tan2，则α+β
的值是 .
三、 解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤。
16、（本小题满分12分）
化简：
17、（本小题满分12分）
已知一扇形的圆心角是,所在圆的半径是R.
(1)若
,R=10
,求扇形的弧长及该弧所在弓形面积.
(2)若扇形的周长是一定值C,当多少弧度时,该扇形有最大面积?
18、（本小题满分12分）
设函数
满足
（1）求
的值； （2）（2）当
,求
的取值范围
19、（本小题满分12分）
已知
.
(1) 求sinx－cosx的值
(2) 求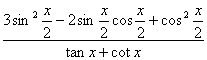
的值.
20、（本小题满分13分）
已知:
,
且
,
,求
的值.
21、（本小题满分14分）
设关于x的函数
的最小值为
．
⑴
写出的表达式；
⑵试确定能使
的
值，并求出此时函数
的最大值
08春高一3月考数学(A)参考答案
一、选择题:1---10题:ADACB,BBCAA
二、填空题:11)四;
12)
;13) 0或
;14) 
;15)
三、解答题:
16、解:原式=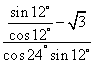
=
………………4分
=
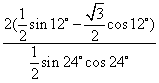……………………………10分
=
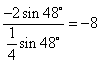………………………………12分
17、解 (1)
……………………………………2分
=
=
…6分
(2)C=2R+
=
;R=
…………………………7分
S=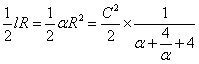
……………………9分
在(0,2
上为减函数,在[2,
上为增函数,所以:
时,
,
……………………………12分
18、(1)
………………………………….3分
(2)
……………………………7分
∵
,∴
,
∴ 
…………………………………12分
19、解法一：
（Ⅰ）由
即 
又
故 
……………………………..6分
（Ⅱ）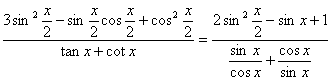
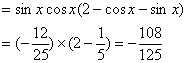………………………….12分
|
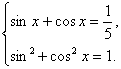
由①得
将其代入②，整理得
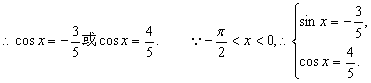
故
………………………..6分
（Ⅱ）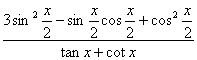
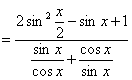
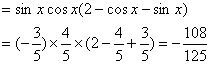………………………..12分
20、解:
……………….4分
∵, ∴
∵
∴ 
;
∵ ∴ 
∵
∴
………………………………8分
=
-
=
=
………………………………13分
21．(1)f(x)＝2(cosx－)2－－2a－1。………………………..2分
当a≥2时，则cosx＝1时，f(x)取最小值，即f(a)＝1－4a；
当－2＜a＜2时，则cosx＝时，f(x)取最小值，即f(a)＝－－2a－1；
当a≤－2时，则cosx＝－1时，f(x)取最小值，即f(a)＝1；
综合上述，有f(a)＝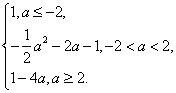
………………………8分
(2)若f(a)＝，a只能在[－2,2]内。
解方程－－2a－1＝，得a＝－1，和a＝－3。因－1∈[－2,2]，故a＝－1为所求，……………..11分
此时f(x)＝2(cosx＋)2＋；当cosx＝1时，f(x)有最大值5。……………..14分