高一年级数学上册第四次月考
满分:150分 时间:120分钟 命题人:袁明凯
要求:在答题卡上作答
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,
只有一项是符合题目要求的。)
1.全集![]() ,
,![]() ,
,![]() 则
则![]() ∩
∩![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值之差为
上的最大值与最小值之差为![]() ,则
,则![]() ( ) www.xkb123.com
( ) www.xkb123.com
A.![]() B.2
C.
B.2
C.![]() D.4
D.4
3.已知![]() 的三个内角分别是A、B、C,“
的三个内角分别是A、B、C,“![]() ”是“A、B、C的大小成等差数列”的( )
”是“A、B、C的大小成等差数列”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
4.已知集合![]() ,
,![]() ,那么
,那么
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在等差数列![]() 中,若
中,若![]() , 则
, 则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设![]()
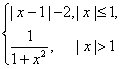 ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )
A.63 B.45 C.36 D.27
8.设![]() ,那么
,那么![]() 、
、![]() 、
、![]() 之间的大小顺序是( )
之间的大小顺序是( )
A.![]() <
<![]() <
< ![]() B.
B.![]() <
< ![]() <
<![]()
C.![]() <
<![]() <
< ![]() D.
D.![]() <
<![]() <
<![]()
9.在各项都是正数的等比数列![]() 中,若
中,若![]() ,则
,则![]()
![]()
![]()
![]() ( )
( )
A.12 B.10 C.16 D.5
10.设集合A和集合B都是自然数集合N,映射![]() 把集合A中的元素
把集合A中的元素![]() 映射到集合B中的元素
映射到集合B中的元素![]() ,则在映射
,则在映射![]() 下,象20的原象是( )
下,象20的原象是( )
A.2 B.3 C.4 D.5
11.将函数![]() 的图像向左平移1个单位得到图像
的图像向左平移1个单位得到图像![]() ,将
,将![]() 向上平移一个单位得到
向上平移一个单位得到![]() ,再作
,再作![]() 关于直线
关于直线![]() 的对称图像
的对称图像![]() ,则
,则![]() 的解析式是( )
的解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.已知实数![]() 满足等式
满足等式![]() ,下列五个关系式:
,下列五个关系式:
①![]() ②
②![]() ③
③![]() ④
④![]() ⑤
⑤![]()
其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,共20分。)
13.已知![]() 的定义域为
的定义域为![]() ,则
,则![]() 定义域为
。
定义域为
。
14.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 。
。
15.已知![]() ,函数
,函数![]() 图象与
图象与![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 。
。
16.已知函数![]() ,则
,则![]()
![]()
![]()
![]() 。
。
 高一年级第四次月考
高一年级第四次月考
数学试题答题卡 得分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
一、选择题:(本大题共12小题,每小题5分,共6 0分)
二、填空题:(本大题共4小题,每小题5分,共20分)
13. 14.
15. 16.
三、解答题(本大题共6小题,共70分,解答时应写出文字说明、证明过程或演算步骤。)
17.(本题满分10分)![]() 是什么数时,函数
是什么数时,函数![]() 的值:(1)等于
的值:(1)等于![]() ?(2)是正数?(3)是负数?
?(2)是正数?(3)是负数?
18.(本题满分12分)计算下列各式:(1)![]()
(2)![]()
19.(本题满分12分)设等比数列![]() 的公比
的公比![]() ,前
,前![]() 项和为
项和为![]() .已知
.已知![]() ,求
,求![]() 的通项公式.
的通项公式.
20.(本题满分12分)设函数![]() (
(![]() 、
、![]() ),若
),若![]() ,且对任意实数
,且对任意实数![]() ,不等式
,不等式![]()
![]() 0恒成立。
0恒成立。
(1)求实数![]() 、
、![]() 的值;
的值;
(2)当![]() [-2,2]时,
[-2,2]时,![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围。
的取值范围。
21.(本题满分12分)已知函数![]()
![]() 。
。
(1)求![]() 的定义域; (2)求使
的定义域; (2)求使![]() 的
的![]() 取值范围; (3)求
取值范围; (3)求![]()
22.(本题满分12分)已知数列![]() 满足
满足![]() ,令
,令![]() 。
。
(1)求![]() 的值;(2)求证:数列
的值;(2)求证:数列![]() 是等差数列;(3)求数列
是等差数列;(3)求数列![]() 的通项公式。
的通项公式。
参考答案
一、选择题:ADCDB BBCBA CB
二、填空题:
13、![]() 14、
14、![]()
15、![]() 16、2007
16、2007
三、解答题:
17、解:(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 。
。
18、解:(1)![]() ; (2)
; (2)![]()
19、解:由题设知![]() ,
,
则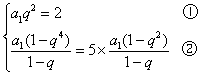
由②得![]() ,
,![]() ,
,![]() ,
,
因为![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,代入①得
时,代入①得![]() ,通项公式
,通项公式![]() ;
;
当![]() 时,代入①得
时,代入①得![]() ,通项公式
,通项公式![]() .
.
20、解:(1)∵![]() ∴
∴![]()
∵任意实数x均有![]()
![]() 0成立∴
0成立∴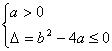
解得:![]() ,
,![]()
(2)由(1)知![]()
∴![]() 的对称轴为
的对称轴为![]()
∵当![]() [-2,2]时,
[-2,2]时,![]() 是单调函数
是单调函数
∴![]() 或
或![]()
∴实数![]() 的取值范围是
的取值范围是![]()
21、解:(1)由![]() 可知:
可知:![]()
解之得:![]()
![]() 函数的定义域为
函数的定义域为![]()
(2)由![]() 得:
得:![]()
![]() 由对数函数的单调性知
由对数函数的单调性知 ![]()
又由(1)可知![]()
![]()
![]()
![]() 由对数函数的单调性知
由对数函数的单调性知 ![]()
又由(1)可知![]()
![]()
![]()
(3)![]()
22、解:(1)![]()
(2)![]()
![]()
![]()
![]() 即
即![]()
![]() 数列
数列![]() 是等差数列
是等差数列
(3)![]() 数列
数列![]() 是等差数列
是等差数列 ![]()
![]() 即
即![]()
![]()