第一学期第一学段模块考试
高一年级数学必修2试卷
命题人:贾双喜 审题人:潘伟军 2008-1-19
[说明] 本试卷分为Ⅰ、Ⅱ卷两部分,满分100分,考试时间100分钟。第Ⅰ卷为试题卷,第Ⅱ卷为答题卷。请将各题的答案写在第Ⅱ卷相应的位置上。
(第Ⅰ卷)
一、选择题:(本大题共16小题,每小题3分,共48分,请将正确答案的代号写在第Ⅱ卷相应的空格内)
1、直线x-![]() y-
y-![]() =0的倾斜角是…………………………………………( A )
=0的倾斜角是…………………………………………( A )
| A. 300 | B. 600 | C. 1200 | D. 1500 |
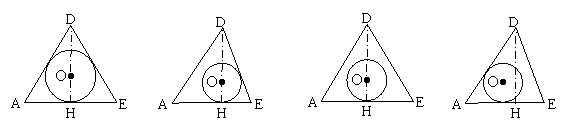
2、已知正四面体ABCD及其内切球O,经过该四面体的棱AD及底面ABC上的高DH作截面,交BC于点E,,则截面图形正确的是…………………( B )
|
| B. | C. | D. |
3、经过点P(-1,3)且与直线x-2y+3=0垂直的直线方程是………………( B )
| A. 2x+y+1=0 | B. 2x+y-1=0 | C. x-2y+7=0 | D. x-2y-7=0 |
4、在下列三个判断:
①两条相交的直线确定一个平面;
②两条平行的直线确定一个平面;
③一点和一条直线确定一个平面
中,正确的个数是……………………………………………………………( C )
| A. 0 | B. 1 | C. 2 | D. 3 |
5、若直线2x-3y+3=0与直线6x+ay-3=0平行,则a=……………………( C )
| A. -4 | B. 4 | C. -9 | D. 9 |
6、由原点向圆C:x2+y2+4x-2y+2=0引切线,则切线的长为……………( A )
| A. | B. | C. | D. 2 |
7、轴截面是正三角形的圆锥的表面积与它的外接球的表面积的比是……( D )
| A. 1∶2 | B. 1∶3 | C. 3∶8 | D. 9∶16 |
8、若三棱锥P-ABC的三条侧棱与底面所成的角都相等,则点P在底面ABC上的射影一定是DABC的………………………………………………………( A )
| A. 外心 | B. 垂心 | C. 内心 | D. 重心 |
9、一束光线自点A(3,2,1)发出被xOy平面反射,到达点B(-3,0,2)被吸收,那么光线自点A至点B所走的距离是………………………………………( D )
| A. 3 | B. | C. | D. 7 |
10、在下列命题
①过空间一点作已知直线的垂线有且只有一条;
②过空间一点作已知平面的垂线有且只有一条;
③过空间一点作已知直线的垂面有且只有一个;
④过空间一点作已知平面的垂面有且只有一个
中,正确命题的个数是………………………………………………………( B )
| A. 1 | B. 2 | C. 3 | D. 4 |
11、两圆x2+y2=2和x2+y2+2y=0的公共弦所在直线的方程为……………( D )
| A.x=1 | B.x=-1 | C. y=1 | D. y=-1 |
12、两直线3x-2y+6=0和2x-3y-6=0的交点在……………………………( C )
| A. 第一象限 | B. 第二象限 | C. 第三象限 | D. 第四象限 |
13、已知a、b是两条不同的直线,a、b是两个不同的平面,在下列命题
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
中,正确命题的个数是………………………………………………………( B )
| A. 1 | B. 2 | C. 3 | D. 4 |
14、如图,已知正方形ABCD的边长为2,沿对角线AC将三角形ADC折起,使平面ADC与平面ABC垂直,折叠后B、D两点的距离是……………( B )
| A.1 | B.2 | C. | D. |
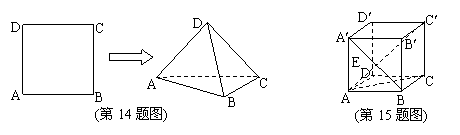
15、如图,在正方体ABCD-A¢B¢C¢D¢中,直线A¢B和直线AC、CC¢、C¢A所成的角的大小分别是a、b、g,则a、b、g的大小分别是……………………( A )
| A. b<a<g | B. a<b<g | C. a<g<b | D. b<g<a |
16、直线l:ax+by=0和圆C:x2+y2+ax+by=0在同一坐标系的图形只能是…( D )
|
| B. | C. | D. |
二、填空题:(本大题共4小题,每小题3分,共12分,请将正确答案写在第Ⅱ卷相应的横线上)
17、两平行直线4x-3y+3=0和4x-3y-7=0之间的距离为__ 2 _____;
18、以点C(-1,2)为圆心且与x轴相切的圆的方程为(x+1)2+(y-2)2=4;
19、已知三棱柱ABC-A´B´C´所有的棱长均为2,且侧棱与底面垂直,则该三棱柱的体积是 ![]() (立方单位);
(立方单位);
20、已知直线a、b及平面a,在下列命题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
中,正确的有 ① ③ (只填序号).
三、解答题:(本大题共4小题,每小题10分,共40分)
21、已知A(1,0)、B(0,1)、C(-3,-2)三点.
(1)试判断三角形ABC的形状;
(2)求三角形ABC的面积.
解:(1)kAB=-1,kBC=1,(2¢)kAB×kBC=-1,∴AB^BC,(4¢)
∴三角形ABC是直角三角形. (5¢)
(2)![]() ,
,![]() (8¢)
(8¢)
∴三角形ABC的面积为
![]() (平方单位). (10¢)
(平方单位). (10¢)
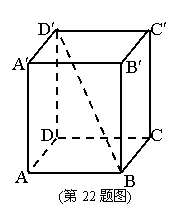 22、如图,在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为450,求:
22、如图,在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为450,求:
(1)长方体AC¢的高;
(2)长方体AC¢的表面积;
(3)几何体C¢D¢-ABCD的体积.
解:(1)连结BD,∵DD¢^平面ABCD,
∴Ð DBD¢是直线BD¢与平面ABCD所成的角.
∴Ð DBD¢=450,(2¢)∴DD¢= BD,
又AB=3,BC=4,∴DD¢= BD=5,
∴长方体AC¢的高为5.(4¢)
(2)长方体AC¢的表面积S=2(3´4+4´5+5´3)=94(平方单位)(7¢)
(3)几何体C¢D¢-ABCD的体积V=![]() (3´4´5)=30(立方单位). (10¢)
(3´4´5)=30(立方单位). (10¢)
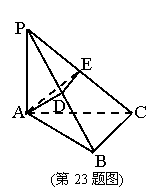 23、如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
23、如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
(1)当DE//BC时,求证:直线PB^平面ADE;
(2)当DE^PC时,求证:直线PC^平面ADE;
(3)当AB=BC时,求二面角A-PC-B的大小.
(1)证:∵AP=AB,点D是PB的中点,∴AD^PB,
∵AP^平面ABC,BCÌ平面ABC,
∴AP^BC,∵AB^BC,∴BC^平面PAB,
∵PBÌ平面PAB,∴BC^PB,
∵DE//BC,∴DE^PB,∴PB^平面ADE. (3¢)
(2)证:∵BC^平面PAB,ADÌ平面PAB,∴BC^AD,
又AD^PB,∴AD^平面PBC,∵PCÌ平面PBC,
∴AD^PC,
又DE^PC,∴PC^平面ADE. (6¢)
(3)由(2)可知,当DE^PC时,PC^平面ADE,
∴ÐAED是二面角A-PC-B的平面角. (7¢)
设AP=a,则AB=BC=a,![]() ,
,![]() ,(8¢)
,(8¢)
∵AD^平面PBC,DEÌ平面PBC,∴AD^DE,
在RtDADE中,可求得,![]() ,
,![]() ,(9¢)
,(9¢)
∴![]() ,∴ÐAED=600,
,∴ÐAED=600,
∴二面角A-PC-B的大小为600. (10¢)
24、已知直线l :kx-y+1=0,圆C:x2+y2-4x-5=0,
(1)求证:无论k取任何实数,直线l与圆C恒有两个不同的交点;
(2)当k=2时,直线l与圆C相交于A、B,求A、B两点间的距离;
(3)当实数k变化时,求直线l被圆C截得的弦的中点的轨迹方程.
解:(1)由直线l及圆C的方程消去y可得:(1+k2)x2+(2k-4)x-4=0①,(1¢)
∵D=(2k-4)2+16(1+k2)>0,(2¢)
∴对任意实数k,直线l与圆C有两个不同的交点;(3¢)
(2)经配方得,(x-2)2+y2=9,所以,
圆C的圆心C的坐标是(2,0),半径r=3,所以,当k=2时,
点C到直线l的距离为![]() ,(5¢)
,(5¢)
故AB=![]() ;(6¢)
;(6¢)
(3)设两交点A、B的坐标分别为(x1,y1),(x2,y2),A、B的中点P的坐标分别为(x0,y0),(7¢)则
由①可得,![]() ②,(8¢)又由kx0-y0+1=0可得
②,(8¢)又由kx0-y0+1=0可得![]() ③,(9¢)
③,(9¢)
将③代入②并化简可得![]() ,
,
故所求的轨迹方程为x2+y2-2x-y=0.(10¢)
第一学段模块考试
高一年级数学必修2试卷
高一数学第一模块结业考试试题(第Ⅱ卷)
| 题号 | 一 | 二 | 三 | 总分 | |||
| 21 | 22 | 23 | 24 | ||||
| 得分 | |||||||
一、选择题(请将正确答案写在下表空格内)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | A | B | B | C | C | A | D | A | D | B | D | C | B | B | A | D |
二、填空题(请将正确答案写在下列横线上)
17、 2 ;18、(x+1)2+(y-2)2=4;19、 ![]() ;20、
①
③ .
;20、
①
③ .
三、解答题:(本大题共4小题,每小题10分,共40分)
21、已知A(1,0)、B(0,1)、C(-3,-2)三点.
(1)试判断三角形ABC的形状;
(2)求三角形ABC的面积.
解:(1)kAB=-1,kBC=1,(2¢)kAB×kBC=-1,∴AB^BC,(4¢)
∴三角形ABC是直角三角形. (5¢)
(2)![]() ,
,![]() (8¢)
(8¢)
∴三角形ABC的面积为
![]() (平方单位). (10¢)
(平方单位). (10¢)
 22、如图,在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为450,求:
22、如图,在长方体AC¢中,已知底面两邻边AB和BC的长分别为3和4,对角线BD¢与平面ABCD所成的角为450,求:
(1)长方体AC¢的高;
(2)长方体AC¢的表面积;
(3)几何体C¢D¢-ABCD的体积.
解:(1)连结BD,∵DD¢^平面ABCD,
∴Ð DBD¢是直线BD¢与平面ABCD所成的角.
∴Ð DBD¢=450,(2¢)∴DD¢= BD,
又AB=3,BC=4,∴DD¢= BD=5,
∴长方体AC¢的高为5.(4¢)
(2)长方体AC¢的表面积S=2(3´4+4´5+5´3)=94(平方单位)(7¢)
(3)几何体C¢D¢-ABCD的体积V=![]() (3´4´5)=30(立方单位). (10¢)
(3´4´5)=30(立方单位). (10¢)
 23、如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
23、如图,DABC是直角三角形,ÐABC=900,AP^平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
(1)当DE//BC时,求证:直线PB^平面ADE;
(2)当DE^PC时,求证:直线PC^平面ADE;
(3)当AB=BC时,求二面角A-PC-B的大小.
(1)证:∵AP=AB,点D是PB的中点,∴AD^PB,
∵AP^平面ABC,BCÌ平面ABC,
∴AP^BC,∵AB^BC,∴BC^平面PAB,
∵PBÌ平面PAB,∴BC^PB,
∵DE//BC,∴DE^PB,∴PB^平面ADE. (3¢)
(2)证:∵BC^平面PAB,ADÌ平面PAB,∴BC^AD,
又AD^PB,∴AD^平面PBC,∵PCÌ平面PBC,∴AD^PC,
又DE^PC,∴PC^平面ADE. (6¢)
(3)由(2)可知,当DE^PC时,PC^平面ADE,
∴ÐAED是二面角A-PC-B的平面角. (7¢)
设AP=a,则AB=BC=a,![]() ,
,![]() ,(8¢)
,(8¢)
∵AD^平面PBC,DEÌ平面PBC,∴AD^DE,
在RtDADE中,可求得,![]() ,
,![]() ,(9¢)
,(9¢)
∴![]() ,∴ÐAED=600,
,∴ÐAED=600,
∴二面角A-PC-B的大小为600. (10¢)
24、已知直线l :kx-y+1=0,圆C:x2+y2-4x-5=0,
(1)求证:无论k取任何实数,直线l与圆C恒有两个不同的交点;
(2)当k=2时,直线l与圆C相交于A、B,求A、B两点间的距离;
(3)当实数k变化时,求直线l被圆C截得的弦的中点的轨迹方程.
解:(1)由直线l及圆C的方程消去y可得:(1+k2)x2+(2k-4)x-4=0①,(1¢)
∵D=(2k-4)2+16(1+k2)>0,(2¢)
∴对任意实数k,直线l与圆C有两个不同的交点;(3¢)
(2)经配方得,(x-2)2+y2=9,所以,
圆C的圆心C的坐标是(2,0),半径r=3,所以,当k=2时,
点C到直线l的距离为![]() ,(5¢)
,(5¢)
故AB=![]() ;(6¢)
;(6¢)
(3)解法一:设两交点A、B的坐标分别为(x1,y1),(x2,y2),A、B的中点P的坐标分别为(x0,y0),(7¢)则
由①可得,![]() ②,(8¢)又由kx0-y0+1=0可得
②,(8¢)又由kx0-y0+1=0可得![]() ③,(9¢)
③,(9¢)
将③代入②并化简可得![]() ,
,
故所求的轨迹方程为x2+y2-2x-y=0.(去掉原点)(10¢)
(3)解法二:设两交点A、B的中点P的坐标分别为(x0,y0),(7¢)则
由PC^AB,可得,![]() ②,(8¢)
②,(8¢)
又由kx0-y0+1=0③,(9¢)
将②代入③并化简可得![]() ,
,
故所求的轨迹方程为x2+y2-2x-y=0. (去掉原点)(10¢)
说明:没说明“去掉原点”不扣分.
 A.
A. 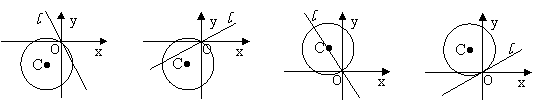 A.
A.