第一学期第二学段
高一年级数学必修四模块考试试题
|
答题注意事项：
1.本试卷满分150分，第Ⅰ卷17道题，满分100分，
第Ⅱ卷7道题，满分50分，全卷共24道题；
2.考试用时120分钟；
3.答题时请将答案写在试卷的相应位置上.
第Ⅰ卷(满分100分)
一、选择题 本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有
一项符合题目的要求，请将答案填写在题后的表格中．
1．已知点P（
）在第三象限，则角
在
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．函数
，
是
A．最小正周期为
的奇函数 B．最小正周期为的偶函数
C．最小正周期为
的奇函数 D．最小正周期为的偶函数
3．已知
与
均为单位向量，它们的夹角为
，那么
等于
A．
B．
C．
D．4
4．已知M是△ABC的BC边上的中点，若向量
=a,
= b，则向量
等于
A．
(a－b) B．(b－a)
C．( a＋b) D．
(a＋b)
5．若
是△
的一个内角，且
，则
的值为
A．
B．
C．
D．
6．已知
，则
的值是
A．－1 B．1 C．2 D．4
7．在
中，有如下四个命题：①
； ②
；
③若
，则为等腰三角形；
④若
，则为锐角三角形．其中正确的命题序号是
A．① ② B．① ③ ④ C．② ③ D．② ④
8．函数
在一个周期内的图象如下，此函数的解析式为
A．
B．
C．
D．
9．下列各式中，值为
的是
A．
B．
C．
D．
10．已知
为锐角，且cos
=
,cos
=
，则
的值是
A．
B．
C．
D．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题 本大题共4小题，每小题5分，共20分．请将答案填写在横线上．
11．
的值为
．
12．已知向量
．若向量
，则实数
的值是 ．
13．若
, 且
, 则
的值是____________．
14．已知
，
，则
的值为 ．
三、解答题 本大题共３小题，每小题10分，共30分．解答应写出文字说明，证明过程
或演算步骤．
15．(本题满分10分)已知
，当
为何值时，
平行时它们是同向还是反向？
16．(本题满分10分) 已知函数
，．
（Ⅰ）求
的最大值；
（Ⅱ）若
，求
的值.
17．(本题满分10分) 已知函数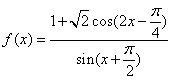
．
（Ⅰ）求
的定义域；
（Ⅱ）若角是第四象限角，且
，求
．
第Ⅱ卷(满分50分)
一、选择题 本大题共2小题，每小题5分，共10分．在每小题给出的四个选项中，只有
一项符合题目的要求，请将答案填写在题后的【 】中．
18．已知tan(α+β) =
, tan(β－
)=
,那么tan(α+ )为
【 】
A．
B．
C．
D．
19．
的值为
【 】
A．
B．
C．
D．
二、填空题 本大题共2小题，每小题5分，共10分．请将答案填写在横线上．
20．
的值为
．
21．已知
＝2，则的值为
；
的值为
．
三、解答题 本大题共３小题，每小题10分，共30分．解答应写出文字说明，证明过程
或演算步骤．
22．(本题满分10分) 已知函数
，
，那么
（Ⅰ）函数的最小正周期是什么？
（Ⅱ）函数在什么区间上是增函数？
23．(本题满分10分)已知向量 
=（cos，sin），
=（cos，sin），
｜＝
．
（Ⅰ）求cos（－）的值；
（Ⅱ）若０＜＜
，－＜＜０，且sin＝－
，求sin的值．
24．(本题满分10分)
| |
，求
（Ⅰ）
；
（Ⅱ）若
的最小值是
，求实数的值．
益田中学2007—2008学年度第一学期第二学段
高一年级 数学必修四 模块考试试题
参考答案
（一）本套试题命题范围：
1.使用教材（人教A版）
2.命题范围（必修4 全册）
3.适用学生（高一年级）
（二）详细答案及评分标准：
第Ⅰ卷(满分100分)
一、 选择题 本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项符合题目的要求，请将答案填写在题后的表格中．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | A | C | D | C | Ｃ | A | D | B |
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题 本大题共4小题，每小题5分，共20分．请将答案填写在横线上．
11．
12. 
13．
14．
三、解答题 本大题共３小题，每小题10分，共30分．解答应写出文字说明，证明过程或演算步骤．
15．(本题满分10分)
解: 因为
，
--------------------------------2分
当
时，
则
-------------------------------------------------2分
解得：
--------------------------------------------------------------------------2分
此时，
=
=
=
．-----------------------------------------------------------2分
所以
反向．---------------------------------------------------------------2分
［另解：当，存在唯一实数，使
即
得：
解得：
， 即当
，
这时因为
，所以反向．］
16．(本题满分10分)
解:（Ⅰ）（5分） 
=
-----------------------------------1分
------------------------------2分
∴的最大值为
．--------------------------------2分
（Ⅱ）（5分） 因为
，即
-------------------1分
∴
--------------------------------------2分
∴
．------------------------------------------2分
17．(本题满分10分)
解：（Ⅰ）（4分）由
，得
，
所以f(x)的定义城为
．--------------------------------4分
[另解：由，得
∴
所以f(x)的定义城为
］
（Ⅱ）（6分）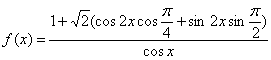
＝
-----------------------------------------------------------1分
∴
．---2分
因为是第四象限角，所以
．----------2分
所以
．----------------------------------------------------------------1分
第Ⅱ卷(满分50分)
一、选择题 本大题共2小题，每小题5分，共10分．在每小题给出的四个选项中，只有一项符合题目的要求，请将答案填写在题后的【 】中．
18．C 19．D
二、填空题 本大题共2小题，每小题5分，共10分．请将答案填写在横线上．
20．
21．
（2分）； 
（3分）。
三、解答题 本大题共３小题，每小题10分，共30分．解答应写出文字说明，证明过程或演算步骤．
22．(本题满分10分)
解：（Ⅰ）（5分）
＝
＝1+
=
-------------------------------------------------2分
=
,---------------------------------------------------2分
∴函数的最小正周期是π．--------------------------------------1分
（Ⅱ）（5分） 由
，
---------------------------2分
得 
--------------------------------------------------------2分
∴函数的增区间为：
--------------------------------1分
23．(本题满分10分)
解：（Ⅰ）（5分） 
，
．
---------------------------------------1分
，
．---------------------------------2分
即 
．
---------------------------------------------------1分
．
------------------------------------------------------------------1分
（Ⅱ）（5分）∵
， ∴ 
---------------------1分
∵ 
，∴ 
----------------------------------1分
∵ 
，∴ 
-----------------------------------------------------1分
∴
．-----------------------------------------------------------2分
24．(本题满分10分)
解：（Ⅰ）（5分） a·b=
------------------2分
a+b=
-----2分
∵
， ∴
∴ a+b=2cosx.-----------------------------------------------------------------------1分
（Ⅱ）（5分） 
即
------------------------------------------------2分
∵， ∴
时，当且仅当
取得最小值－1，这与已知矛盾．
时，当且仅当
取最小值
由已知得
，解得
时，当且仅当
取得最小值
由已知得
，解得
，这与
相矛盾．
综上所述，
为所求．-------------------------------------------------------3分