高一年级数学第一学期期中考试试题
命题单位:无锡市荡口中学 出卷人:谢晓丰 审核人:浦春玲
一、选择题(本大题共8题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、已知集合![]() 则
则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.R
D.R
2、下列各组函数中,两个函数相等的一组是 ( )
A、f(x)=x0与g(x)=1
B、f(x)=x-1与g(x)=![]()
C、f(x)=x2与g(x)=![]() D、f(x)=x2与g(x)=
D、f(x)=x2与g(x)=![]()
3、下列说法不正确的是 ( )
A.若M是N的子集,则N一定不是M的子集
B.若![]() ,则实数a、b、c至少有一个不为0
,则实数a、b、c至少有一个不为0
C.若![]() ,则y>0
,则y>0
D.若a>2,b>2,则a+b>4
4、将函数![]() 的图像向右平移3个单位再向下平移2个单位所得图像的函数解析式为
的图像向右平移3个单位再向下平移2个单位所得图像的函数解析式为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、映射f:A→B,在f作用于A中元素(x,y)与B中元素(x-1,3-y)对应,则与B中元素(0,1)对应的A中元素是 ( )
A、(-1,2) B、(0,3) C、(1,2) D、(-1,3)
6、2x+x=0在下列哪个区间内有实数解 ( )
A、[-2,-1] B、[0,1] C、[1,2] D、[-1,0]
7、设a>1,实数x,y满足f(x)=ax,则函数f(x)的图象形状 ( )
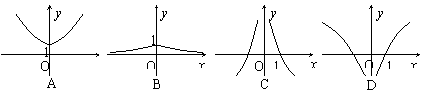
8、若x∈R,n∈N*,定义Exn=x(x+1)(x+2)……(x+n-1),例如:![]() =(-4)·(-3)·(-2)·(-1)=24,则f(x)=x·
=(-4)·(-3)·(-2)·(-1)=24,则f(x)=x·![]() 的奇偶性为
(
)
的奇偶性为
(
)
A、为偶函数不是奇函数 B、是奇函数不是偶函数
C、既是奇函数又是偶函数 D、非奇非偶函数
二、填空题(本大题共10小题,每小题5分,共50分,把答案填在题中横线上)
9、设U=R,集合A={x-5<x<5},B={x0≤x<7},则A∪(CuB)= 。
10、三个数60.7,0.76,log0.76的从小到大的关系是 。
11、设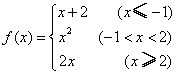 ,若
,若![]() ,则
,则![]() 。
。
12、已知指数函数f(x)=ax的图像经过点(3,8),则![]() 的值为____________。
的值为____________。
13、求函数![]() (1
(1![]() 4)的最大值和最小值分别是
。
4)的最大值和最小值分别是
。
![]() 14、如果函数在区间
14、如果函数在区间![]() 上是递增的,那么实数
上是递增的,那么实数![]() 的取值范围是
。
的取值范围是
。
15、函数f(x)为R上的奇函数,且当x<0时 , f(x) =- x2-1, 则当x∈R时, f(x)= 。
16、若11.2a=1000,0.0112b=1000,则![]() =
。
=
。
17、已知实数a,b满足等式log2a=log3b,给出下列5个关系式:①a>b>1;②b>a>1;
③a<b<1;④b<a<1;⑤a=b.其中可能成立的关系式是____________。(填序号)
18、函数f(x)=![]() (常数α∈Z)为偶函数且在(0,+∞)是减函数,则f(2)= 。
(常数α∈Z)为偶函数且在(0,+∞)是减函数,则f(2)= 。
三、解答题(本大题共5小题,解答应写出必要的文字说明,证明过程或演算步骤)
19、(本题12分)计算:(1)![]()
![]()
(2)![]() ÷
÷![]()
20、(本题14分)已知A={0,-4},B={xx2+2(a+1)x+a2=1},若A∪B=A,求a的值。
21、(本题14分)已知函数f(x)=![]() ,其中a(a>0,a≠1)为常数。
,其中a(a>0,a≠1)为常数。
⑴求函数f(x)的定义域;⑵证明f(x)是奇函数;⑶判断函数f(x)在定义域上的单调性并加以证明。
22、(本题14分)某市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同。甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元。小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时。
(1)设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元
元![]() ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元
元![]() 。试求
。试求![]() 和
和![]() ;
;
(2)问:小张选择哪家比较合算?为什么?
23、(本题16分)已知![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() (其中
(其中![]() 且
且![]() )。
)。
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)解关于![]() 的不等式
的不等式![]() ,结果用集合或区间表示。
,结果用集合或区间表示。
2007—2008学年度第一学期期中考试高一年级数学试题答案
一、选择题:每小题5分
1、B 2、D 3、A 4、C 5、C 6、D 7、A 8、A
二、填空题:每小题5分
9、(-∞,5)∪[7,+∞] 10、![]() <0.76<60.7
<0.76<60.7
11、![]() 12、
12、![]() 13、
13、![]() ,
,![]() 14、a≥-3
14、a≥-3
![]() 15、 -x2-1 x<0
15、 -x2-1 x<0
f(x)= 0 x=0
x2+1 x>0
16、1 17、②④⑤
18、![]()
三、解答题:
19、⑴解:原式=![]()
=![]() …………………………3分
…………………………3分
=![]() =0………………………………6分
=0………………………………6分
⑵解:原式=![]() ……………………………8分
……………………………8分
=4a1b0=4a…………………………………12分
20、解:∵A∪B=A
∴B![]() A ……………………………………1分
A ……………………………………1分
(1)当B=![]() 时, △<0得a<-1…………………3分
时, △<0得a<-1…………………3分
(2)当B={0}时,
![]()
![]()
![]() △=0
4(a+1)2-4(a2-1)=o …………4分
△=0
4(a+1)2-4(a2-1)=o …………4分
a2=1 a=±1
![]()
![]() a=-1 a=-1
a=-1 a=-1![]() ………………………6分
………………………6分
a=±1
(3)当B={-4}时 ……………………………………8分
![]()
![]()
![]()
![]() △=0
a=-1
无解
……9分
△=0
a=-1
无解
……9分
16-8(a+1)+a2-1=0 a=7或1
(4)当B={0,-4}时
![]()
![]() △>0
△>0
△>0
△>0
![]()
![]() -2(a+1)=-4
a=1
a=1 …………13分
-2(a+1)=-4
a=1
a=1 …………13分
a2-1=0 a=±1
∴综上所述:a=1 或a≤-1…………………………………………14分
21、解(1)(1-x)/(1+x)>0 得-1<x<1 …………2分
定义域:(-1,1) ………………………… 3分
(2)定义域关于原点对称,又![]() ∴f(x)为奇函数 ……5分
∴f(x)为奇函数 ……5分
(3)a>1时f(x)在(-1,1)上是增函数,0<a<1时f(x)在(-1,1)上是减函数…7分
证明:设![]()
![]() >0
>0
![]() ………………………………………………10分
………………………………………………10分
当a>1时,![]()
当0<a<1时有![]() ………………………………12分
………………………………12分
∴a>1时f(x)在(-1,1)上是减函数,0<a<1时f(x)在(-1,1)上是增函数…14分
22、(1)![]() ……………………2分
……………………2分
![]() ………………5分
………………5分
(2)由![]() 得
得![]() 或
或![]() 即
即
![]() 或
或![]() (舍) ……………………7分
(舍) ……………………7分
当![]() 时,
时, ![]() ,∴
,∴![]() 即选甲家……9分
即选甲家……9分
当![]() 时,
时, ![]() 即选甲家也可以选乙家。……10分
即选甲家也可以选乙家。……10分
当![]() 时,
时,![]() ,∴
,∴![]() 即选乙家.11分
即选乙家.11分
当![]() 时,
时,![]() ,
,
∴![]() 即选乙家.…………………………………………13分
即选乙家.…………………………………………13分
综上所述:当![]() 时,选甲家;
时,选甲家;
当![]() 时,选甲家也可以选乙家;
时,选甲家也可以选乙家;
当![]() 时,选乙家. ………………………14分
时,选乙家. ………………………14分
23、已知![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() .
.
其中![]() 且
且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)解关于![]() 的不等式
的不等式![]() ,结果用集合或区间表示.
,结果用集合或区间表示.
解:
(1)因![]() 是奇函数,所以有
是奇函数,所以有![]() ,所以
,所以![]() =0. ……4分
=0. ……4分
(2)当![]() 时,
时,![]()
![]() …………………………………6分
…………………………………6分
由![]() 是奇函数有,
是奇函数有,![]() ,
,![]()
![]() …………………………8分
…………………………8分
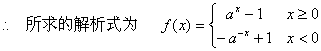 …………10分
…………10分
(3)不等式等价于
![]() 或
或![]()
即![]() 或
或![]() …………………………12分
…………………………12分
当![]() 时,有
时,有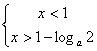 或
或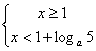 ,注意此时
,注意此时![]() ,
,
可得此时不等式的解集为![]() ……………………14分
……………………14分
同理可得,当![]() 时,不等式的解集为R . (或由此时函数的值域为
时,不等式的解集为R . (或由此时函数的值域为![]() 得)……………………………………………………………………15分
得)……………………………………………………………………15分
综上所述,当![]() 时,不等式的解集为
时,不等式的解集为![]() ;
;
当![]() 时,不等式的解集为R .…………………………16分
时,不等式的解集为R .…………………………16分