高一年级数学第一学期期末考试试卷
满分 100分 时间 100分钟
一、填空题(共12题,36分)
1. 设全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() __________________
__________________
2.已知![]() ,则
,则![]() ______________
______________
3.函数![]() 是________函数。(填奇偶性)
是________函数。(填奇偶性)
4.函数![]() 的单调增区间为__________________.
的单调增区间为__________________.
5.集合![]() 为函数
为函数![]() 的定义域,集合
的定义域,集合![]() 为函数
为函数![]() 的值域,则
的值域,则![]() =___________________
=___________________
6.已知函数![]() ,则
,则![]() _______________
_______________
7.函数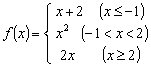 ,且
,且![]() ,则
,则![]() 的值是______________
的值是______________
8.已知函数![]() 且
且![]() 的图像恒过定点P,则P点的坐标是______________
的图像恒过定点P,则P点的坐标是______________
9.已知点![]() 在幂函数
在幂函数![]() 的图像上,点
的图像上,点![]() 在幂函数
在幂函数![]() 的图像上,若
的图像上,若![]() ,则
,则![]() _______________
_______________
 10.已知二次函数
10.已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且不等式
,且不等式![]() 的解集为
的解集为![]() ,若
,若![]() 的最大值为正数,则实数
的最大值为正数,则实数![]() 的取值范围是____________
的取值范围是____________
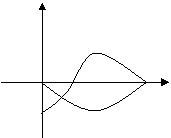
11.已知![]() 是偶函数,
是偶函数,![]() 是奇函数,它们的定义域都是
是奇函数,它们的定义域都是![]() ,且它们在
,且它们在![]() 上的图像如右图所示,则不等式
上的图像如右图所示,则不等式![]() 的解集为_______________
的解集为_______________
12. 下列四个命题中:
(1)如果两个函数都是增函数,那么这两函数的积运算所得函数为增函数;
(2)奇函数![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 在
在![]() 上为增函数;
上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数的最小值是![]() ,最大值为
,最大值为![]() ,则其值域为
,则其值域为![]() .
.
其中假命题的序号为_____________
二、选择题:(共4题,12分)
13.函数![]() (常数
(常数![]() )的图像所经过的象限是
)的图像所经过的象限是 ![]()
A. 第一、二、三象限 B. 第一、三、四象限
C. 第一、二、四象限 D. 第二、三、四象限
14.函数![]() 在闭区间
在闭区间![]() 上有最大值8,则实数
上有最大值8,则实数![]() 的值不可能的是
的值不可能的是
![]()
A. 0 B.
15.已知函数![]() 的定义域是
的定义域是![]() ,那么
,那么![]() 的定义域是
的定义域是 ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
16.《中华人民共和国个人所得税法》规定,个人每月的工资收入中不超过1600元的部分为免税收入,超过1600元的部分为应纳税收入;此项税款按下表分段累进计算。
| 应纳税收入额(元) | 税率(%) |
|
| 5 |
|
| 10 |
|
| 15 |
| …… | …… |
某人一月份缴纳此项税款![]() 元,则他当月的工资收入介于
元,则他当月的工资收入介于 ![]()
A. 1600元至1800元 B. 1800元至2000元
C. 2000元至2500元 D. 2500元至3600元
三、解答题:(共6题,52分)
17.(6分)已知函数![]() ,函数
,函数![]() ,设M为函数
,设M为函数![]() 的最小值,N为函数
的最小值,N为函数![]() 的最小值,比较M和N的大小
的最小值,比较M和N的大小
18.(8分)已知函数![]() ,
,
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)若![]() ,求
,求![]() 的值域
的值域
19.(8分)已知幂函数![]()
![]() 的图像关于
的图像关于![]() 轴对称,且在区间
轴对称,且在区间![]() 为减函数
为减函数
(1)求![]() 的值和函数
的值和函数![]() 的解析式
的解析式
(2)解关于![]() 的不等式
的不等式![]() ,
,
20.(8分)10辆货车从A站出发以时速![]() 千米/小时,匀速驶往相距400千米的B站,为安全起见,要求每辆货车的间隔等于
千米/小时,匀速驶往相距400千米的B站,为安全起见,要求每辆货车的间隔等于![]() 千米(
千米(![]() 为常数,货车长度忽略不计),
为常数,货车长度忽略不计),
(1)将第一辆货车由A站出发到最后一辆货车到达B站所需的时间![]() 表示成时速
表示成时速![]() 的函数;
的函数;
(2)若![]() ,则货车的时速为多少时,(1)中所需的时间
,则货车的时速为多少时,(1)中所需的时间![]() 最短?最短时间为多少?
最短?最短时间为多少?
21.(10分)已知函数![]()
(1)当![]() 时,求证函数
时,求证函数![]() 在它的定义域上单调递减
在它的定义域上单调递减
(2)是否存在实数![]() 使得区间
使得区间![]() 上一切
上一切![]() 都满足
都满足![]()
![]()
![]() ,若存在,求实数
,若存在,求实数![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
22.(12分)已知函数![]() 的定义域为
的定义域为![]() ,且同时满足:①
,且同时满足:①![]() ;②
;②![]() 对一切
对一切![]()
![]() 恒成立;③若
恒成立;③若![]() ,
,![]() ,
,![]() ,则有
,则有![]()
(1)求![]() 的值
的值
(2)设![]()
![]() ,且
,且![]() ,求证:
,求证:![]()
(3)试比较![]() 与
与![]() (
(![]() )的大小;
)的大小;
(4)某同学发现,当![]() (
(![]() )时,有
)时,有![]() ,由此他提出猜想:对一切
,由此他提出猜想:对一切![]()
![]() ,都有
,都有![]() ,请你判断此猜想是否正确,并说明理由。
,请你判断此猜想是否正确,并说明理由。
答案:
一、填空题
1、![]() ;2、
;2、![]() ;3、奇;4、
;3、奇;4、![]() ;5、
;5、![]() ;
;
6、![]() ;7、
;7、![]() ;8、
;8、![]() ;9、
;9、![]() ;10、
;10、![]() ;11、
;11、![]() ;
;
12、(1)、(3)、(4);
二、选择题
13、B;14、D;15、D;16、C;
三、简答题
17、![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() 。
。
18、(1)非奇非偶;
(2)![]()
19、(1)![]() ;(2)
;(2)![]()
![]()
20、(1)![]() ;(2)当时速为80千米/小时,最短时间为10小时;
;(2)当时速为80千米/小时,最短时间为10小时;
21、(1)![]() 时,定义域为
时,定义域为![]() ;
;![]() 定义域为
定义域为![]() ;
;![]() 时,定义域为
时,定义域为![]() ;
;![]() 时,
时,![]() ;
;![]() 时,定义域为R。
时,定义域为R。
(2)![]() ;
;
22、(1)略;(2)![]() ;(3)恒成立;
;(3)恒成立;