高一数学集合与简易逻辑章节测试
班级： 姓名： 成绩：
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题4分，共40分）（注意：请将答案写在第二张答题卡上）.
1.下列关于集合的说法正确的是（ C ）
A. {1}Í{（1，2）}
B. Æ没有子集
C. 设U为全集,则(CUA)
A=Æ
D. {(a,b)}={(b,a)}
2. 不等式
的解集为（ D ）
A. 
B. 
C. 
D.
3、下列命题：①
；②“若x2+y2=0,则x,y全为0”的否命题，③命题“全等三角形是相似三角形”的逆命题；④“圆内接四边形对角互补”的逆否命题，其中真命题的个数是
（ C ）
A.1个 B.2个 C.3个 D.4个
4、已知集合
，集合
，
，则（ C ）
A．U=A∪B B．U=(CuA)∪B
C． U=A∪(CuB) D．U=(CuA)∪(CuB)
5、若x∈R，则x>1的一个必要不充分条件是（ B ）
A．x>1 B.x>0 C．x>2 D．x≥2
6、若非空集合A={x2a+1≤x≤3a-5 }，B={x3≤x≤22}，则能使
成立的所有a的集合是
（ C ）
A.{a1≤a≤9} B.{a6≤a≤9} C.{aa≤9} D.Æ
7、设甲、乙、丙是三个命题，如果甲是乙的必要条件，丙是乙的充分不必要条件，那么丙是甲的 （ A ）
A.充分不必要条件 B.充要条件
C.必要不充分条 D.既不充分也不必要条件
8、设全集为I,下列条件①A∪B=A;②(CIA)∩B=f;③A∪(CIB)=I④CIAÍCIB.其中是BÍA的充要条件的是( A )
A. ①②③④ B. ①②④
C. ①④ D. ②③
9、不等式
的解集是
,则
( D )
A.10 B.-10 C.14 D.-14
10、命题”在△ABC中,若∠A=90°,则∠B,∠C全为锐角”的否命题为( D )
A. 在△ABC中,若∠A=90°, 则∠B,∠C全不是锐角
B. 在△ABC中,若∠A≠90°,则∠B,∠C不一定为锐角
C. 在△ABC中,若∠A≠90°,则∠B,∠C有一个不是锐角
D. 在△ABC中,若∠A≠90°,则∠B,∠C不全是锐角
高一第一章 集合与简易逻辑章节测试
班级：_____姓名：______ 成绩：____
一、 选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | C | C | B | C | A | A | D | D |
二、填空题：本大题共4小题；每小题4分，共20分，把答案填在题中的横线上。
11、全集U={x x是小于9的正整数}.A={1,2,3} ,B={3,4,5,6}则CU(A
B)= {7，8}。
12、已知集合{x∈Rmx2+2x+1=0}中恰有2个元素，则实数m的取值范围是m<1且m≠0。
13.判断下列说法：
①“x2=y2”是“x=y”的充分不必要条件；
②“a2≠b2”是“a≠b或a≠-b”的充要条件；
③ 若p且q是真命题，则p或q 必是真命题；
④“若c<0,则x2+2x+c=0有实根”的否命题是假命题；
⑤“若x>3则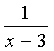
>0”的否命题是“若x
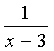3则<0”
其中正确说法的序号是③、④.
14、已知
，
，则p是q的必要不充分条件.
15、对任意实数x，若不等式x+1-x-2>k恒成立，则k的取值范围是 k<-3。
三、解答题：本大题共4小题，共60分，解答应写出文字说明、证明过程或推演步骤。
16、（本小题满分12分）分别写出由下列各命题构成的“p或q”，“p且q”，“非p”形式的复合命题,并判断复合命题的真假:
(1) p：6是12的约数；q：8是12的约数；
(2)菱形的对角线相等；q：菱形的对角线互相垂直平分；
解：（1）“p或q”：6是12的约数或8是12的约数。 真命题
“p且q”：6是12的约数且8是12的约数。 假命题
“非p”：6不是12的约数 假命题
（2）“p或q”：矩形的对角线相等或互相垂直平分。 真命题
“p且q”：矩形的对角线相等且互相垂直平分。 假命题
“非p”：矩形的对角线不相等。 假命题
17、（本小题满分6+8+10=24分）解关于x的不等式或不等式组：
（1）
解：整理得：
∵方程
的两根为-1/2、2。
∴不等式的解集为：{x-1/2<x<2}
（2） 
解：∵方程
的两根为2a、a+1,
∴① 2a≥a+1即a≥1时，不等式的解集为：
{x a+1≤x≤2a }
② 2a<a+1即a<1时，不等式的解集为：
{x 2a≤x≤a+1 }
（3） 
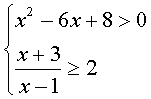
解：解不等式
……(ⅰ)
得：{xx<2或x>4}
解不等式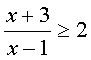
……(ⅱ)
整理得：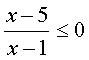
它等价于(Ⅰ)
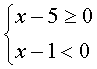或(Ⅱ)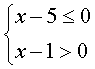
解(Ⅰ)得:x∈Æ;解(Ⅱ) 得:{x1<x≤5}
∴不等式(ⅱ) 的 解集为(Ⅰ) ∪(Ⅱ)= {x1<x≤5}
∴不等式的 解集为(ⅰ) ∪(ⅱ)= {xx<2或x>4}∪{x1<x<5}={x1<x<2或4<x≤5}
18、（本小题满分12分）已知集合
,若
,求实数p的取值范围。
解:化简集合
={x-2<x<5}
∵
∴(1)B=Æ即: p+1>2p-1
p
<2 时成立.
(2) B≠Æ时只须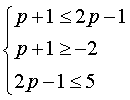
∴2≤p≤3
综上所述p的取值范围是:
{p p <2或2≤p≤3}={p p≤3}
19、（本小题满分12分）
已知
有两个不相等的负根，
无实根，若“p或q”为真，“p且q”为假，求
的取值范围。
解:记p、q的解集分别为A、B。
∵
有两个不相等的负根，
∴
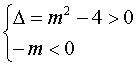Þ
∴
无实根，
∴
Þ
∴
∵“p或q”为真，“p且q”为假
∴p,q中仅有一个为真。
∴（1）p真且q假，即
∩
=
（2）p假且q真，即
∩
=
综上所述m的取值范围是
(1)∪(2)=∪
=
附加题20、（本小题满分10分）
已知三个关于 
的方程：
，
，
中至少有一个方程有实数根，求实数a的取值范围．
解：设上述三个方程都没有实数根a的取值范围记作集合A，则所求实数a的取值范围为集合
。
而三个方程都没有实数根的充要条件是；
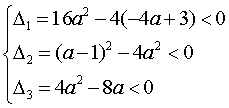
解这个不等式组：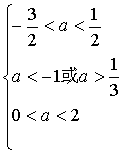
Þ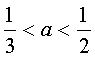
∴A={a}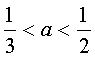
∴
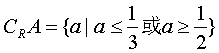
∴三个方程中至少有一个方程有实数根，实数a的取值范围是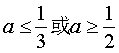
。