集合练习题
1.已知集合![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.1 B.—1 C.1或—1 D.1或—1或0
2.设集合![]() ,
,![]() ,若
,若![]() ,则k的取值范围( )
,则k的取值范围( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.如图,U是全集,M、P、S是U的3个子集,则阴影部分所表示的集合是 ( )
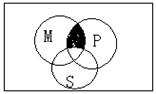 A、
A、 ![]() B、
B、 ![]()
C、 ![]() D、
D、 ![]()
4.设![]() ,
,![]() ,若
,若![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.函数![]() 的定义域为( )
的定义域为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6. 设![]() ,若
,若![]() ,则a=__________。
,则a=__________。
7.已知集合![]() {1,2},
{1,2},![]() {
{![]() },则集合B=
.
},则集合B=
.
8.已知集合![]() 那么集合
那么集合![]() =
=
9.50名学生做的物理、化学两种实验,已知物理实验做的正确得有40人,化学实验做的正确的有31人,两种实验都做错的有4人,则这两种实验都做对的有 人.
10.已知集合![]() ,其中a,d,
,其中a,d,![]() ,若A=B,求q的值。
,若A=B,求q的值。
11.已知全集U=![]() ,若A=
,若A=![]() ,
,![]() ,求实数的a ,b值
,求实数的a ,b值
12.若集合S=![]() ,
,![]() 且S∩T=
且S∩T=![]() ,P=S∪T,求集合P的所有子集
,P=S∪T,求集合P的所有子集
13.已知集合A=![]() ,B={x2<x<10},C={x x<a},全集为实数集R.
,B={x2<x<10},C={x x<a},全集为实数集R.
(1) 求A∪B,(CRA)∩B;(2) 如果A∩C≠φ,求a的取值范围。
14.已知方程![]() 的两个不相等实根为
的两个不相等实根为![]() 。集合
。集合![]() ,
,
![]() {2,4,5,6},
{2,4,5,6},![]() {1,2,3,4},A∩C=A,A∩B=
{1,2,3,4},A∩C=A,A∩B=![]() ,求
,求![]() 的值?
的值?
15.已知集合![]() 的元素全为实数,且满足:若
的元素全为实数,且满足:若![]() ,则
,则![]() 。
。
(1)若![]() ,求出
,求出![]() 中其它所有元素;
中其它所有元素;
(2)0是不是集合![]() 中的元素?请你设计一个实数
中的元素?请你设计一个实数![]() ,再求出
,再求出![]() 中的所有元素?
中的所有元素?
(3)根据(1)(2),你能得出什么结论。
答案
(1)---(5) DBCDA
(6)2 (7)![]() (8)
(8)![]() (9)25
(9)25
(10)解:由元素的互异性可知:![]() ,
,![]() ,
,![]() ,
,
而集合A=B,则有:
![]() ① 或
① 或 ![]() ②
②
由方程组①解得:![]() (舍去)
(舍去)
由方程组②解得:![]() (舍去),或
(舍去),或![]()
所以![]()
(11)解:由补集的定义可知:![]() 且
且![]() ,
,
所以![]() 且
且![]() .
.
解得![]()
所以所求 ![]() ,
,![]() 的值为
的值为![]()
(12)解:由S=![]() 且S∩T=
且S∩T=![]() 得
得![]()
则![]() ,而S=
,而S=![]()
当![]() 时,
时,![]()
即![]() 满足S∩T=
满足S∩T=![]()
当![]() 时,
时,![]()
即![]() 不满足S∩T=
不满足S∩T=![]()
所以![]() ∪
∪![]() 那么
那么![]() 的子集有:
的子集有:
![]()
(13解:(1)∵A=![]() ,B={x2<x<10},∴A∪B={x2<x<10};
,B={x2<x<10},∴A∪B={x2<x<10};
(2) ∵A=![]() ,∴CRA={x x<3或x≥7}
,∴CRA={x x<3或x≥7}
∴(CRA)∩B={x x<3或x≥7}∩![]() ={x2<x<3或7≤x<10}
={x2<x<3或7≤x<10}
![]() (3)如图,
(3)如图,
∴当a>3时,A∩C≠φ
(14).解:由A∩C=A知A![]() C。又
C。又![]() ,则
,则![]() ,
,![]() . 而A∩B=
. 而A∩B=![]() ,故
,故![]() ,
,![]() 。显然即属于C又不属于B的元素只有1和3. 不仿设
。显然即属于C又不属于B的元素只有1和3. 不仿设![]() =1,
=1,![]() =3. 对于方程
=3. 对于方程![]() 的两根
的两根![]() 应用韦达定理可得
应用韦达定理可得![]() .
.
(15).解:(1)由![]() ,则
,则![]() ,又由
,又由![]() ,得
,得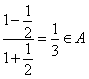 ,
,
再由![]() ,得
,得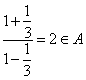 ,而
,而![]() ,得
,得![]() ,
,
故![]() 中元素为
中元素为![]() .
.
(2)
![]() 不是
不是![]() 的元素.若
的元素.若![]() ,则
,则![]() ,
,
而当![]() 时,
时,![]() 不存在,故0不是
不存在,故0不是![]() 的元素.
的元素.
取![]() ,可得
,可得![]() .
.
(3)
猜想:①![]() 中没有元素
中没有元素![]() ;
;
②![]() 中有4个,且每两个互为负倒数.
中有4个,且每两个互为负倒数.
①由上题知:![]() .若
.若![]() ,则
,则![]() 无解.故
无解.故![]()
②设![]() ,则
,则![]()
![]() ,
,
又由集合元素的互异性知,![]() 中最多只有4个元素
中最多只有4个元素![]() ,且
,且![]()
![]() .显然
.显然![]() .
.
若![]() ,则
,则![]() ,得:
,得:![]() 无实数解.
无实数解.
同理,![]() .故
.故![]() 中有4个元素.
中有4个元素.