第7课时 平均数及其估计（一）
同步导学
【学习导引】
理解平均数的定义，会用多种方法，如定义法，频数平均数法，频率平均数法，新数据法等求平均数．
【范例展示】
例1．求下列各组数据的平均数
（1）1，7，10，8，5，6，0，3，10，7；
（2）168，165，170，170，171，162，168，166，165，168．
例2．在一次中学生田径运动会上，参加男子跳高的若干名运动员的成绩如下表所示：
| 成绩（单位：米） | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 |
| 人数 | 2 | 8 | 5 | 6 | 3 |
（1）有多少名运动员参加了这次跳高比赛？
（2）求这些运动员的平均成绩（结果保留3个有效数字）．
同步测评
【自我测评】
1．为了解某商店的月营业额，在一月中抽查了5天的营业额如下（单位：元）：14845，25306，18847，11672，16330，则这个商店在该月里的平均营业额约是 （ ）
A．17400元 B．27300元 C．16000元 D．21000元
2．某人对去莫干山旅游的游客人数进行了统计：10天中，有3天每天的游客人数为400人，有2天每天的游客人数为600人，有5天每天的游客人数为350人，那么这10天中平均每天的游客人数为 （ ）
A．415人 B．425人 C．450人 D．400人
3．有8个数的平均数是11，还有12个数的平均数是12，则这20个数的平均数是 （ ）
A．11.6 B．232 C．23.2 D．11.5
4．为了让人感受丢弃塑料袋对环境造成的影响，某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量，结果如下（单位：个）：33 25 28 26 25 31 ，如果该班有45名学生，那么根据提供的数据估计本周全班同学各家总共丢弃塑料袋的数量约为 （ ）A．9000个 B．1080个 C．1260个 D．1800个
5．设样本为
，则样本平均数为
．
6．某班级进行一项素质考核，满分5分，3分（包括3分）以上合格，得1分、2分、3分、4分和5分的 人所占该班人数的比例分别为5%、10%、35%、40%和10%，试求该班的平均分．
【拓展探究】
某辆汽车从甲地以
米/秒的速度匀速行驶至乙地后，又以
米/秒的速度返回至甲地，求汽车在整个行驶过程中的平均速度．
【回顾反思】
如果将【自我测评】中的第3题变为：若
个数的平均数是
，
个数的平均数是
，则这
个数的平均数是
第8课时 平均数及其估计（二）
同步导学
【学习导引】
理解平均数的意义，会利用样本平均数估计总体平均数．
【范例展示】
例1．某班进行个人投篮比赛，受污损的下表在规定时间内投进个球的人数分布情况：
| 进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进 | 1 | 2 | 7 | 2 |
同时，已知进球3个或3个以上的人平均每人投进3.5个球；进球4个或4个以下的人平均每人投进2.5个球．问投进3个球和4个球的各有多少人？
例2．某养鱼户搞池塘养鱼已三年，头一年放养鲢鱼苗20000尾，其成活率约为70%，在秋季捕捞时，随意捞出10尾鱼，称得每尾鱼的重量如下（单位：千克）：
0.8，0.9，1.2，1.3，0.8，0.9，1.1，1.0，1.2，0.8．
（1）根据样本平均数估计这塘鱼的总产量是多少千克？
（2）如果把这塘鲢鱼全部卖掉，其市场售价为每千克4元，那么能收入多少元？除去当年的提交成本16000元，第一年纯收入多少元？
（3）已知该养鱼户这三年纯收入为132400元，求第二年、第三年平均每年的增长率是多少？
同步测评
【自我测评】
1．赵强同学解了一本书，共280页，要在两周内读完，当他读了一半时，发现如果每天要多读21页才能在借期内读完，他读前一半时，平均每天读多少页？如果设读前一半时，平均每天读页，则下面所列方程中，正确的是
（ ）
A．
B．
C．
D． 
2．有一次向“希望工程”捐款的活动中，若已知小明的捐款比他所在的学习小组中13人捐款的平均数多2元，则下列的判断中，正确的是 （ ）
A．小明在小组中捐款不可能是作多的
B．小明在小组中捐款可能排在第12位
C．小明在小组中捐款不可能比捐款排在第七位的同学少
D．小明在小组中捐款可能是最少的
3．相同质量的甲乙两金属密度为
克/
和 
克/，则这两种金属的合金密度（ ）
A．
B．
C．
D．
4．3，7，4，
四个数平均数为5，而18，9，7，
平均数为10，则
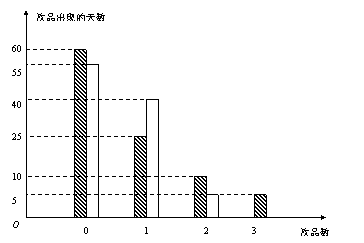5．一组数据
的平均数为
，则一组新数据
的平均数为
6．某厂对甲、乙两位优秀工人进行了为期100天的技术考核，从而升任技术最好者为工长，考核结果如图所示，问应确定谁为工长？
【拓展探究】
甲、乙两人同时在同一粮店购买粮食（假设两次购买粮食的单价不相同），甲每次购买粮食100千克，乙每次购买粮食用去100元，设甲乙两人第一次购买粮食的单价为每千克元，第二次购买粮食的单价为每千克元．
求：（1）甲乙两次购买粮食的平均单价为多少？
（2）谁两次购粮的平均单价比较低？
【回顾反思】
由【自我测评】第5题，你能得到什么规律？
第9课时 方差与标准差（一）
同步导学
【学习导引】
掌握方差、标准差的计算公式及它们的简化公式．
【范例展示】
例１．求下列数据的方差和标准差．
（１）
，
，
，
，
，；
（２）
，
，
，
，
，
，
，
，
．
例２．求数据
，
，
，
，
，
，
，
，
的标准差．
同步测评
【自我测评】
１．一组数据为
，，
，
，，则这组数据的标准差为
（ ）
A．
B．
C．
D．
２．在样本方差公式
中，下列说法不正确的是 （ ）
A．是样本容量 B．
是样本的个体 C．
是样本的平均数 D．
是样本方差
３．某中学人数相等的甲、乙两班学生参加同一次数学测验，两班平均分和方差分别为
=82分，
＝82分，
那么成绩较为整齐的是
（ ）
A．甲班 B．乙班 C．两班一样整齐 D．无法确定
4．已知一个样本的方差是
，则这个样本的平均数是
5．已知样本
的平均数是10，则样本方差等于
6．甲乙两人数学成绩的茎叶图如图所示
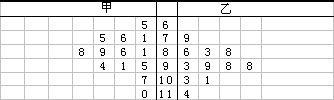
（１）求出这两名同学的数学成绩的平均数、标准差；
（２）比较两名同学的成绩，谈谈你的看法．
【拓展探究】
一组数据
，其中是小于10的自然数，且数据的方差是整数，求数据的标准差？
【回顾反思】
在【自我测评】第2题中是样本方差的简化公式，你还能写出其它公式么？
第10课时 方差与标准差（二）
同步导学
【学习导引】
理解方差标准差的意义，掌握用样本方差或标准差去估计总体方差或总体标准差的方法．
【范例展示】
例１．从甲乙两种玉米苗中各抽10株，分别测得它们的株高如下（单位：
）
甲：25 41 40 37 22 14 19 39 21 42
乙：27 16 44 27 44 16 40 40 16 40
试评定哪种玉米长的高，哪种长的整齐？
例２．设一组数据，其标准差为
，另一组数据
，其标准差为
，求和的关系式．
同步测评
【自我测评】
1．甲乙两中学生在一年里各学科平均分相等，但他们的方差不相等，正确评价他们的学习情况是 （ ）
A．因为他们的平均分相等，所以学习水平一样
B．成绩虽然一样，方差较大的，说明潜力大，学习态度踏实
C．表面上看这两个中学生平均成绩一样，但方差小的学习成绩稳定
D．平均分相等，方差不等，说明学习水平不一样，方差较小的同学成绩不稳定，忽高忽低
2．一组数据的方差是２，将这组数据扩大为原来的2倍，则所得新的一组数据的方差是（ ）
A．2 B．4 C．8 D．16
3．已知一组数据
的平均数是2，方差是
，那么另一组数据
的平均数和方差分别是
（ ）
A．2，
B．2，1
C．4，
D．4，3
4．某班5次数学测试中，甲乙两同学的成绩如下：（单位：分）
甲：90 92 88 92 88 乙：94 86 88 90 92
则甲乙两人成绩相比较得出结论是 稳定．
5．数据
的平均数为
，其中是方程
的两个根，则这组数据的方差是 ．
6．从甲乙两位车工加工的零件中，各抽查了8件，量得直径尺寸如下（单位：毫米）
甲：35.01，35.03，35.05，34.98，34.96，35.00，35.02，34.95
乙：35.04，34.99，34.97，35.00，35.03，35.01，34.99，35.01
求（１）和；（２）
和
；（３）说明谁的零件尺寸更接近于35毫米？
【拓展探究】
已知一个样本
，其中为实数，且满足
，则这个样本的标准差为
【回顾反思】
由【范例展示】例2，你能总结方差的运算性质么？
第11课时 线性回归方程（一）
同步导学
【学习导引】
会判断变量之间是否有相关关系，会画散点图，并会利用最小平方法求解回归直线．
【范例展示】
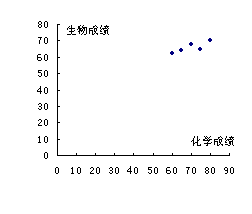
例1．5个学生的化学和生物成绩如下表：
|
生物 | A | B | C | D | E |
| 化学 | 80 | 75 | 70 | 65 | 60 |
| 生物 | 70 | 65 | 68 | 64 | 62 |
学生画出散点图，并判断它们是否有相关关系．
例2．已知10只狗的血球体积及红血球数的测量值如下表：
|
| 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
|
| 6.35 | 6.30 | 9.52 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 8.72 |
（1）画出上表的散点图；
（2）求出回归直线并画出图形．
同步测评
【自我测评】
1．下列两个变量之间的关系，哪个不是函数关系 （ ）
A．角度和它的正弦值 B．圆的半径和它的面积
C．人的年龄和他的体重
D．凸边形的边数与它的内角和
2．设有一个回归直线方程
，则变量增加一个单位时，平均 （ ）
A．增加1.5个单位 B．增加2单位 C．减少1.5单位 D．减少2单位
3．线性回归方程
必定过点
（ ）
A．
B．
C．
D．
4．回归方程的系数
的最小二乘法估计使函数
最小，
函数指 （ ）
A．
B．
C．
D． 
5．以下有关线形回归的说法中，
（1）相关关系的两个变量不是因果关系；
（2）散点图能直观地反映数据的相关程度；
（3）回归直线最能代表线形相关的两个变量之间的关系；
（4）任一组数据都有回归方程．
正确的有
6．观察两相关变量得如下数据：
|
| －1 | －2 | －3 | －4 | －5 | 5 | 3 | 4 | 2 | 1 |
|
| －9 | －7 | －5 | －3 | －1 | 1 | 5 | 3 | 7 | 9 |
求两变量间的回归方程？
【拓展探究】
【回顾反思】
由【自我测评】第1题，你能说出相关关系和函数关系的区别和联系么？
第12课时 线性回归方程（二）
同步导学
【学习导引】
会运用线形回归的方法定量分析两个变量之间的线形关系．
【范例展示】
例1．某医院用光电比色计检验尿汞时，得尿汞含量
与消光系数如下表：
| 尿汞含量 | 2 | 4 | 6 | 8 | 10 |
| 消光系数 | 64 | 138 | 205 | 285 | 360 |
（1）用统计方法判断尿汞含量与消光系数是否相关？（2）求出回归直线方程．（3）能预测尿汞含量为
时的消光系数吗？
例2．一机器可以按各种不通速度运转，其生产的物件有一些会有问题，每小时生产有问题物件的多少，随机器运转的速度而变化，下列即为其试验结果：
速度（转/秒） 8 12 14 16
每小时生产有问题物件数 5 8 9 11
（1）求出机器速度的影响每小时生产有问题物件数的回归直线方程；
（2）若实际生产中所允许的每小时最大问题物件数为10，那么，机器的速度不得超过多少转/秒？
同步测评
【自我测评】
1．工人工资（元）依劳动生产率（千元）变化的回归方程为
，下列正确的是（ ）
A．劳动生产率为1000元时，工资为130元 B．劳动生产率提高1000元时，工资为80元
C．劳动生产率提高1000元时，工资为130元D．当月工资250元时，劳动生产率为2000元
2．对于线性相关系数
，叙述正确的是
（ ）
A．
越大，相关程度越大，反之，相关程度越小
B．
越大，相关程度越大，反之，相关程度越小
C．
且
越接近于1，相关程度越大，越接近于0，相关程度越小
D．以上说法都不对
3．为了考察两个变量
之间的线形相关性，甲乙两个同学各自独立的作10次和15次，并且利用线形回归方法，求得回归直线分别为
，已知在两个人的试验中发现对变量的观测数据的平均值恰好相等，都为，对变量的观测数据的平均值也恰好相等，都为
，那么下列说法正确的是
（ ）
A．直线有交点为
B．直线相交，但是交点未必为
C．直线 斜率相等，所以必定平行 D．直线必定重合
4．对于数据
线形回归方程
中的
，
|
| 100 | 120 | 140 | 160 | 180 |
|
| 45 | 54 | 62 | 75 | 92 |
5．已知两个变量之间有线形
相关性，5次试验的观测数据如右表：
那么变量关于的回归方程为
6．以下是某地收集到的新房屋的销售价格和房屋的面积的数据：
房屋面积（
） 115 110 80 135 105
销售价格（万元） 24.8 21.6 18.4 29.2 22
（1）画出数据对应的散点图；（2）求线性回归方程，并在散点图中加上回归直线；(3)据（2）的结果估计当房屋面积为150时的销售价格．
【拓展探究】
证明恒等式：
，其中
，从而回归直线的斜率还可以写成
．
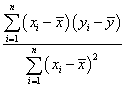【回顾反思】
你能总结求线形回归方程的一般步骤么？
本章测评
一、选择题
1．（1）教育局督学组到学校检查工作，临时需在每个班各抽调二人参加座谈；（2）某班期中考试有
人在
分以上，
人在
分，
人不及格，现欲从中抽出
人研讨进一步改进教和学；（3）某班元旦聚会，要产生两名“幸运者”．对这三件事，合适的抽样方法分别为 （
）
A．分层抽样，分层抽样，简单随机抽样
B．系统抽样，系统抽样，简单随机抽样
C．分层抽样，简单随机抽样，简单随机抽样
D．系统抽样，分层抽样，简单随机抽样
2．下列关于茎叶图的叙述正确的是 （ ）
A． 将数组的数按位数进行比较，将数大小基本不变或变化不大的位作为一个茎，将变化大的位的数作为叶，列在茎的后面
B． 茎叶图只可以分析单组数据，不能对两组数据进行比较
C． 茎叶图更不能表示三位数以上的数据
D．画图时茎要按照从小到的顺序从下向上列出，其茎的叶可随意同行列出
3．在抽查某产品的尺寸过程中，将其尺寸分成若干组，
是其中一组，抽查出的个体数在该组上的频率为，该组上的直方图的高为
，则
等于
（ ）
A．
B．
C．
D．与
无关
4．由一组样本数据
得到的回归直线方程，那么下面说法不正确的是
（ ）
A．直线必经过点
B．直线至少经过点中的一个
C．直线的斜率为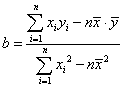
D．直线方程和各点的总离差
是该坐标平面上所有直线与这些点的离差中最小的直线。
二、填空题
５．把某校的一次数学考试成绩作为样本，样本数据落在
之间的频率是
，则可估计，这个学校里的数学成绩在之间的学生约占___________．
６．把容量为的某个样本数据分为
组，并填写频率分布表，若前七名的累积频率为
，而剩下三组的频数成公比大于的整数等比数列，则剩下三组的频数最高的一组的频数为________．
７．是
的平均数，是
的平均数，是
的平均数，则，，的之间关系是__________．
８．某超市“五
一”过后统计了最近6个月某种鲜牛奶的进价和售价（单位：元）的对应数据，如下表：
|
| 3 | 5 | 2 | 8 | 9 | 12 |
|
| 4 | 6 | 3 | 9 | 12 | 14 |
则回归直线方程为 ．
三、解答题
９．为制定本市初中七、八、九年级学生校服的生产计划，有关部门准备对
名初中男生的身高作调查，现有三种调查方案：
．测量少体校中名男子篮球、排球队员的身高；
．查阅有关外地名男生身高的统计资料；
．在本市的市区和郊县各任选一所完全中学、两所初级中学，在这六所学校有关的年级（１）班中，用抽签的方法分别选出名男生，然后测量他们身高．
为了达到估计本市初中这三个年级男生身高分布的目的，你认为采用上述哪一种调查方案比较合理，为什么？
１０．已知
个数据的分组以及各组的频数如下：
1－3、2 9－11、9 3－5、3 11－13、5 5－7、6 13－15、3 7－9、10 15－17、2
列出这组数据的频率分布表，并画出频率分布直方图．
１１．某校高三学生甲、乙两人在
月份～
月份进行的次模拟考试中，成绩如下：（单位：分）
甲：
乙：
绘出甲、乙两名学生模拟考试成绩折线图，说明甲、乙两名学生谁的潜力大．
１２．要分析学生初中升学的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽选名学生，分析他们入学的数学成绩（）和高一年级期末数学考试成绩（）（如下表）：
| 编号 | １ | ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | １０ |
|
| ６３ | ６７ | ４５ | ８８ | ８１ | ７１ | ５２ | ９９ | ５８ | ７６ |
|
| ６５ | ７８ | ５２ | ８２ | ９２ | ８９ | ７３ | ９８ | ５６ | ７５ |
（１） 画出散点图；
（２）
对变量和进行相关性检验，如果和之间具有线性相关关系，求出一元线性回归方程；
（３）
若某学生入学数学成绩为
分，试估计他高一年级期末数学考试成绩．
第7课时
【范例展示】
例1、分析：（1）用平均数公式求解；（2）数值较大，可考虑新数据法
解答：（1）
（2）
评析：我们在计算平均数时，选择恰当的方法，可以使得计算简单．
例2、分析：（1）将各成绩段人数相加即可；（2）用频数平均数公式计算平均成绩．
解答：（1）
共有24名运动员参加比赛．
（2）
（米）．
所以这些运动员的平均成绩为1.60米．
评析：本题也可以用新数据法计算其平均成绩．在用平均数公式解决实际问题时，要灵活选择恰当的平均数计算方法，这样才能使计算简便．
【自我测评】
1、C 2、D 3、A 4、C 5、
6、解答：班级平均得分
分．
答：该班平均得分3.4分．
【拓展探究】
解答：设甲地到乙地路程为，则根据题意，得
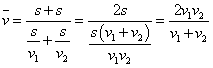（米/秒）
【回顾反思】
第8课时
【范例展示】
例1、分析：利用方程的思想，设立未知数，用平均数公式列方程组求解．
解答：设投进3个球的人数为，投进4个球的人数为，则由平均数的意义，可得
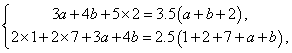即
解得
答：投进3个球的人数为9人，投进4个球的人数为3人．
评析：本题实质上考查平均数的概念及计算公式，应用平均数公式得到关系式，转化为方程组问题求解．
例2、分析：首先应计算出样本的平均数，然后用样本的平均数去估计总体的平均数，从而计算出总产量、总收入，进而求出纯收入．
解答：（1）
＝
（千克），
（千克）．
（2）
（元），56000
16000=40000（元）．
（3）设平均每年的增长率为，根据题意得，
，解得
（舍去），
所以增长率为10%．
评析：由于鱼在池塘中，无法精确计算其重量，只有用样本平均数去估计总体平均数，再由成活率，则可以估计池塘中的鱼的总量．
【自我测评】
1、C 2、B 3、D 4、10 5、
6、解答：
件，
件，由于工人乙平均每天出次品0.5件，低于甲，所以按题意要求应确定乙升任工长．
【拓展探究】
解答：（1）根据题意，甲两次购粮分别用去
元、
元，乙两次购粮的数量为
（千克）和
（千克），所以甲两次购粮的平均单价为
，乙两次购粮的平均单价为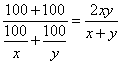
．
（2）
，又
，
，
．
又由已知
，
．
， 
．
答：乙两次购粮的平均单价比较低．
【回顾反思】
一组数据的平均数为，则一组新数据
的平均数为
第9课时
【范例展示】
例1、解答：（１）
，
．
（２）方法一，用简化公式：
取
，则有
，
．
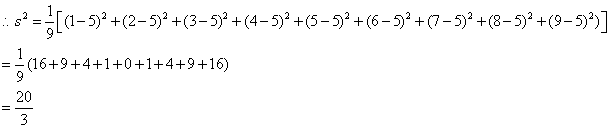方法二，用新数据法：取，则有，
例2、解答：取
，取得新数据：，，，，５，
，，，
．
，
，
．
【自我测评】
1、A 2、D 3、B 4、2 5、0.065
6、解答：（１）＝87，
＝12.7，＝95，
＝9.7
（２）由＝87<＝95，且＝12.7>＝9.7，故甲的数学学习状况不如乙的数学学习状况．
【拓展探究】
解答：
又
且
均为整数，
或5．
当
时，
，所以
；当
时，
，所以
．
【回顾反思】
新数据法：
等。
第10课时
【范例展示】
例1、分析：要知道哪种玉米的苗长的高，只要比较甲、乙两种玉米的平均高度即可；要知道哪种玉米的苗长的整齐，只要比较两种玉米苗高的方差大小就可以得到结论．
解答：（１）
，
，
．
（２）
，所以乙种玉米的苗长的高；甲种玉米的苗长得整齐．
评析：比较两组数据平均水平的高低，只需要计算它们的平均数，并比较它们的大小即可，同样，要看两组数据的波动性，只需要计算出它们的方差或标准差，并比较它们的大小即可，但需要注意的是，平均数越大数据平均水平越高；方差或标准差越大，数据的波动越大、稳定性约差．
例2、分析：对照标准差基本公式，先把这两组数据的平均数代数式表示出来，再运用标准差基本公式化简可得和的关系式．
解答：设数据的平均数为，即
，设的平均数为
，即
，
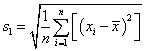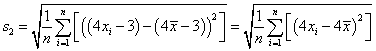
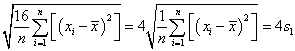所以
，
=
，所以
．
评析：由本例类似可得如下结论：若把一组数据的每一个数扩大
倍并加上一个常数，则它的标准差扩大倍，而于常数无关．
【自我测评】
1、C 2、C 3、D 4、甲 5、2
6、解答：
（１）
毫米，
毫米
（２）
毫米2
（３）因为，>，所以乙的零件的尺寸更接近于35毫米．
【拓展探究】
解答：
【回顾反思】
解答：如果一组数据的方差为
，则
（1）新数据
的方差仍为
（2）新数据
的方差为
（3）新数据
的方差为
第11课时
【范例展示】
例1、分析：涉及两个变量：化学成绩与生物成绩，可以以化学成绩为自变量，考察因变量生物成绩的变化趋势．
解答：以轴表示化学成绩，轴表示生物成绩，可得相应的散点图如图所示：
由散点图可见，两者之间具有相关关系．
反思：判断变量间有无相关关系，一种常用的简便可行的方法就是绘制散点图
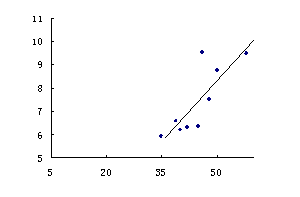
例2、分析：画散点图时，横轴和纵轴的长度单位可以不一致．
解答：（1）如图所示
（2）
设回归直线的方程为
，则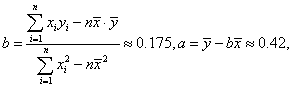
回归直线的方程为
，回归直线的图形如上图．
评析：由于横纵轴长度单位不一致，回归直线在图形中的形成和实际情况是不同的．
【自我测评】
1、C 2、C 3、D 4、A 5、（1）（2）（3）
6、解答：列表：
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| －1 | －2 | －3 | －4 | －5 | 5 | 3 | 4 | 2 | 1 |
|
| －9 | －7 | －5 | －3 | －1 | 1 | 5 | 3 | 7 | 9 |
|
| 9 | 14 | 15 | 12 | 5 | 5 | 15 | 2 | 14 | 9 |
计算得：
，
，
，
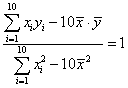，所以，回归直线方程为
．
【拓展探究】
【回顾反思】
解答：相同点：两者均是指两个变量之间的关系；
不同点：函数关系是一种确定关系，是两个非随机变量的关系，而相关关系是非随机变量与随机变量的关系；函数关系是一种因果关系，而相关关系不一定是因果关系，也可能是伴随关系。
第12课时
【范例展示】
例1、分析：由题意需作回归分析、先画出其散点图，看其是否呈直线形，然后求出回归直线方程．
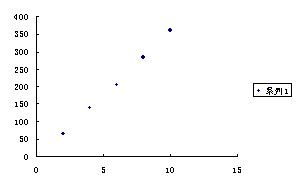解答：（1）画出其散点图，观察散点图，可以发现5个样本点都落在一条直线附近，所以变量属于线性相关．
（2）由于尿汞含量与消光系数线性相关，可利用公式求得
．
（3）当时，
，可知尿汞含量为时的消光系数为173．
例2、分析：把题中的量用回归分析的专用术语改写后在顺着回归分析的一般步骤解题．
解答：（1）用来表示机器速度，表示每小时生产有问题的物件数，那么4个样本数据为：
，则
所以，回归直线的斜率为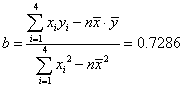
，
，
所以回归直线方程为
（2）由
，
，所以机器的速度不能超过14.9013转/秒．
评析：我们在求经验公式后，往往用来做为现实生产中两变量之间相关关系的近似关系，从而可以用来指导生产实践．
【自我测评】
1、B 2、C 3、A 4、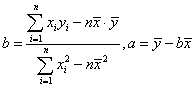
5、
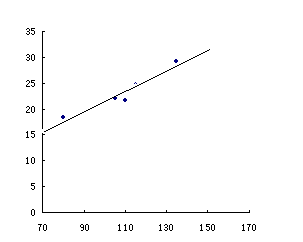6、解答：（1）如图所示
（2）
，
所以回归直线方程为
．
（3）由（2），当
时，为31.2466万元．
【拓展探究】
证明：
．
上式中令
则有恒等式：
所以得证．
【回顾反思】
求线形回归直线方程的操作步骤是：
第一步：列表
；第二步：计算：
；
第三步：代入公式计算
的值；第四步：写出回归方程。
本章测试
一、选择题
1、D 2、A 3、C 4、B
二、填空题
5、35% 6、16 7、
8、
三、解答题
9、解答：A中，少体校的男子篮球、排球的运动员的身高一定高于一般的情况，因此无法用测量的结果去估计总体的结果；B中，用外地学生的身高也不能准确地反映本地学生身高的实际情况；而C中的抽样方法符合随机抽样，因此用C方案比较合理。
10、解答：
频率分布表：
| 分组 | 频数 | 频率 |
| 1－3 | 2 | 0.050 |
| 3－5 | 3 | 0.075 |
| 5－7 | 6 | 0.150 |
| 7－9 | 10 | 0.250 |
| 9－11 | 9 | 0.225 |
| 11－13 | 5 | 0.125 |
| 13－15 | 3 | 0.075 |
| 15－17 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
频率分布直方图略
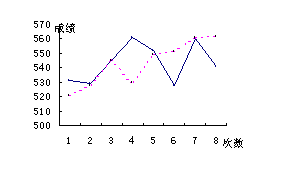11、解答：
 |
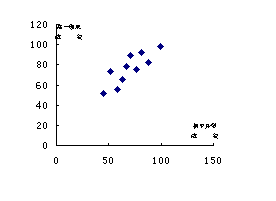由折线图可以看出，乙的潜力大
12、解答：（1）从入学成绩
与
高一期末考试成绩
两组变量
的散点图来看，这两组变量具有
线性关系；
（2）因为
，
，
，
，
所以线性回归直线方程为
（3）若某学生入学数学成绩为80分，代入上式得
分，即这个学生高一期末数学成绩预测值为84分。