高一数学第一学期模块验收试卷
数学必修2
| 得分 | 评卷人 |
一、选择题 :(本大题共10小题 ,每小题4分,共40分,在每小题给出的四个选择项中,只有一项是符合题目要求的. 请将选择题答案填入下答题栏内)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
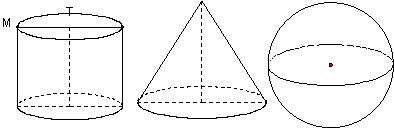
|
|
1.若直线![]() 经过原点和点A(-2,-2),则它的斜率为( )
经过原点和点A(-2,-2),则它的斜率为( )
A.-1 B.1 C.1或-1 D.0
2.各棱长均为![]() 的三棱锥的表面积为( )
的三棱锥的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
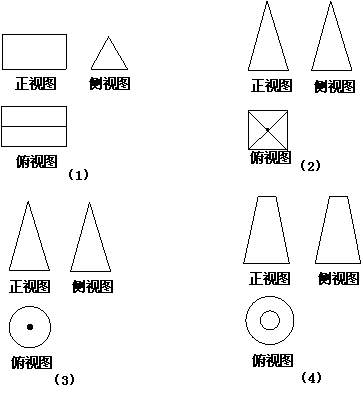 3. 如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
3. 如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
A.三棱台、三棱柱、圆锥、圆台 B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台 D.三棱柱、三棱台、圆锥、圆台
4.经过两点(3,9)、(-1,1)的直线在x轴上的截距为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
5.已知A(1,0,2),B(1,![]() 1),点M在
1),点M在![]() 轴上且到A、B两点的距离相等,则M点坐标为( )
轴上且到A、B两点的距离相等,则M点坐标为( )
A.(![]() ,0,0) B.(0,
,0,0) B.(0,![]() ,0) C.(0,0,
,0) C.(0,0,![]() ) D.(0,0,3)
) D.(0,0,3)
6.如果AC<0,BC<0,那么直线Ax+By+C=0不通过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知圆心为C(6,5),且过点B(3,6)的圆的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.在右图的正方体中,M、N分别为棱BC和棱CC1的中点,
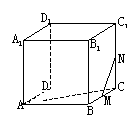 则异面直线AC和MN所成的角为( )
则异面直线AC和MN所成的角为( )
A.30° B.45°
C.90° D. 60°
9.给出下列命题
①过平面外一点有且仅有一个平面与已知平面垂直
②过直线外一点有且仅有一个平面与已知直线平行
③过直线外一点有且仅有一条直线与已知直线垂直
④过平面外一点有且仅有一条直线与已知平面垂直
其中正确命题的个数为( )
A.0个 B.1个 C.2个 D.3个
10.点![]() 在圆
在圆![]() 内,则直线
内,则直线![]() 和已知圆的公共点的个数为( )
和已知圆的公共点的个数为( )
A.0 B.1 C.2 D.不能确定
二、填空题(每题4分,共20分)
11.已知原点O(0,0),则点O到直线x+y+2=0的距离等于 .
12.经过两圆![]() 和
和![]() 的交点的直线方程
的交点的直线方程
13.过点(1,2),且在两坐标轴上截距相等的直线方程
14.一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为 .
 |
15.已知两条不同直线![]() 、
、![]() ,两个不同平面
,两个不同平面![]() 、
、![]() ,给出下列命题:
,给出下列命题:
①若![]() 垂直于
垂直于![]() 内的两条相交直线,则
内的两条相交直线,则![]() ⊥
⊥![]() ;
;
②若![]() ∥
∥![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;
内的所有直线;
③若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ;
;
④若![]()
![]()
![]() ,
,![]() ,则
,则![]() ⊥
⊥![]() ;
;
⑤若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
三、解答题(5道题,共40分)
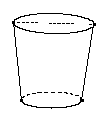
16.(本大题6分)如图是一个圆台形的纸篓(有底无盖),它的母线长为50cm,两底面直径分别为40 cm和30 cm;现有制作这种纸篓的塑料制品50m2,问最多可以做这种纸篓多少个?



 17.(本大题8分)求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
17.(本大题8分)求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
18.(本大题8分)求圆心在![]() 上,与
上,与![]() 轴相切,且被直线
轴相切,且被直线![]() 截得弦长为
截得弦长为![]() 的圆的方程.
的圆的方程.
19.(本大题8分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线![]() C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
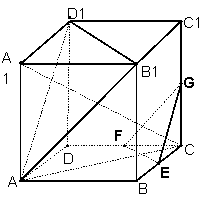 (2)求证:平面A B1D1∥平面EFG;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .
20.(本大题10分)已知方程![]() .
.
(1)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(2)若(1)中的圆与直线![]() 相交于M,N两点,且OM
相交于M,N两点,且OM![]() ON(O为坐标原点)求
ON(O为坐标原点)求![]() 的值;
的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.
数学必修2参考答案
一、选择题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | D | C | A | C | C | A | D | B | A |
二、填空题:
11.![]() 12.
4 x+3y+13=0 13.
12.
4 x+3y+13=0 13.![]() 14.3:1:2.15.
①④
14.3:1:2.15.
①④
三、 解答题:
16.解:![]() -----------1分
-----------1分
=![]()
![]() =0.1975
=0.1975![]() ----------3分
----------3分
![]() 80(个)-------5分
80(个)-------5分
答:(略)--------6分
17.解:![]() 解得
解得![]() --------2分
--------2分
所以交点(-1,2)
(1)![]() -----3分
-----3分
直线方程为![]() --------5分
--------5分
(2)![]() ---------6分
---------6分
直线方程为![]() --------8分
--------8分
18.解:由已知设圆心为(![]() )--------1分
)--------1分
与![]() 轴相切则
轴相切则![]() ---------2分
---------2分
圆心到直线的距离![]() ----------3分
----------3分
弦长为![]() 得:
得:![]() -------4分
-------4分
解得![]() ---------5分
---------5分
圆心为(1,3)或(-1,-3),![]() -----------6分
-----------6分
圆的方程为![]() ---------7分
---------7分
或![]() ----------8分
----------8分
19.解:(1)∵![]()
![]() 平面ABCD=C,在正方体ABCD-A1B1C1D1
平面ABCD=C,在正方体ABCD-A1B1C1D1
![]() 平面ABCD
平面ABCD
∴AC为![]() 在平面ABCD的射影
在平面ABCD的射影
∴![]() 为
为![]() 与平面ABCD所成角……….1分
与平面ABCD所成角……….1分
正方体的棱长为![]()
∴AC=![]() ,
,![]() =
=![]()
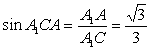
………..2分
(2)在正方体ABCD-A1B1C1D1
连接BD,![]() ∥
∥![]() ,
,![]() =
=![]()
![]()
![]() 为平行四边形
为平行四边形
∴![]() ∥
∥![]()
∵E,F分别为BC,CD的中点
∴EF∥BD
∴EF∥![]() …………3分
…………3分
∵EF![]() 平面GEF,
平面GEF,![]()
![]() 平面GEF
平面GEF
∴![]() ∥平面GEF
…………4分
∥平面GEF
…………4分
同理![]() ∥平面GEF
∥平面GEF
∵![]()
![]()
![]() =
=![]()
∴平面A B1D1∥平面EFG ……………5分
(3)在正方体ABCD-A1B1C1D1
∴![]() 平面ABCD
平面ABCD
∵EF![]() 平面ABCD
平面ABCD
∴![]() EF
…………6分
EF
…………6分
∵ABCD为正方形
∴AC![]() BD
BD
∵EF∥BD
∴AC![]() EF
………..7分
EF
………..7分
![]()
∴EF![]() 平面AA1C
平面AA1C
∵EF![]() 平面EFG
平面EFG
∴平面AA1C⊥面EFG …………….8分
20.解:(1)![]()
D=-2,E=-4,F=![]()
![]() =20-
=20-![]()
![]()
![]() …………2分
…………2分
(2)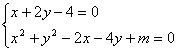
![]() 代入得
代入得
![]() ………..3分
………..3分
![]() ,
,![]() ……………4分
……………4分
∵OM![]() ON
ON
得出:![]() ……………5分
……………5分
∴![]()
∴![]() …………….7分
…………….7分
(3)设圆心为![]()
![]() …………….8分
…………….8分
半径![]() …………9分
…………9分
圆的方程![]() ……………10分
……………10分