|
高一数学第一学期统一测试(二)
高一数学
一、选择题(每小题有且只有一个答案正确,每小题5分,共60分)
1.下列结果是![]() 的是
( )
的是
( )
A.![]() -
-![]() +
+![]() B.
B.![]() -
-![]() +
+![]()
C.![]() -
-![]() +
+![]() D.
D.![]() -
-![]() +
+![]()
2.已知MP、OM、AT分别为![]() (
(![]() )的正弦线、余弦线、正切线,则一定有( )
)的正弦线、余弦线、正切线,则一定有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3. 已知![]() ,角
,角![]() 的终边经过点P(-3
的终边经过点P(-3![]() ,4
,4![]() ),那么
),那么![]() 的值等于
( )
的值等于
( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
4.设集合![]() 则从集合A到集合B的映射f只可能是
( )
则从集合A到集合B的映射f只可能是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设△ABC的重心为M,BC、CA、AB的中点是D、E、F,则![]() +
+![]() -
-![]() 等于 ( )
等于 ( )
A. 4![]() B. 3
B. 3![]() C. -4
C. -4![]() D.
D. ![]()
6. 同时具有性质“⑴ 最小正周期是![]() ;⑵ 图象关于直线
;⑵ 图象关于直线![]() 对称;⑶ 在
对称;⑶ 在![]() 上是增函数”的一个函数是
( )
上是增函数”的一个函数是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知![]() 为第二象限角,则下列四个值中,一定大于0的是
( )
为第二象限角,则下列四个值中,一定大于0的是
( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.实数![]() 满足
满足![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.3 C.4 D.与
B.3 C.4 D.与![]() 有关
有关
10.要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上所有的点的
的图象上所有的点的
A.横坐标伸长到原来的2倍,再向左平行移动![]() 个单位长度
( )
个单位长度
( )
B.横坐标伸长到原来的2倍,再向右平行移动![]() 个单位长度
个单位长度
C.横坐标缩短到原来的![]() 倍,再向右平行移动
倍,再向右平行移动![]() 个单位长度
个单位长度
D.横坐标缩短到原来的![]() 倍, 再向左平行移动
倍, 再向左平行移动![]() 个单位长度
个单位长度
11.已知函数![]() ,则
( )
,则
( )
A.![]() 与
与![]() 都是奇函数
B.
都是奇函数
B.![]() 与
与![]() 都是偶函数
都是偶函数
C.![]() 是奇函数,
是奇函数,![]() 是偶函数 D.
是偶函数 D.![]() 是偶函数,
是偶函数,![]() 是奇函数
是奇函数
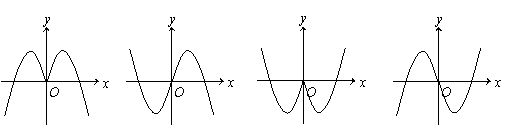 12.函数
12.函数![]() 的部分图象是
( )
的部分图象是
( )
A. B. C. D.
二、填空题:(每小题5分,共20分)
 13.函数
13.函数![]() 的定义域为________________.
的定义域为________________.
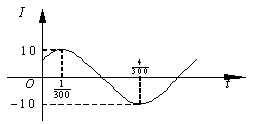
14.电流强度I(安培)随时间t(秒)变化的函数
I = Asin(wt+j)![]() 的图象如图所示,
的图象如图所示,
则当t = ![]() (秒)时的电流强度为_______.
(秒)时的电流强度为_______.
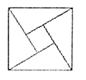 15.2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为
15.2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() =____________
=____________
16.
在函数①y=|tanx|,②y=|sin(x+![]() )|,③y=|sin2x|,④y=sin(2x-
)|,③y=|sin2x|,④y=sin(2x-![]() )四个函数中,既是以
)四个函数中,既是以![]() 为周期的偶函数,又是区间(0,
为周期的偶函数,又是区间(0,![]() )上的增函数的为:___________(写出序号)
)上的增函数的为:___________(写出序号)
三、解答题(解答应写出文字说明、证明过程或演算步骤.共70分)
17. 已知![]() ,求下列各式的值。
,求下列各式的值。
(1)![]() (2)
(2)![]()
18. 已知α为第三象限角,且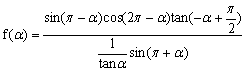
(1)化简f(α);
(2)若cos(α-)=,求f(α)的值;
(3)若α=-1860°,求f(α)的值.
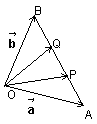
19.设点P、Q分别是线段AB的三等分点,若![]() ,
,![]() 。
。
(1)试用![]() 表示向量
表示向量![]() ,
,![]() ;
;
(2)如果点![]() 是AB的n(
是AB的n(![]() )等分点,试用
)等分点,试用![]() 表示:
表示:![]() 。(注:
。(注:![]() …
…![]() )
)
20.已知某海滨浴场海浪的高度y米是时间t(![]() ,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据:
,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据:
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
经过长期观测y=f(t)的曲线可近似地看成是函数y=Acos![]() t+b
t+b
(1)根据以上数据求函数y的最小正周期T,振幅A及解析式
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
21、已知函数![]() ,
,
(1)若![]() 有实数解,求a 的取值范围;
有实数解,求a 的取值范围;
(2)若![]() 对一切
对一切![]() 恒成立,求a的取值范围。
恒成立,求a的取值范围。
22.已知函数![]()
![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在
在![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求实数
,求实数![]() 与
与![]() 的值
的值