高一数学第二学期第一次月考试卷
班级_________. 学号_________. 姓名__________________.
一、选择题（每小题4分，共40分）
1．若
且
，则下列不等式中一定成立的是（
）
A．
B．
C．
D．
2．已知数列
，
,
…
，…，则
是这个数列的（ ）
A．第10项 B．第11项 C．第12项 D．第21项
3．在△ABC中，若
，则∠C=（ ）
A． 60° B. 90° C. 120° D．150°
4．设集合
（ ）
A．
B．
C．
D．
5．已知-9，
，-1四个数成等差数列，-9,
，-1成等比数列,则
=( )
A. -8
B . 8
C. . ±8
D . 
6．不等式
对一切
R恒成立，则实数a的取值范围是（ ）
A. 
B. 
C. 
D. 
7. 在△ABC中，∠A=60°,a=
,b=4,满足条件的△ABC（ ）
A. 无解 B. 有解 C . 有两解 D . 不能确定
8．设｛an｝是由正数组成的等比数列,且
=81,
的值是 （ ）
A . 5 B . 10 C. 20 D .2或4
9．下列结论正确的是（ ）
A.当x>0且x≠1时，
≥2
B.当x>0时，
+
≥2
C.当x≥2时，
的最小值为2
D.当0<x≤2，
无最大值
10．在等差数列{
}中，
=
，公差
，则使前n项和
取得最大值时的自然数n 的值为（ ）
A.4或5 B.5或6 C.6或7 D.不存在
二、填空题（每小题4分，共28分）
11．若不等式ax2+bx+2>0的解集为{x-
},则a+b=_________.
12．若
的三个角
，则A、B、C分别所对边
=_________.
13．在等差数列{an}中，若a4＋a6＋a8＋a10＋a12＝120，则
=
14．在△ABC中, 
则a=
15．
......
____________
16．若对于一切正实数
不等式
恒成立，则实数
的取值范围
17．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：
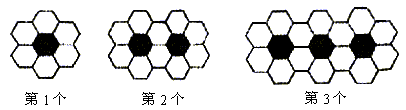
则第n个图案中有白色地面砖 块.
三、解答题：(本大题共5小题，共52分，解答应写出文字说明、证明过程或演算步骤)
（Ⅰ）求 
的值
（II）若分别是等比数列
的第1项和第2项，求数列的通项公式
19．（10分）△ABC中，内角A，B，C的对边分别为 ，b，c，tan C =
（Ⅰ）求cos C的值
（II）若
20．（10分）已知
，
（I）当
时，解不等式
；
（II）若
，解关于x的不等式。
21．（10分）某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元。该公司第1年需要付出设备的维修和工人工资等费用
万元，第2年需要付出设备的维修和工人工资等费用
万元，………，第n年需要付出设备的维修和工人工资等费用的信息如下图。
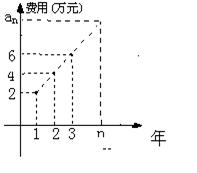（I）求
的通项公式
（II）引进这种设备后，第几年后该公司开始获利；
（III）这种设备使用多少年，该公司的年平均获利最大？
22.（12分）已知数列
的前n项和=
， n=1,2,……
（I）求数列的通项公式,
（II）记
,求数列的前n项和
余姚五中2007学年第二学期第一次月考高一数学答案及评分标准
一、选择题（每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | C | B | A | D | A | C | B | B |
二、填空题（每小题4分，共28分）
11 -14 12．1:
:2 13． 360 14．
15. 
16．a ＜ 4
17． 4n+2
三、解答题
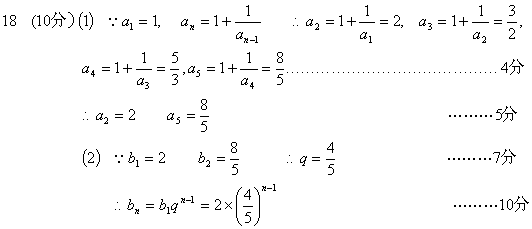
19 （10分）（I） 
tanC= 
……2分
解得
………………4分
〉0 
C是锐角
……………5分
（II）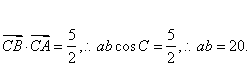
…………7分
a+b=9
C=6…10分
20 （10分）解：（I）当时，有不等式
，…………1分
∴
，
……… 2分
∴不等式的解集为： 
…………4分
（II）∵不等式
当
时，有
，∴不等式的解集为
； …………6分
当
时，有
，∴不等式的解集为
；
…………8分
当
时，不等式的解为
。
…………9分
∴ 当时，不等式的解集为；
当时，不等式的解集为；
当时，不等式的解为。
…………10分
21 （10）解：（1）由题意知，每年的费用是以2为首项，2为公差的等差数列，求得：
…………2分
（2）设纯收入与年数n的关系为f(n),则：
…………4分
由f(n)>0得n2-20n+25<0 解得
…………6分
又因为n
,n所以n=2,3,4,……18.即从第2年该公司开始获利 ………7分
（3）年平均收入为
=20-
………9分
当且仅当n=5时，年平均收益最大.所以这种设备使用5年，该公司年平均获利最大。…10
