高一下学期期末复习练习
等差数列
[重点]
等差数列的概念、等差数列的通项公式、等差数列的前n项和公式。
1．定义：数列{an}若满足an+1-an=d(d为常数)称为等差数列，d为公差。它刻划了“等差”的特点。
2．通项公式：an=a1+(n-1)d=nd+(a1-d)。若d
，表示an是n的一次函数；若d=0，表示此数列为常数列。
3．前n项和公式：Sn=
=na1+
。若d
0,表示Sn是n的二次函数，且常数项为零；若d=0，表示Sn=na1.
4．性质：①an=am+(n-m)d。② 若m+n=s+t,则am+an=as+at 。特别地；若m+n=2p,则am+an=2ap。
5.方程思想：等差数列的五个元素a1、、d、n、an、sn中最基本的元素为a1和d，数列中的其它元素都可以用这两个元素来表示。
函数思想：等差数列的通项和前n项和都可以认为是关于n的函数，因此数列问题可以借助于函数知识来解决。
[难点]
等差数列前n项和公式的推导，通项和前n项和的关系，能够化归为等差数列问题的数列的转化。如：an与sn关系：an=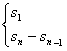
此公式适用于任何数列。
化归思想：把不熟悉的问题转化成熟悉问题的数字思想。
例题选讲
1、（福建）在等差数列｛a
｝中，已知a
=2,a
+a
=13，则a
+a
+a
等于
A.40 B.42 C.43 D.45
2、（全国）设
是公差为正数的等差数列，若
，
，则
A．
B．
C．
D．
3、已知等差数列2,5,8，……，该数列的第3k（k∈N＊）项组成的新数列｛bn｝的前4项
是 。｛bn｝的通项公式为 。
4、已知等差数列｛an｝和｛bn｝的前n项和分别为Sn 和 Tn，且
，求
＝ 。
5、已知数列｛an｝和｛bn｝满足
，求证：｛an｝为等差数列时｛bn｝必为等差数列；反之亦然。
一、选择题
1．数列{an}是首项为2，公差为3的等差数列，数列{bn}是首项为-2，公差为4的等差数列。若an=bn,则n的值为 （ ）
（A）4 （B）5 （C）6 （D）7
2．关于等差数列，有下列四个命题
（1）若有两项是有理数，则其余各项都是有理数 （2）若有两项是无理数，则其余各项都是无理数 （3）若数列{an}是等差数列，则数列{kan}也是等差数列 （4）若数列{an}是等差数列，则数列{a2n}也是等差数列
其中是真命题的个数为 （ ）
（A）1 （B）2 （C）3 （D）4
3．在等差数列{an}中,am=n,an=m,则am+n的值为 （ ）
（A）m+n （B）
（C）
（D）0
4.在等差数列{an}中，若a1+a4+a7=39,a2+a5+a8=33,则a3+a6+a9的值为 （ ）
（A）30 （B）27 （C）24 （D）21
5．一个直角三角形的三条边成等差数列，则它的最短边与最长边的比为 （ ）
（A）4∶5 （B）5∶13 （C）3∶5 （D）12∶13
6．在等差数列{an}中，Sm=Sn,则Sm+n的值为 （ ）
（A）0 （B）Sm+Sn （C）2(Sm+Sn) （D）
7．一个凸n边形内角的度数成等差数列，公差为5°，且最大角为160°，则n的值为 （ ）
（A）9 （B）12 （C）16 （D）9或16
8．在等差数列{an}中，Sp=q,Sq=q,Sp+q的值为 （ ）
（A）p+q （B）-(p+q) （C）p2-q2 （D）p2+q2
9.若数列{an}为等差数列，公差为
，且S100=145，则a2+a4……+a100的值为 （ ）
（A）60 （B）85 （C）
（D）其它值
10．若a1,a2, ……,a2n+1成等差数列，奇数项的和为75，偶数项的和为60，则该数列的项数为 （A）4 （B）5 （C）9 （D）11 （ ）
11．已知数列{an}的通项公式为an=(-1)n+1(4n-3),则它的前100项之和为 （ ）
（A）200 （B）-200 （C）400 （D）-400
12．若数列{an}由a1=2,an+1=an+2n(n
)确定，则a100的值为 （ ）
（A）9900 （B）9902 （C）9904 （D）9906
13．已知两个数列3，7，11，…，139与2，9，16，…，142，则它们所有公共项的个数为 （ ）
（A）4 （B）5 （C）6 （D）7
14．已知等差数列{an}的公差为d,d0,a1d,若这个数列的前20项的和为S20=10M，则M等于
（A）a4+a16 （B）a20+d （C）2a10+d （D）a2+2a10 （ ）
15.若关于x的方程x2-x+a=0和x2-x+b=0(a
)的四个根可以组成首项为
的等差数列，则a+b的值为 （ ）
（A）
（B）
（C）
（D）
二、填空题
1、在等差数列{an}中，已知a2+a7+a8+a9+a14=70,则a8= 。
2、在等差数列{an}中，S4=6,S8=20,则S16= 。
3、成等差数列的四个数之和为26，第一个数与第四个数积为22，则这四个数为 。
4、打一口深20米的井，打到第一米深处时需要40分钟，从第一米深处打到第二米深处需要50分钟，以后每深一米都要比前一米多10分钟，则打到最后一米深处要用 小时，打完这口井总共用 小时。
5、在项数为n的等差数列{an}中，前三项之和为12，最后三项之和为132，前n项之和为240，则n= 。
6、已知数列{an}的通项公式an=
,bn=
,则{bn}的前n项和为 。
7、数列
中 ，前n项的和为
，且满足
，则数列的通项公式为
8、已知正项数列{an}，其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列，则数列{an}的通项an＝ 。
三、解答题
1．已知数列{an}为等差数列，前30项的和为50，前50项的和为30，求前80项的和。
2．已知数列{an}的前n项和为Sn=n2+C(C为常数)，求数列{a0}的通项公式，并判断{an}是不是等差数列。
3．设等差数列{an}的前n项和为Sn,bn=
，且a3b3=，S5+S3=21,求bn。
4．已知数列{an}为首项a10，公差为d0的等差数列，求Sn=
。
5．求从1到100中所有不被3及5整除的整数之和。
6．用分期付款方式购买家用电器一件，价格为1150，购买当天先付150元，以后每月这一天都交付50元，并加付欠款的利息，月利率为1%，若交付150元以后的第一个月开始算分期付款的第一个月，问分期付款的第十个月该交付多少钱？全部贷款付清后，买这件家电实际花了多少钱？
7．已知等差数列{an},a1=29,S10=S20,问这个数列的前多少项的和最大？并求最大值。
8.已知f(x)=x2-2(n+1)x+n2+5n-7
(1)设f(x)的图像的顶点的纵坐标构成数列{an}，求证：{an}为等差数列。
(2)设f(x)的图像的顶点到x轴的距离构成{bn}，求{bn}的前n项和。
答案
第七单元 等差数列
一、选择题BBDBC AABBC BBBCD
二、填空题
1.14 2.72 3. 2,5,8,11或11,8,5,2。 4. 
。5、10，6、
7、
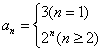8．
三、解答题
1．
S50-S30=a31+a32
+…+a50=
=30-50=-20。
∴a1+a80=-2 ∴S80=
。
2．当n=1时，a1=S1=1+c
当n
时，an=Sn-Sn-1=(n2+c)-[(n2+c)]-[(n-1)2+C]=2n-1。
∴an=
若C=0，an=2n-1,此时an-an-1=2(n){an}为等差数列。
若C0,C+11,{an}不为等差数列。
3．
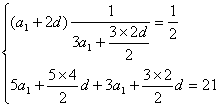
由①，得a1=d。由②，得8a1+13d=1。
故a1=d=1。
∴Sn=
4.
∴Sn=
=
。
5.设S表示从1到100的所有整数之和。S1表示从1到100中所在能被3整除的整数的和。
S2表示从1到100中所有能被5整除的整数的和。
S3表示从1到100中所有既能被3整除，又能被5整除的整数的和。
则S=
。
由99=3+（n-1）×3,得n=33。 
。
由100=5+(n-1) ×5,得n=20。 
S3表示15，30，45，…，90之和 S3=
从1到100中所有不被3及5整除的整数之和为S-S1-S2+S3=2632。
6.购买时付了150元，欠款1000元。每月付50元，分20次付完，设每月付款数顺次组成数列{an},则
a1=50+1000×0.01=60
a2=50+(1000-50) ×0.01=60-0.5
a3=50+(1000-50×2) ×0.01=60-0.5×2
类推,得
a10=60-0.5×9=55.5
an=60-0.5(n-1)(1
n20)。
∴ 付款数{an}组成等差数列，公差d=-0.5,全部贷款付清后，付款总数为
S20+150=
（元）。
7．由S20=S10得2a1+29d=0
d=-2,an=a1+(n-1)d=-2n+31
Sn==-n2+30n=-(n-15)2+225 ∴当n=15时，Sn最大，最大值为225。
8．（1）f(x)=[x-(n+1)2]+3n-8 ∴an=3n-8,∵ an+1-an=3 , ∴{an}为等差数列。
（2）b0=
当1
时，bn=8-3n,b1=5。Sn=
当n
3时。bn=3n-8 Sn=5+2+1+4+…（3n-8）
=7+
∴Sn=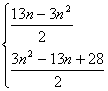
