等 差 数 列
一、选择题
1、等差数列![]() 中,
中,![]() ,那么
,那么![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2、已知等差数列![]() ,
,![]() ,那么这个数列的前
,那么这个数列的前![]() 项和
项和![]() ( )
( )
A.有最小值且是整数 B. 有最小值且是分数
C. 有最大值且是整数 D. 有最大值且是分数
3、已知等差数列![]() 的公差
的公差![]() ,
,![]() ,那么
,那么![]()
A.80 B.120 C.135 D.160.
4、已知等差数列![]() 中,
中,![]() ,那么
,那么![]()
A.390 B.195 C.180 D.120
5、从前![]() 个正偶数的和中减去前
个正偶数的和中减去前![]() 个正奇数的和,其差为( )
个正奇数的和,其差为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6、等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,前
,前![]() 项的和为
项的和为![]() ,则它的前
,则它的前![]() 项的和为( )
项的和为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7、在等差数列![]() 中,
中,![]() ,
,![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
8、一个等差数列前![]() 项和为
项和为![]() ,后
,后![]() 项和为
项和为![]() ,所有项和为
,所有项和为![]() ,则这个数列的项数为( )
,则这个数列的项数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9、已知某数列前![]() 项之和
项之和![]() 为,且前
为,且前![]() 个偶数项的和为
个偶数项的和为![]() ,则前
,则前![]() 个奇数项的和为( )
个奇数项的和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10若一个凸多边形的内角度数成等差数列,最小角为100°,最大角为140°,这个凸多边形的边比为( )
A.6 B.![]() C.10 D.12
C.10 D.12
| 一.选择题(10×5分)
|
二.填空题
1、等差数列![]() 中,若
中,若![]() ,则
,则![]() .
.
2、等差数列![]() 中,若
中,若![]() ,则公差
,则公差![]() .
.
3、在小于![]() 的正整数中,被
的正整数中,被![]() 除余
除余![]() 的数的和是
的数的和是
.
4、已知等差数列![]() 的公差是正整数,且a
的公差是正整数,且a![]() ,则前10项的和S
,则前10项的和S![]() =
=
5、一个等差数列共有10项,其中奇数项的和为![]() ,偶数项的和为15,则这个数列的第6项是
,偶数项的和为15,则这个数列的第6项是
*6、两个等差数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 和
和![]() ,若
,若![]() ,则
,则![]() .
.
三.解答题
1、
在等差数列![]() 中,
中,![]() ,
,![]() ,求
,求![]() .
.
2、设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() >
>![]() ,
,![]() <
<![]() ,
,
①求公差![]() 的取值范围;
的取值范围;
②![]() 中哪一个值最大?并说明理由.
中哪一个值最大?并说明理由.
3、己知![]() 为等差数列,
为等差数列,![]() ,若在每相邻两项之间插入三个数,使它和原数列的数构成一个新的等差数列,求:
,若在每相邻两项之间插入三个数,使它和原数列的数构成一个新的等差数列,求:
(1)原数列的第12项是新数列的第几项?
(2)新数列的第29项是原数列的第几项?
4、设等差数列![]() 的前n项的和为S n ,且S 4 =-62,
的前n项的和为S n ,且S 4 =-62,
S 6 =-75,求:
(1)![]() 的通项公式a n 及前n项的和S n ;
的通项公式a n 及前n项的和S n ;
(2)a 1 +a 2 +a 3 +……+a 14 .
5、某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元,
(Ⅰ)问第几年开始获利?
(Ⅱ)若干年后,有两种处理方案:
(1)年平均获利最大时,以26万元出售该渔船;
(2)总纯收入获利最大时,以8万元出售该渔船.
问哪种方案合算.
参考答案
一、选择题
1-5 B A C B C 6-10 C B A B A
二、填空题
1、0 2、6 3、1650 4、-10 5、3 6、6
三.解答题
1、![]() ,
,![]() .
.
2、①∵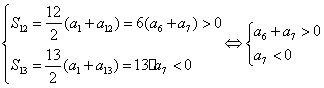 ,∴
,∴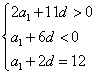
解得,![]() ,②由
,②由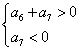
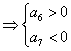 ,又∵
,又∵![]() ∴
∴![]() 是递减数列,
是递减数列,
∴![]() 中
中![]() 最大.
最大.
3、解:设新数列为
![]()
即3=2+4d,∴![]() ,∴
,∴![]()
![]() ,∴
,∴![]()
即原数列的第n项为新数列的第4n-3项.
(1)当n=12时,4n-3=4×12-3=45,故原数列的第12项为新数列的第45项;
(2)由4n-3=29,得n=8,故新数列的第29项是原数列的第8项。
4、解:设等差数列首项为a1,公差为d,依题意得![]()
解得:a1=-20,d=3。
⑴![]()
![]() ;
;
⑵![]()
![]() ∴
∴![]()
![]() .
.
5、.解:(Ⅰ)由题设知每年费用是以12为首项,4为公差的等差数列, 设纯收入与年数的关系为f(n)
∴![]() 获利即为f(n)>0
获利即为f(n)>0
∴![]()
解之得:![]() 又n∈N,∴n=3,4,…,17
又n∈N,∴n=3,4,…,17
∴当n=3时即第3年开始获利
(Ⅱ)(1)年平均收入=![]() ∵
∵![]() ≥
≥![]() ,当且仅当n=7时取“=”
,当且仅当n=7时取“=”
∴![]() ≤40-2×14=12(万元)即年平均收益,总收益为12×7+26=110万元,此时n=7 ;
≤40-2×14=12(万元)即年平均收益,总收益为12×7+26=110万元,此时n=7 ;
(2)![]() ∴当
∴当![]()
总收益为102+8=110万元,此时n=10
比较两种方案,总收益均为110万元,但第一种方案需7年,第二种方案需10年,故选择第一种。