高一下学期期末复习练习
等比数列
[重点]
等比数列的概念,等比数列的通项公式,等比数列的前n项和公式。
1.定义:数列{an}若满足![]() =q(q
=q(q![]() 为常数)称为等比数列。q为公比。
为常数)称为等比数列。q为公比。
2.通项公式:an=a1qn-1(a1![]() 0、q
0、q![]() 0)。
0)。
3.前n项和公式:Sn=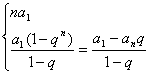 (q
(q![]() )
)
4.性质:(1)an=amqn-m。(2)若 m+n=s+t,则aman=asat,特别地,若m+n=2p,则aman=a2p,(3)记A=a1+a2+…+an,B=an+1+an+2+…a2n,C=a2n+1+a2n+2…+a3n,则A、B、C成等比数列。
5.方程思想:等比数列中的五个元素a1、q、n 、an 、Sn中,最基本的元素是a1和q,数
列中的其它元素都可以用这两个元素来表示。
函数思想:等比数列的通项和前n次和都可以认为是关于n的函数。
[难点]
等比数列前n项和公式的推导,化归思想的应用。
例题选讲
1.(湖北)若互不相等的实数![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]() ,则
,则![]() ( ) A.4 B.2 C.-2 D.-4
( ) A.4 B.2 C.-2 D.-4
2.(辽宁)(9) 在等比数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若数列
,若数列![]() 也是等比数列,则
也是等比数列,则![]() 等于( ) (A)
等于( ) (A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
3.已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
(3)
记bn=![]() ,求{bn}数列的前项和Sn,并证明Sn+
,求{bn}数列的前项和Sn,并证明Sn+![]() =1.
=1.
一、选择题
1.在公比q![]() 1的等比数列{an}中,若am=p,则am+n的值为 ( )
1的等比数列{an}中,若am=p,则am+n的值为 ( )
(A)pqn+1 (B)pqn-1 (C)pqn (D)pqm+n-1
2.若数列{an}是等比数列,公比为q,则下列命题中是真命题的是 ( )
(A)若q>1,则an+1>an (B)若0<q<1,则an+1<an
(C)若q=1,则sn+1=Sn
(D)若-1<q<0,则![]()
3.在等比数列{an}中,a9+a10=a(a![]() ),a19+a20=b,则a99+a100的值为 ( )
),a19+a20=b,则a99+a100的值为 ( )
(A)![]() (B)(
(B)(![]() )9 (C)
)9 (C)![]() (D)(
(D)(![]() )10
)10
4.在2与6之间插入n个数,使它们组成等比数列,则这个数列的公比为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.若x,2x+2,3x+3是一个等比数列的连续三项,则x的值为 ( )
(A)-4 (B)-1 (C)1或4 (D)-1或-4
6.已知数列{an}是公比q![]() 的等比数列,给出下列六个数列:(1){kan}(k
的等比数列,给出下列六个数列:(1){kan}(k![]() ) (2){a2n-1} (3){an+1-an} (4){anan+1} (5){nan} (6){an3},其中仍能构成等比数列的个数为
) (2){a2n-1} (3){an+1-an} (4){anan+1} (5){nan} (6){an3},其中仍能构成等比数列的个数为
(A)4 (B)5 (C)6 (D)3 ( )
7.已知数列{an}的前n项和为Sn=b×2n+a(a![]() 0,b
0,b![]() 0),若数列{an}是等比数例,则a、b应满足的条件为 ( )
0),若数列{an}是等比数例,则a、b应满足的条件为 ( )
(A)a-b=0 (B)a-b![]() 0 (C)a+b=0 (D)a+b
0 (C)a+b=0 (D)a+b![]() 0
0
8.一个等比数列共有3n项,其前n项之积为A,次n项之积为B,末n项之积为C,则一定有(A)A+B=C (B)A+C=2B (C)AB=C (D)AC=B2 ( )
9.在等比数列{an}中,Sn=k-(![]() )n,则实数k的值为
(
)
)n,则实数k的值为
(
)
(A)1/2 (B)1 (C)3/4 (D)2
10.设{an}为等比数列,Sn=a1+…an,则在数列{Sn} 中 ( )
(A)任何一项均不为零 (B)必有一项为零
(C)至多有一项为零 (D)或有一项为零,或有无穷多项为零
11.在由正数组成的等比数列{![]() }中,若a4a5a6=3,log3a1+log3a2+log3a8+log3a9的值为
}中,若a4a5a6=3,log3a1+log3a2+log3a8+log3a9的值为
(A)![]() (B)
(B)![]() (C)2 (D)3
(C)2 (D)3![]() ( )
( )
12.在正项等比数列{an}中,a21+a22+……a2n=![]() ,则a1+a2+…an的值为 ( )
,则a1+a2+…an的值为 ( )
(A)2n (B)2n-1 (C)2n+1 (D)2n+1-2
13.数列{an}是正数组成的等比数列,公比q=2,a1a2a3……a20=a50,,则a2a4a6……a20的值为 (A)230 (B)283 (C)2170 (D)2102-2 ( )
14.在数列{an}中,a1=2,an+1=2an+2,则a100的值为 ( )
(A)2100-2 (B)2101-2 (C)2101 (D)215
15.某商品的价格前两年每年递增20%,后两年每年递减20%,最后一年的价格与原来的价格比较,变化情况是 ( )
(A)不增不减 (B)约增1.4% (C)约减9.2% (D)约减7.8%
二、填空题
1.在等比数列{an}中,a1-a5=-![]() ,S4=-5,则a4= 。
,S4=-5,则a4= 。
2.三个正数a,b,c成等比数列,且a+b+c=62,,lga+lgb+lgc=3,则这三个正数为
3.已知a>0,b>0,a![]() 在a与b之间插入n个正数x1,x2,…,xn,使a,x1,x2…,xn,b成等比数列,则
在a与b之间插入n个正数x1,x2,…,xn,使a,x1,x2…,xn,b成等比数列,则![]() =
=
4.已知首项为![]() ,公比为q(q>0)的等比数列的第m,n,k项顺次为M,N,K,则(n-k)log
,公比为q(q>0)的等比数列的第m,n,k项顺次为M,N,K,则(n-k)log![]() M+(k-m)log
M+(k-m)log![]() N+(m-n)log
N+(m-n)log![]() K=
K=
5.若数列{an}为等比数列,其中a3,a9是方程3x2+kx+7=0的两根,且(a3+a9)2=3a5a7+2,则实数k=
6.若2,a,b,c,d,18![]() 六个数成等比数列,则log9
六个数成等比数列,则log9![]() =
=
7.2+(2+22)+(2+22+23)+…+(2+22+23+…+210)=
8.某工厂在某年度之初借款A元,从该年度末开始,每年度偿还一定的金额,恰在n年内还清,年利率为r,则每次偿还的金额为 元。
三、解答题
1.已知等比数列{an},公比为-2,它的第n项为48,第2n-3项为192,求此数列的通项公式。
2.数列{an}是正项等比数列,它的前n项和为80,其中数值最大的项为54,前2n项的和为6560,求它的前100项的和。
3.已知a+b+c,b+c-a,c+a-b,a+b-c成等比数列,且公比为q,求证:(1)q3+
q 2+q=1,(2)q=![]()
4.已知数列{an}满足a1=1,a2=-![]() ,从第二项起,{an}是以
,从第二项起,{an}是以![]() 为公比的等比数列,{an}的前n项和为Sn,试问:S1,S2,S3…,Sn,…能否构成等比数列?为什么?
为公比的等比数列,{an}的前n项和为Sn,试问:S1,S2,S3…,Sn,…能否构成等比数列?为什么?
5.求Sn=(x+![]() )+(x2+
)+(x2+![]() )+…+(xn+
)+…+(xn+![]() )(y
)(y![]() )。
)。
6.某企业年初有资金1000万元,如果该企业经过生产经营,每年资金增长率为50%,但每年年底都要扣除消费基金x万元,余下资金投入再生产,为实现经过五年,资金达到2000万元(扣除消费基金后),那么每年扣除的消费资金应是多少万元(精确到万元)。
7.已知数列{an}满足a1=1,a2=r(r>0),数列{bn}是公比为q的等比数列(q>0),bn=anan+1,cn=a2n-1+a2n,求cn。
8.陈老师购买安居工程集资房7m2,单价为1000/ m2,一次性国家财政补贴28800元,学校补贴14400元,余款由个人负担,房地产开发公司对教师实行分期付款,即各期所付的款以及各期所付的款到最后一次付款时所生的利息合计,应等于个人负担的购房余款的现价以及这个余款现价到最后一次付款时所生利息之和,每期为一年,等额付款,签订购房合同后一年付款一次,再过一年又付款一次等等,若付10次,10年后付清。如果按年利率的7.5%每年复利一次计算(即本年利息计入次年的本金生息),那么每年应付款多少元?(参考数据:1.0759 ![]() 1.921,1.07510
1.921,1.07510![]() 2.065,1.07511
2.065,1.07511![]() 2.221)
2.221)
第八单元 等比数列
一、选择题CDACA BCDBD ABABD
二、填空题
1.1
2.50,10,2或2,10,50
3.![]()
4.0 5. ![]() 9 简解:a3+a9=-
9 简解:a3+a9=-![]() a3a9=a5a7=-
a3a9=a5a7=-![]() ∴ (-
∴ (-![]() )2=3×
)2=3×![]() +2
+2 ![]() k=
k=![]() 9
9
6、1
7.![]() 8、
8、![]()
二、 解答题
1.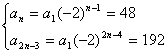
![]() 解得a1=3 ∴an=a1qn-1=3(-2)n-1 。
解得a1=3 ∴an=a1qn-1=3(-2)n-1 。
2.∵ S2n>Sn,
∴q![]() 1
1 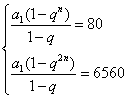
![]() ②/①,得qn=81 ③∴q>1,故前n项中an最大。③代入①,得a1=q-1
②/①,得qn=81 ③∴q>1,故前n项中an最大。③代入①,得a1=q-1
又由an=a1qn-1=54,得81a1=54q
∴a1=2,q=3 ∴S100=![]() 。
。
3.(1)q3+q2+q=![]()
(2)q=![]() 由合分比定理,可得q=
由合分比定理,可得q=![]()
4.当n![]() 2时,an=a2qn-2=-
2时,an=a2qn-2=-![]() (
(![]() )n-2=-(
)n-2=-(![]() )n-1 ∴an=
)n-1 ∴an=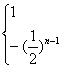
![]()
当n=1时,S1=a1=1
当n![]() 2时,Sn=a1+a2+…+an=1-
2时,Sn=a1+a2+…+an=1-![]() -(
-(![]() )2-…-(
)2-…-(![]() )n-1=1-[
)n-1=1-[![]() +(
+(![]() )2+…+(
)2+…+(![]() )n-1]=1-
)n-1]=1-
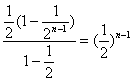
∴Sn=(![]() )n-1
)n-1 ![]()
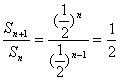
![]() {Sn}可以构成等比数列。
{Sn}可以构成等比数列。
5、当x![]() 1,y
1,y![]() 1时,
1时,
∴Sn=(x+x2+…+xn)+(![]() +
+![]() )=
)=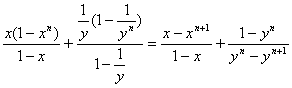
当x=1,y![]() 1时 Sn=n+
1时 Sn=n+![]()
当x![]() 1,y=1时 Sn=
1,y=1时 Sn=![]()
当x=y=1时 Sn=2n
6.设an表示第n年年底扣除消费基金后的资金。
a1=1000(1+![]() )-x
)-x
a2=[1000(1+![]() )-x](1+
)-x](1+![]() )-x=1000(1+
)-x=1000(1+![]() )2-x(1+
)2-x(1+![]() )-x
)-x
a3=[1000(1+![]() )2-x(1+
)2-x(1+![]() )-x](1+
)-x](1+![]() )-x=1000(1+
)-x=1000(1+![]() )3-x(1+
)3-x(1+![]() )2-x(1+
)2-x(1+![]() )-x
)-x
类推所得
a5=1000(1+![]() )5-x(1+
)5-x(1+![]() )4-x(1+
)4-x(1+![]() )3-x(1+
)3-x(1+![]() )2-x(1+
)2-x(1+![]() )-x
)-x
则1000(![]() )5-x[(
)5-x[(![]() )4+(
)4+(![]() )3+…+1]=2000即1000(
)3+…+1]=2000即1000(![]() )5-x·
)5-x·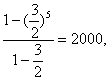
解得x![]() 424万元
424万元
7、∵bn+1=bnq,
∴an+1an+2=anan+1q ∴an+2=anq,即![]()
由a1=1,a3=q,a5=q2,……,知奇数项构成一个等比数列,故a2n-1=qn-1
由a2=r,a4=rq,a6=rq2,……,知偶数项也构成一个等比数列,故a2n=rqn-1
∴Cn=(1+r)qn-1
8、设每年付款x元,那么10年后
第一年付款的本利和为a1=1.0759x元。
第二年付款的本利和为a2=1.0758x元。
依次类推
第n年付款的本利和为an=1.07510-nx元。
则各年付款的本利和{an}为等比数列。
∴10年付款的本利和为S10=![]() 。
。
个人负担的余额总数为72×1000-28800-14400=28800元。
10年后余款的本利和为18800×1.07510
∴![]() 解得x=
解得x=![]()