高一数学同步测试（12）—等比数列
一、选择题：
1．{an}是等比数列，下面四个命题中真命题的个数为 （ ）
①{an2}也是等比数列 ②{can}(c≠0)也是等比数列
③{
}也是等比数列 ④{lnan}也是等比数列
A．4 B．3 C．2 D．1
2．等比数列{a n }中，已知a9 =－2，则此数列前17项之积为 （ ）
A．216 B．－216 C．217 D．－217
3．等比数列｛an｝中，a3=7，前3项之和S3=21， 则公比q的值为 （ ）
A．1 B．－
C．1或－1 D．－1或
4．在等比数列{an}中，如果a6=6，a9=9，那么a3等于 （ ）
A．4 B．
C．
D．2
5．若两数的等差中项为6，等比中项为5，则以这两数为两根的一元二次方程为 （ ）
A．x2－6x＋25=0 B．x2＋12x＋25=0
C．x2＋6x－25=0 D．x2－12x＋25=0
6．某工厂去年总产a，计划今后5年内每一年比上一年增长10%，这5年的最后一年该厂的总产值是 （ ）
A．1.1 4 a B．1.1 5 a C．1.1 6 a D． (1＋1.1 5)a
7．等比数列{an}中，a9＋a10=a(a≠0)，a19＋a20=b，则a99＋a100等于 （ ）
A．
B．(
)9 C．
D．()10
8．已知各项为正的等比数列的前5项之和为3，前15项之和为39，则该数列的前10项之和为 （ ）
A．3
B．3
C．12 D．15
9．某厂2001年12月份产值计划为当年1月份产值的n倍，则该厂2001年度产值的月平均增长率为 （ ）
A．
B．
C．
D．
10．已知等比数列
中，公比
，且
，那么
等于
（ ）
A．
B．
C．
D．
11．等比数列的前n项和Sn=k·3n＋1，则k的值为 （ ）
A．全体实数 B．－1 C．1 D．3
12．某地每年消耗木材约20万
，每价240元，为了减少木材消耗，决定按
征收木材税，这样每年的木材消耗量减少
万，为了既减少木材消耗又保证税金收入每年不少于90万元，则
的范围是 （ ）
A．[1，3] B．[2，4] C．[3，5] D．[4，6]
二、填空题：
13．在等比数列{an}中，已知a1=，a4=12，则q=_____ ____，an=____ ____．
14．在等比数列{an}中，an＞0，且an＋2=an＋an＋1，则该数列的公比q=___ ___．
15．在等比数列｛an｝中，已知a4a7＝－512，a3＋a8＝124，且公比为整数，求a10＝ ．
16．数列｛
｝中，
且
是正整数)，则数列的通项公式
．
三、解答题：
17．已知数列满足a1=1，an＋1=2an＋1(n∈N*)
(1) 求证数列{an＋1}是等比数列；
(2) 求{an}的通项公式．
18．在等比数列｛an｝中，已知对n∈N*，a1＋a2＋…＋an＝2n－1，求a12＋a22＋…＋an2．
19．在等比数列｛an｝中，已知Sn＝48，S2n＝60，求S3n．
20．求和：Sn＝1＋3x＋5x2＋7x3＋…＋(2n－1)xn－1(x≠0)．
21．在等比数列｛an｝中，a1＋an=66，a2·an－1=128，且前n项和Sn=126，求n及公比q．
22．某城市1990年底人口为50万，人均住房面积为16 m2，如果该市每年人口平均增长率为1%，每年平均新增住房面积为30万 m2，求2000年底该市人均住房的面积数．(已知1.015≈1.05，精确到0.01 m2)
参考答案
一、选择题： BDCAD BACDB BC
二、填空题：13.2， 3·2n－2． 14.
．15.512 ．16.
．
三、解答题：
17.(1)证明： 由an＋1=2an＋1得an＋1＋1=2(an＋1)
又an＋1≠0 ∴
=2
即{an＋1}为等比数列．
(2)解析： 由(1)知an＋1=(a1＋1)qn－1
即an=(a1＋1)qn－1－1=2·2n－1－1=2n－1
18.解析： 由a1＋a2＋…＋an＝2n－1 ①
n∈N*知a1＝1
且a1＋a2＋…＋an－1＝2n－1－1 ②
由①－②得an＝2n－1，n≥2
又a1＝1，∴an＝2n－1，n∈N*
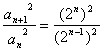＝4
即｛an2｝为公比为4的等比数列
∴a12＋a22＋…＋an2＝
19.解析一： ∵S2n≠2Sn，∴q≠1
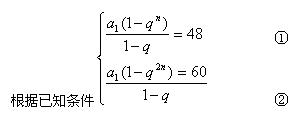
②÷①得：1＋qn＝
即qn＝
③
③代入①得
＝64 ④
∴S3n＝
(1－q3n)＝64(1－
)＝63
解析二： ∵｛an｝为等比数列
∴(S2n－Sn)2＝Sn(S3n－S2n)
∴S3n＝
＋60＝63
20.解析：当x=1时，Sn=1＋3＋5＋…＋(2n－1)=n2
当x≠1时，∵Sn=1＋3x＋5x2＋7x3＋…＋(2n－1)xn－1， ①
等式两边同乘以x得：
xSn=x＋3x2＋5x3＋7x4＋…＋(2n－1)xn． ②
①－②得：
(1－x)Sn=1＋2x(1＋x＋x2＋…＋xn－2)－(2n－1)xn=1－(2n－1)xn＋
，
∴Sn=
．
21.解析：∵a1an=a2an－1=128，又a1＋an=66，
∴a1、an是方程x2－66x＋128=0的两根，解方程得x1=2，x2=64，
∴a1=2，an=64或a1=64，an=2，显然q≠1．
若a1=2，an=64，由
=126得2－64q=126－126q，
∴q=2，由an=a1qn－1得2n－1=32， ∴n=6．
若a1=64，an=2，同理可求得q=，n=6．
综上所述，n的值为6，公比q=2或．
22.解析：依题意，每年年底的人口数组成一个等比数列{an}：a1=50，q=1＋1%=1．01，n=11
则a11=50×1．0110=50×(1．015)2≈55.125(万)，
又每年年底的住房面积数组成一个等差数列{bn}：b1=16×50=800，d=30，n=11
∴b11=800＋10×30=1100(万米2)
因此2000年底人均住房面积为：1100÷55.125≈19．95(m2)