高一数学秋季学期期末考试
高一数学（示范高中卷）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分．考试时间120分钟．
说明：可以使用计算器，但未注明精确度的计算问题不得采取近似计算，建议根据题型特点把握好使用计算器的时机．相信你一定会有出色的表现！
第Ⅰ卷
本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．请把符合题目要求的选项的字母填入答题卷的答题卡中．
一、选择题：
1．不等式｜2－x｜≥1的解集是
（A）｛x｜1≤x≤3｝ （B）｛x｜x≤1或x≥3｝
（C）｛x｜x≤1｝ （D）｛x｜x≥3｝
2．设A＝｛x｜x2－5x＋4≤0｝，B＝｛x｜x2－5x＋6≥0｝，则A∩B
（A）［1，2］
［3，4］ （B）［1，2］
［3，4］
（C）｛1，2，3，4｝ （D）［－4，－1］［2，3］
3．命题“若x2＋y2＝0，则x、y全为0”的逆否命题是
（A）若x、y全为0，则x2＋y2≠0 （B）若x、y不全为0，则x2＋y2＝0
（C）若x、y全不为0，则x2＋y2≠0 （D）若x、y不全为0，则x2＋y2≠0
4．如果a，b，c都是实数，那么P：ac＜0，是q：关于x的方程ax2＋bx＋c＝0有一个正根和一个负根的
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
5．f（x）是一次函数且2f（1）＋3f（2）＝3，2f（－1）－f（0）＝－1，则f（x）等于
（A）
（B）36x－9 （C）
（D）9－36x
6．已知三个命题：①方程x2－x＋2＝0的判别式小于或等于零；②若｜x｜≥0，则x≥0；
③5＞2且3＜7．其中真命题是
（A）①和② （B）①和③ （C）②和③ （D）只有①
7．已知函数f（x）＝
那么
的值为
（A）9 （B）
（C）－9 （D）－
8．若定义在（－1，0）内的函数f（x）＝log2a（x＋1）＞0，则a的取值范围是
（A）
（B）
（C）
（D）
9．设｛an｝为递增等差数列，前三项的和为12，前三项的积为48，则它的首项为
（A）1 （B）2 （C）4 （D）6
10．若｛an｝是等比数列，且an＞0，a2a4＋2a3a5＋a4a6＝25，则a3＋a5的值为
（A）5 （B）10 （C）15 （D）20
11．若数列｛an｝是公差为
的等差数列，它的前100项和为145，则a1＋a3＋a5＋…＋a99的值是
（A）60 （B）72.5 （C）85 （D）120
12．若2x－3－x≥2－y－3y，则
（A）x－y≥0 （B）x－y≤0 （C）x＋y≥0 （D）x＋y≤0
第Ⅱ卷（本卷共10小题，共90分）
二、填空题：本大题共4小题；每小题4分，共16分．请将答案填写在答题卷中的横线上．
13．（x，y）在映射f下的象是（xy，x＋y），则点（2，3）在f下的象是▲．
14．若f（10x）＝x，则f（5）＝▲．
15．若数列｛an｝满足an＋1＝
且a1＝0，则a7＝▲．
16．若函数y＝
（x≤－1），则f－1（2）＝▲．
高一数学（示范高中卷）
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 1～12 | 13～16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 得分 |
|
|
|
|
|
|
|
|
|
一、选择题答题卡：（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
| 得分 | 评卷人 |
|
|
|
二、填空题：（每小题4分，共16分）
13． ； 14． ； 15． ； 16． ．
三、解答题：本大题共6小题；共74分．解答应写出文字说明、证明过程或演算步骤．
| 得分 | 评卷人 |
|
|
|
17．（本小题满分12分）
求（lg2）2＋lg2·lg50＋lg25的值．
18．（本小题满分12分）
得分 | 评卷人 |
|
|
|
已知集合A＝｛2，－1，x2－x＋1｝，B＝｛2y，－4，x＋4｝，C＝｛－1，7｝，且A∩B＝C，求实数x，y的值．
| 得分 | 评卷人 |
|
|
|
19．（本小题满分12分）
判断函数f（x）＝
在区间（1，＋∞）上的单调性，并用单调性定义证明．
20．（本小题满分12分）
| 得分 | 评卷人 |
|
|
|
数列｛an｝，Sn为它的前n项的和，已知a1＝－2，an＋1＝Sn，当n≥2时，求：an和Sn．
| 得分 | 评卷人 |
|
|
|
21．（本小题满分12分）
已知一扇形的周长为c（c＞0），当扇形的弧长为何值时，它有最大面积？并求出面积的最大值．
22．（本小题满分14分）
| 得分 | 评卷人 |
|
|
|
已知函数f（x）＝log2（x＋m），且f（0）、f（2）、f（6）成等差数列．
（1）求实数m的值；
（2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f（a）＋f（c）与2f（b）的大小关系，并证明你的结论．
高一数学（示范高中卷）参考答案及评分标准
一、选择题：（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | D | C | C | B | B | A | B | A | A | C |
二、填空题：（每小题4分，共16分）
13．（6，5） 14．lg5 15．4 16．－
三、解答题：
17．解：原式＝（lg2）2＋lg2·（lg2＋2lg5）＋2lg5···································································· 2分
＝2（lg2）2＋2lg2·lg5＋2lg5······················································································ 4分
＝2lg2（lg2＋lg5）＋2lg5······························································································· 6分
＝2lg2＋2lg5·························································································································· 8分
＝2（lg2＋lg5）················································································································ 10分
＝2．······································································································································ 12分
18．解：∵A∩B＝C，且C＝｛－1，7｝，∴7∈A，－1∈B，7∈B．······························· 2分
∵A＝｛2，－1，x2－x＋1｝，∴x2－x＋1＝7，··························································· 4分
∴x＝3或x＝－2．····················································································································· 6分
当x＝－2时，B＝｛2y，－4，2｝，
与－1∈B，7∈B矛盾．··········································································································· 8分
当x＝3时，B＝｛2y，－4，7｝，
∴2y＝－1．∴y＝－．······································································································· 10分
∴
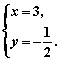··································································································································· 12分
19．解：f（x）在区间（1，＋∞）上是减函数．证明如下：··············································· 2分
取任意的x1，x2∈（1，＋∞），且x1＜x2，则································································· 3分
f（x1）－f（x2）＝
－
＝
＝
． 5分
∵x1＜x2，∴x2－x1＞0．··········································································································· 6分
又∵x1，x2∈（1，＋∞），∴x2＋x1＞0，
－1＞0，
－1＞0，·················· 8分
∴（－1）（－1）＞0．（x2＋x1）（x2－x1）＞0············································· 10分
∴f（x1）－f（x2）＞0．········································································································· 11分
根据定义知：f（x）在区间（1，＋∞）上是减函数．·········································· 12分
20．解：∵an＋1＝Sn，又∵an＋1＝Sn＋1-Sn，∴Sn＋1＝2Sn．······················································· 2分
∴｛Sn｝是以2为公比，首项为S1＝a1＝－2的等比数列．································· 6分
∴Sn＝a1×2n-1＝－2n．··········································································································· 10分
∵当n≥2时，an＝Sn－Sn-1＝－2n-1．············································································ 12分
21．解：设扇形的半径为R，弧长为l，面积为S
∵c＝2R＋l，∴R＝
（l＜c）．······················································································ 3分
则S＝Rl＝×·l＝
（cl－l2）········································································· 5分
＝－（l2－cl）＝－（l－
）2＋
．···································································· 7分
∴当l＝时，Smax＝．···································································································· 10分
答：当扇形的弧长为时，扇形有最大面积，扇形面积的最大值是． 12分
22．解：（1）由f（0）、f（2）、f（6）成等差数列，
可得2log2（2＋m）＝log2m＋log2（6＋m），····················································· 3分
即（m＋2）2＝m（m＋6），且m＞0，解得m＝2．······································ 5分
（2）由f（x）＝log2（x＋2），
可得2f（b）＝2log2（b＋2）＝log2（b＋2）2，················································ 6分
f（a）＋f（c）＝log2（a＋2）＋log2（c＋2）
＝log2［（a＋2）（c＋2）］，····························································· 7分
∵a、b、c成等比数列，∴b2＝ac．········································································· 8分
又a、b、c是两两不相等的正数，
故（a＋2）（c＋2）－（b＋2）2
＝ac＋2（a＋c）＋4－（b2＋4b＋4）···························································· 10分
＝2（a＋c－2
）＝2
＞0，···················································· 12分
∴log2［（a＋2）（c＋2）］＞log2（b＋2）2．····················································· 13分
即f（a）＋f（c）＞2f（b）．···················································································· 14分