高一级数学上期考试试卷
一、选择题（单项选择，每小题5分，共60分）
1．sin(-11400)的值是（ ）
A 
B 
C 
D 
2．已知
为单位向量，则下列正确的是（ ）
A 
B 
C 
D 
3．设
，若
共线，则k等于( )
A 3 B 0 C -5 D 3或-5
4．
（ ）
A 0
B -1
C 
D 1
5．函数
的最小正周期是（ ）
A 
B 
C 
D 
6．有以下结论：
（1）若
,且
，则
（2）
（3）
（4）函数
的图象可由函数
的图象按向量
平移而得到。
其中错误的结论是（ ）
A （1）（2） B （3）（4） C （1）（3） D （2）（4）
7．三角形ABC中，
则
的值是（ ）
A 1
B -1
C 0
D 
8．已知
=（-2，-3）、
＝（1，1），点
在线段MN的中垂线上，
则x等于（ ）．
A．
B．
C．
D．
9．在三角形ABC中，
是B-A<0的（ ）
A 充分不必要条件 B 必要不充分条件
C 充要条件 D 既不充分也不必要的条件
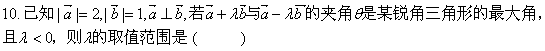A 
B 
C 
D 
11．在三角形ABC中，已知
则向量
在向量
的投影是（ ）
A 7 B 6 C 5 D 4
12．把函数
的图象向右平移a个单位，所得图象关于y轴对称，则a的最大负值是( )
A 
B 
C 
D 
二、填空题（每小题6分，共24分）
13．
_____________________ .
15．已知三角形ABC中，
则
与
的夹角是_________________________ .
16．给出下列8种图象的变换方法：
（1） 将图象上所有点的横坐标缩短到原来的倍（纵坐标不变）。
（2） 将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）；。
（3） 将图象上所有点的纵坐标伸长到原来的3倍（横坐标不变）；。
（4） 将图象上所有点的纵坐标缩短到原来的
倍（横坐标不变）；。
（5） 将图象向左平移
个单位。
（6）将图象向右平移个单位。
（7）将图象向左平移
个单位。
（8）将图象向右平移个单位。
需要且只要用上述3种变换可由函数
的图象得到
的图象，那么这3种变换正确的顺序是
___________________________（填上一组正确的序号即可）
高2008级上期数学试卷
班级_______________学号_______________姓名________________
一、选择题（单项选择，每小题5分，共60分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题（每小题6分，共24分）
13. ________________________________ .
14. _________________________ ；_________________________ .
15. ________________________________ .
16. _________________________________ .
三 解答题（共66分）
17．（13分）
18．（13分）已知
的值；
（2）求
的值。
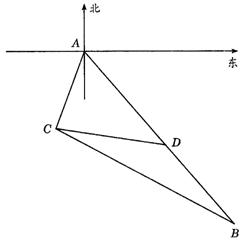
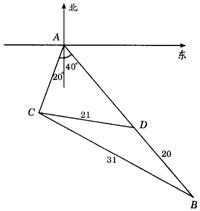
19．（13分）如图，某观测站C在城A的南偏西
方向上，从城A出发有一条公路，走向是南偏东
，在C处测得距离C处31千米的公路上的B处有一辆正沿着公路向城A驶去，行驶了20千米后到达D处，测得C、D二处间距离为21千米，这时此车距城A多少千米？
20. （13分）已知，
，
，
，且
，求证
．
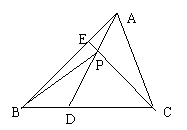
22．（14分）在三角形ABC中，点D分
之比为1：2，点E分
分之比为2：1，设
，
。
（1）
（2）试用表示
；
(3) 在边AC上有F点，使得
，求证：B,P,F三点共线。
 |
答 案
一．选择题
DCDAD CBACC AD
7.△ABC为等腰直角三角形，，且
，=
8．
，
，中点为
．
＝（1，1）-（-2，-3）＝（3，4），
．∵ 
，∴ 
，∴ 
．
9. 
10．
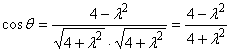
由
可解得。
11．
，由余弦定理得
12．=2
向右平移
个单位得
它关于y轴对称，
，当k=1时，
二、填空题
13．
14.
15.
16. 方案一：（5）（1）（3）或(3) (5) (1)或（5）（3）（1）
方案二：（1）（7）（3）或（3）（1）（7）或（1）（3）（7）
三、解答题
17．解：
……3分
又
…… 7分
=
…… 13分
18．解：
=
=
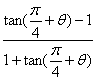…… 2分
又
……4分
|
……6分
（2）如图
…… 13分
19．解：在
中，
，
，
，
由余弦定理得:
所以
．……4分
在
中，CD＝21，
．……9分
由正弦定理得
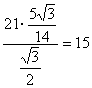（千米）．所以此车距城A有15千米． ……13分
20．证明：要证，
只需证
， ……3分
只需证
． ……5分
∵，，，
∴
，
，
，……9分
∴
，
∴
成立．
∴． ……13分
21.由题意
……2分
① ……4分
（2）设
② ……6分
由①、②得，
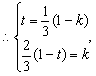解得
……9分
（3）由
，得
……11分
，即
与
共线 ……13分
又与有公共点B，
三点共线。……14分