高一(下)数学期末试卷
一、选择题:本大题共10小题,每小题5分,共50分.)
1.已知向量![]() 、
、![]() 满足:
满足:![]() +
+![]() =
=![]() ,
,![]() -
-![]() =
=![]() ,则
,则![]() 、
、![]() 的坐标分别为 ( C )
的坐标分别为 ( C )
A.![]()
![]() B.
B.![]()
![]()
C.![]()
![]() D.
D.![]()
![]()
2.已知扇形面积为![]() ,半径是1,则扇形的圆心角是 (C)
,半径是1,则扇形的圆心角是 (C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列向量中,能作为表示它们所在平面内的所有向量的基底的是 ( B )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
4.已知函数![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为
(C)
的值为
(C)
A.3 B.4 C.5 D.6
5. 已知向量![]() ,
,![]() ,则
,则![]() 的值是( D )
的值是( D )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
6.已知![]() ( D )
( D )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
7.![]() 是两个单位向量,且夹角为120°,则
是两个单位向量,且夹角为120°,则![]() ·
·![]() 的值为( A )
的值为( A )
A.-10 B.-5 C.5 D.10
8.函数![]() 的图象的一条对称轴的方程是( A).
的图象的一条对称轴的方程是( A).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知函数![]() 在同一周期内,当
在同一周期内,当![]() 时,取得最大值
时,取得最大值![]() ,当
,当![]() 时,取得最小值
时,取得最小值![]() ,则函数的解析式为
( D )
,则函数的解析式为
( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.如右图所示,两射线![]() 与
与![]() 交于
交于![]() ,则下列选项中哪些向量的终点落在阴暗区域内
,则下列选项中哪些向量的终点落在阴暗区域内
( A )
①![]() ②
②![]()
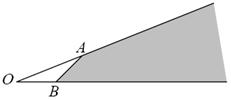 ③
③![]() ④
④![]()
⑤![]()
A.①② B.①②④ C.①②③④ D.③⑤
二.填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上
11.已知点P分有向线段![]() 的比为-3,那么点P1分
的比为-3,那么点P1分![]() 的比是 .
的比是 .![]()
12.把函数![]() 的图象按向量
的图象按向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 的坐标是 (
的坐标是 (![]() ,1)
,1)
13.若角![]() 终边在直线
终边在直线![]() 上,顶点为原点,且
上,顶点为原点,且![]() ,又知点
,又知点![]() 是角
是角![]() 终边上一点,且
终边上一点,且![]() ,则
,则![]() 的值为
.2
的值为
.2
14.已知![]() 是第二象限角,且
是第二象限角,且![]() ,则
,则![]() 的值是
的值是
![]()
15.关于![]() 的方程
的方程![]() 内有相异两实根,则
内有相异两实根,则![]() 的取值范围为 [0,1)
的取值范围为 [0,1)
16、给出下列命题:
(1)![]() ∥
∥![]() 的充要条件是存在唯一的实数
的充要条件是存在唯一的实数![]() 使
使![]() =
=![]()
![]() ;
;
(2)若α、β是第一象限角,且α>β,则cosα<cosβ;
(3)函数y=sin(![]() x-
x-![]() )是偶函数;
)是偶函数;
(4) 向量![]() 与向量
与向量![]() 的方向相反,是
的方向相反,是![]() 与
与![]() 是共线向量的充分不必要条件;
是共线向量的充分不必要条件;
(5)函数y=sin2x的图象向右平移![]() 个单位,得到y=sin(2x-
个单位,得到y=sin(2x-![]() ))的图象.
))的图象.
其中正确的命题的序号是 . 34
三、解答题(本大题共6个小题,共70分)
17.(本小题满分12分) 已知![]() .
.
(1)求![]() 的值;
(2)求
的值;
(2)求![]() 的值.
的值.
解:![]() (2分)
(2分)
(1)![]() (5分)由已知
(5分)由已知![]() 有
有![]() ,
,![]() . (6分)
. (6分)
(2)由(1)可求得:![]() (9分)
(9分)
![]() (12分)
(12分)
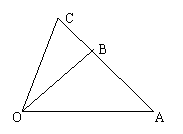 18.(本题满分12分)如图,已知向量
18.(本题满分12分)如图,已知向量![]() ,
,![]() ,
,
![]() ,且
,且![]() .(Ⅰ)试用
.(Ⅰ)试用![]() 表示
表示![]() ;
;
(Ⅱ)若点![]()
![]() 、
、![]()
![]() ,O(0,0)求点
,O(0,0)求点![]() 坐标.
坐标.
解:(Ⅰ)由题意得: ![]() ,
,![]() ,———————2分
,———————2分
又
![]()
∴
![]() ———————————4分
———————————4分
解得:
![]() ———————————6分
———————————6分
(Ⅱ) 由![]() 可知:点
可知:点![]() 分有向线段
分有向线段![]() 所成的比为2,———8分
所成的比为2,———8分
设点![]()
![]() ,则得:
,则得:
![]() ,
,![]() —————————10分
—————————10分
解得:
![]() ,
,![]() ,
,
∴
点![]() 坐标为
坐标为![]() .———————————12分
.———————————12分
19.(本大题满分12分) 已知函数![]()
(1)写出函数的单调递减区间;
(2)设![]() ,f (x)的最小值是-2,最大值是
,f (x)的最小值是-2,最大值是![]() ,求实数a、b的
,求实数a、b的
(1)解:![]()
![]() 4分
4分
∵a>0,x∈R,∴f (x)的递减区间是![]() (k∈Z) 6分
(k∈Z) 6分
(2)解:∵x∈[0,![]() ],∴2x∈[0,
],∴2x∈[0,![]() ],2x-
],2x-![]() ∈[
∈[![]() ] 7分
] 7分
∴![]() 9分
9分
∴函数f (x)的最小值是![]() ,最大值是
,最大值是![]() 10分
10分
由已知得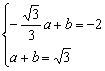 , 解得a=2,b=
, 解得a=2,b=![]() 12分
12分
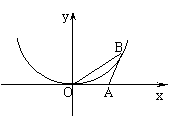 20.(本题满分14分)如图,△
20.(本题满分14分)如图,△![]() 的顶点
的顶点![]() 在
在![]() 正半轴上,顶点
正半轴上,顶点![]() 在第一象限内,又知△
在第一象限内,又知△![]() 的面积为
的面积为![]() ,
,![]() .
.
(Ⅰ)若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,求
,求
实数![]() 的取值范围;
的取值范围;
|
解:(Ⅰ)根据题意:![]()
即 ![]() ,—————————2分
,—————————2分
又 ![]()
以上两式相除,并整理得:
![]() ———————————4分
———————————4分
∵![]() ,∴
,∴![]()
∴实数![]() 的取值范围是
的取值范围是![]() . ———————————6分
. ———————————6分
|
![]() ,
,
于是
![]() ,
,![]() ,——————8分
,——————8分
又 ![]()
![]()
∴
![]() ,
———————————10分
,
———————————10分
从而 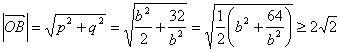 ,当且仅当
,当且仅当![]() 即
即![]() 时,取等号, ———————————12分
时,取等号, ———————————12分
此时,点![]() ,代入
,代入![]() 解得
解得![]() ,
,
∴ ![]() 取得最小值
取得最小值![]() 时,
时,![]() . ——————14分
. ——————14分
(Ⅱ)解二:∵ ![]() ,
,
|
∴ 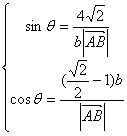 ,
,
∴ 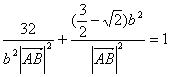 ,
,
即 ![]() ,———————10分
,———————10分
∴ ![]() ,
,
当且仅当![]() 即
即![]() 时,取等号,—————————12分
时,取等号,—————————12分
此时,点![]() ,
,
由![]() 求得点
求得点![]() 纵坐标
纵坐标![]() ,
,
代入 ![]() 求得点
求得点![]() ,
,
代入 ![]() 解得
解得![]() ,
,
∴ ![]() 取得最小值
取得最小值![]() 时,
时,![]() .———————14分
.———————14分
21.(本题满分10分)
已知![]() ,
,![]() ,
,![]() ,
,![]() ,试比较
,试比较![]() 、
、![]() 、
、![]() 的大小.
的大小.
【解答】不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() 由此猜想
由此猜想![]()
由![]() 得
得![]() ,
,![]() 得
得![]() ,……5分
,……5分
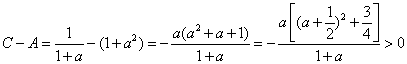 得
得![]() ,…..9分
,…..9分
即得![]() .………………………………………………………………………..10分
.………………………………………………………………………..10分
22. (本小题10分)解关于x的不等式![]() >x,(a∈R).
>x,(a∈R).
解:由![]() >x得
>x得![]() -x>0即
-x>0即![]() >0(2分)
>0(2分)
此不等式与x(ax-1)>0同解.(3分)
![]()
![]() x>0 x<0
x>0 x<0
①若a<0,则 或
ax-1>0 ax-1<0
得: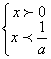 或
或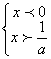
即 无解 或![]() <x<0. ∴解集为(
<x<0. ∴解集为(![]() ,0).(4分)
,0).(4分)
②若a=0,则-x>0![]() x<0,∴解集为(-∞,0).(6分)
x<0,∴解集为(-∞,0).(6分)
![]()
![]() x>0 x<0
x>0 x<0
③若a>0,则 或
ax-1>0 ax-1<0
得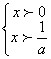 或
或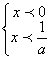
即:x>![]() 或x<0,∴解集为(-∞,0)∪(
或x<0,∴解集为(-∞,0)∪(![]() ,+∞)(9分)
,+∞)(9分)
综上所述:①当a<0时,不等式的解集是(![]() ,0)
,0)
②当a=0时,不等式的解集是(-∞,0)
③当a>0时,不等式的解集是(-∞,0)∪(![]() ,+∞)(10分)
,+∞)(10分)