第五十课时 三角函数单元测试题(二)
姓名 班级 学号 成绩
一、选择题:(50分)
1、函数![]() 的值域为
( )
的值域为
( )
A、![]() B、
B、![]() C、
C、![]() D、
都不对
D、
都不对
2、 已知函数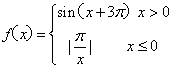 ,则
,则![]()
A、![]() B、-
B、-![]() C、
C、![]() D、
D、![]()
3、若![]() ,则
,则![]() ( )
( )
A、 ![]() B、-
B、-![]() C、
C、![]() D、-
D、-![]()
4、函数![]() 在定义域内是
( )
在定义域内是
( )
A、增函数 B、减函数 C、有增有减 D、无单调性
5、函数![]() ( )
( )
A、[-1,1] B、![]() C、
C、![]() D、
D、![]()
6、若![]() ,则
,则![]() =
( )
=
( )
A、2
B、-2
C、![]() D、
D、![]()
7、要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象( )
的图象( )
A、左移![]() B、右移
B、右移![]() C、左移
C、左移![]() D、右移
D、右移![]()
8、同时具有以下性质:(1)最小正周期是![]() ;(2)图象关于直线
;(2)图象关于直线![]() 对称;(3)在
对称;(3)在![]() 上是增函数,这样的一个函数是
( )
上是增函数,这样的一个函数是
( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
 9、函数
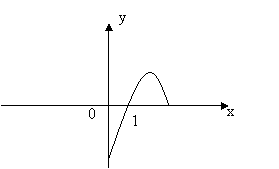
9、函数![]() 的定义域在(-3,3)上的奇函数,当
的定义域在(-3,3)上的奇函数,当![]() 时,
时,![]() 的图象如右图,则不等式
的图象如右图,则不等式![]() 的解集是
( )
的解集是
( )
A、![]()
B、![]()
C、![]()
D、![]()
10、若函数![]() 满足
满足![]() ,且
,且![]() ,则函数
,则函数 ![]() 的图象与函数
的图象与函数![]() 的图象的交点个数为
(
)
的图象的交点个数为
(
)
A、2 B、3 C、4 D、无数个
二、填空题(30分)
11、 若![]() ,且
,且![]() ,则
,则![]() 。
。
12、式子![]() 的值 0。(
的值 0。(![]() )
)
13、函数![]() ,且对于任意的
,且对于任意的![]() 都有
都有![]() ,
,
则![]()
14、函数![]() 的最小值为
的最小值为
15、函数![]() ,比较
,比较![]()
![]() 大小。
大小。
16、函数![]() 为奇函数,则
为奇函数,则![]() 。
。
三角函数单元测试题
姓名 班级 学号 成绩
一、选择题:(50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(30分)
11、 。12 。13 。
14、 。15 。16 。
三、解答题
17(本题满分14分)、已知![]()
(1)求![]() 值;
值;
(2)求![]() 值;
值;
18(本题满分14分)、已知函数![]() )的图象在`Y轴上的交点(0,1),在相邻两最值点
)的图象在`Y轴上的交点(0,1),在相邻两最值点![]() 上取最值。
上取最值。
(1)
求![]() 的解析式
的解析式
(2)
若![]() 的最大值和最小值分别为6和2,求
的最大值和最小值分别为6和2,求![]() 的值?
的值?
19(本题满分14分)已知函数![]() 的一条对称轴是直线
的一条对称轴是直线![]()
(1)求![]()
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)画出函数![]() 在区间
在区间![]() 上的图象
上的图象
20(本题满分14分)、若![]()
(1)求![]() 的对称轴方程、对称点坐标
的对称轴方程、对称点坐标
(2)求![]() 的单调增区间
的单调增区间
(3)若![]() =
=![]() ,求
,求![]() 的值
的值
21(本题满分14分)、在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋。下面给出某港口在某季节每天几个时刻的水深
| 时间 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 水深 | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
(1) 选用一个三角形来近似描述这个港口的水深与时间的函数关系
(2) 求水深能达到6.25m的时刻
(3) 一条货船的吃水深度为5m,安全条例规定至少要有1.25m的安全间隙,该怎样设计进、出港口的时间表,以确保卸货的同时船舶也安全。