高一数学上学期质量检测卷（附答案）
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的.
1．已知全集U={0，2，4，6，8，10}，集合A={2，4，6}，B＝{1}，则
UA∪B等于A
A．{0，1，8，10} B． {1，2，4，6}
C. {0，8，10} D. Φ
2.下列幂函数中过点(0,0),(1,1)的偶函数是 B
A.
B. 
C.
D.
3．映射f:A→B，在f作用下A中元素
与B中元素
对应，则与B中元素
对应的A中元素是 C
A．
B. 
C.
D.
4．若
，则函数y =ax－1的图象一定过点 B
A． (0,1) B. (1,1) C. (1,0) D. (0,-1)
5．某学生从家里去学校上学，骑自行车一段时间，因自行车爆胎，后来推车步行，下图中横轴表示出发后的时间，纵轴表示该生离学校的距离，则较符合该学生走法的图是 D
 |
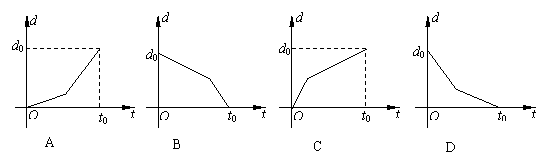6．函数y=
的单调递减区间是 A
A．（-∞，-3） B．(-1，+∞) C．（-∞，-1 ） D．[-1，+∞)
7.已知集合
，
，若
，则a的取值范围是 C
A. 
B.
(-1, +∞) C. [-1, +∞)
D. [-1,1]
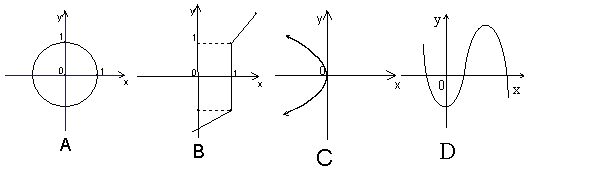8.如下图，可表示函数
的图象的只能是 D
9．若函数f(x)是定义在[-6，6]上的偶函数，且在[-6，0]上单调递减，则 D
A．f(3)+f(4)>0 B． f(-3)-f(-2)<0
C．f(-2)+f(-5)<0 D． f(4)-f(-1)>0
10．已知函数f（x）是R上的增函数，A（0，-2），B（3，2）是其图象上的两点，那么
f（x+1）＜2的解集是 B
A．（1，4） B．（-1，2）
C．（-∞，1）∪［4，+∞) D．（-∞，-1）∪［2，+∞)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | C | B | D | A | C | D | D | B |
二、 填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）
11、三个数60．7，0．76，log0．76的大小关系是60．7＞0．76＞log0．76
12．设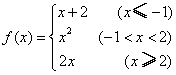
，若
，则
13．
则
1
14、函数f(x)为R上的奇函数，且当x<0时 ,
f(x) =x(x－1) , 则当x>0时, f(x)= －x（x+1）
三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.
15．(本题满分13分)
计算: （1）
（2）
÷
解：（1）原式= log2(log33) 2分
=log21 4分
=0 6分
（2）原式=
11分
= 4a 13分
16．(本题满分13分)
已知
，且A∩B=B，求
的值。
解：∵A∩B=B ∴
4分
即
7分
当
时，
，
符合题意；
8分
当
时，
符合题意；
9分
当
时，
，由元素的互异性，不符合题意故舍去。
11分
故x=0或x=2。 13分
17. (本题满分13分)
已知函数
，求
，
，
，
的值。
解： 
=6+
+2=8+ 3分
=
6分
=
9分
=
13分
18. (本题满分13分)
求不等式 
中的x的取值范围.
解: 对于 ，
当 
时，有 10x+23 > 27x-28 ,
5分
解得 x＜3 ； 6分
当 
时，有 10x+23 < 27x-28 ,
10分
解得 x＞3 . 11分
所以，当 时，x的取值范围为{x︱x＜3}；
当时，x的取值范围为{x︱x＞3}.
13分
19.（本小题满分14分）
已知函数f (x)=x 2+ax+b，且对任意的实数x都有f (1+x)=f (1－x) 成立.
（1）求实数 a的值；
（2）利用单调性的定义证明函数f(x)在区间[1，＋∞
上是增函数.
解：（1）由f (1+x)=f (1－x)得，
(1＋x)2＋a(1＋x)＋b＝(1－x)2＋a(1－x)＋b， 3分
整理得：(a＋2)x＝0， 5分
由于对任意的x都成立，∴ a＝－2. 7分
（2）根据（1）可知 f ( x )=x 2－2x+b，下面证明函数f(x)在区间[1，＋∞上是增函数.
设
，则
＝（
）－（
） 9分
＝（
）－2（
）
＝（）（
－2）
11分
∵，则＞0，且－2＞2－2＝0，
12分
∴ ＞0，即
，
13分
故函数f(x)在区间[1，＋∞上是增函数.
14分
20．(本题满分14分)
已知：函数
对一切实数
都有
成立，且
.
（1）求
的值。
（2）求的解析式。
（3）已知
，设P：当
时，不等式
恒成立；Q：当
时，
是单调函数。如果满足P成立的
的集合记为
，满足Q成立的的
集合记为
，求∩
（
为全集）。
解：（1）令
，则由已知
∴
4分
（2）令
， 则
又∵
∴
8分
（3）不等式 即
即
当时，
， 又
恒成立
故
10分
又
在
上是单调函数，故有
∴
12分
∴∩=
14分