高一数学必修4第一章任意角的三角函数测试题
班级 座号 姓名
（考试时间：90分钟）
一. 选择题 （每小题3分，共30分）
1. 与-463
角终边相同的角为（ ）
A． K
360+463， K
Z B. K 360+103， KZ
C
. K 360+257， KZ
D. K 360-257， KZ
2. sin(-
)的值是（ ）
A. 
B. - C. 
D.
-
3. 设角α是第二象限角，且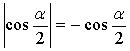
，则
是（ ）
A．第一象限角 B．第二象限角
C．第三象限角 D．第四象限角
4. 下列函数中属于奇函数的是（ ）
A.y
= sinx + 1
B. y = cos(x + 
)
C.
y = sin(x - )
D. y =
cosx - 1
5. 函数y=cosx（x [o ,2
]）的图象与直线 y = 1 所围成的图形的面积为（ ）
A. 
B. 
C. 
D. 
6. 函数y = 2sin (2x +
)的一条对称轴是（ ）
A. x = 
B. x = C. x = D. x = 
7. 函数y = 2sin (
)的单调递增区间是（ ）
A. [
] （kZ）
B. [
] （kZ）
C . [
] （kZ）
D. [
] （kZ）
8.
函数y = 
的值域是( )
A. { 0 } B. [ -2 , 2 ] C. [ 0 , 2 ] D.[ -2 , 0 ]
9.
当
为第二象限角时，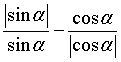
的值是（
）
A. 1 B. 0 C. 2 D. -2
10.
已知sincos
,且
，则sin+cos的值为（ ）
A. 
B. -
C. 
D.
二. 填空题 （每小题4分，共16分）
1.已知 tan=2,则sin
+sincos=
2. 函数y =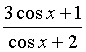 
的值域是
3. 求使sin >的的取值范围是
4.已知E={θcosθ<sinθ，0≤θ≤2π}，F={θtanθ<sinθ}.则E∩F=
三. 解答题(5个小题，共54分)
1. 已知
, 求
、
的值。 （8分）
2. 化简：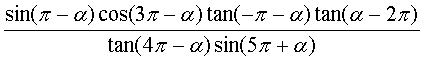
（8分）
3. 已知一个半径r为的扇形，它的周长等于弧所在的圆的半周长，求这个扇形的圆心角和面积。（10分）
3.
若函数y = a – bsinx的最大值为
,最小值为
,求函数
y=- 4sinbx的最值和最小正周期。 （14分）
4.
(1) 作函数y = 2 sin ( 2x + )的简图； （2）指出该函数的对称中心的坐标； （3）指出该函数的图象是由函数的图象经过怎样的变化而得到的。（14分）
第一章任意角的三角函数测试题答案
一. 选择题
C ADBDBBDCA
二. 填空题
1.
2. [
]
3. （
）
4. （
）
三. 解答题
1. 提示：（1）当是第三象限角，则
（2）当是第四象限角，则
2. 提示： 化简结果为
3. 提示： 
4. 提示：（1）当
时，由题意得：a + b=
, a - b=
解得：a= b=1
函数y= - 2sinx
此时最大值为2，最小值为-2，最小正周期为2
（2） 当
时，由题意得：a - b= , a + b= 解得：a= b= -1
函数y=2sinx
此时最大值为2，最小值为-2，最小正周期为2
综上所述，函数y=-4asinbx的最大值为2，最小值为-2，最小正周期为2
5. （1）图象（略）
（2）对称中心为（
）
（3）（略）