(数学3必修)第一章 算法初步
[综合训练B组]
一、选择题
1![]() 用“辗转相除法”求得
用“辗转相除法”求得![]() 和
和![]() 的最大公约数是( )
的最大公约数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
2![]() 当
当![]() 时,下面的程序段结果是 ( )
时,下面的程序段结果是 ( )
|
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
3![]() 利用“直接插入排序法”给
利用“直接插入排序法”给![]() 按从大到小的顺序排序,
按从大到小的顺序排序,
当插入第四个数![]() 时,实际是插入哪两个数之间
( )
时,实际是插入哪两个数之间
( )
A![]()
![]() 与
与![]() B
B![]()
![]() 与
与![]() C
C![]()
![]() 与
与![]() D
D![]()
![]() 与
与![]()
4![]() 对赋值语句的描述正确的是
( )
对赋值语句的描述正确的是
( )
①可以给变量提供初值 ②将表达式的值赋给变量
③可以给一个变量重复赋值 ④不能给同一变量重复赋值
A![]() ①②③ B
①②③ B![]() ①②
C
①②
C![]() ②③④
D
②③④
D![]() ①②④
①②④
5![]() 在repeat 语句的一般形式中有“until A”,其中A是 ( )
在repeat 语句的一般形式中有“until A”,其中A是 ( )
A![]() 循环变量 B
循环变量 B![]() 循环体 C
循环体 C![]() 终止条件 D
终止条件 D![]() 终止条件为真
终止条件为真
6![]() 用冒泡排序法从小到大排列数据
用冒泡排序法从小到大排列数据 ![]()
需要经过( )趟排序才能完成![]()
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
二、填空题
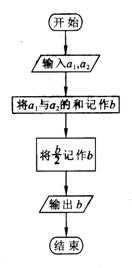
1![]() 根据条件把流程图补充完整,求
根据条件把流程图补充完整,求![]() 内所有奇数的和;
内所有奇数的和;
(1) 处填
(2) 处填
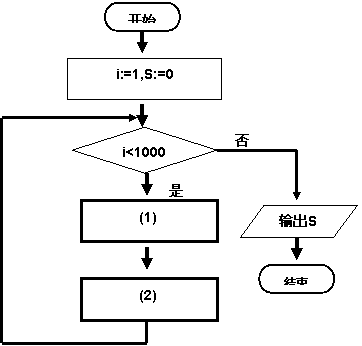
2![]() 图中所示的是一个算法的流程图,已知
图中所示的是一个算法的流程图,已知![]() ,输出的
,输出的![]() ,则
,则![]() 的值是____________
的值是____________![]()
3![]() 下列各数
下列各数![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 中最小的数是____________
中最小的数是____________![]()
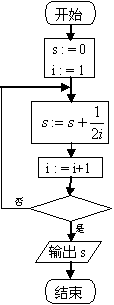 4
4![]() 右图给出的是计算
右图给出的是计算![]() 的值的一个流程图,其中判断
的值的一个流程图,其中判断
框内应填入的条件是____________![]()
5![]() 用直接插入排序时对:
用直接插入排序时对:![]() 进行从小到大排序时,第四步
进行从小到大排序时,第四步
得到的一组数为:
___________________________________![]()
三、解答题
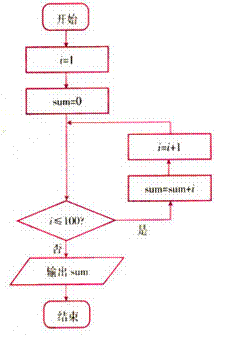
1![]() 以下是计算
以下是计算![]() 程序框图,请写出对应的程序
程序框图,请写出对应的程序![]()
2![]() 函数
函数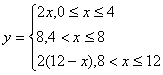 ,写出求函数的函数值的程序
,写出求函数的函数值的程序![]()
3![]() 用辗转相除法或者更相减损术求三个数
用辗转相除法或者更相减损术求三个数![]() 的最大公约数
的最大公约数![]()
4![]() 意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔
意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔![]() 问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序
问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序![]()
数学3(必修)第一章 算法初步 [综合训练B组]
参考答案
一、选择题
1![]() D
D
![]()
![]() 是
是![]() 和
和![]() 的最大公约数,也就是
的最大公约数,也就是![]() 和
和![]() 的最大公约数
的最大公约数
2![]() C
C
![]()
3![]() B
先比较
B
先比较![]() 与
与![]() ,得
,得![]() ;把
;把![]() 插入到
插入到![]() ,得
,得![]() ;把
;把![]() 插入到
插入到![]() ,得
,得![]() ;
;
4![]() A
见课本赋值语句相关部分
A
见课本赋值语句相关部分
5![]() D
Until标志着直到型循环,直到终止条件成就为止
D
Until标志着直到型循环,直到终止条件成就为止
6![]() B
经过第一趟得
B
经过第一趟得![]() ;经过第二趟得
;经过第二趟得![]() ;经过第三趟得
;经过第三趟得
![]() ;经过第四趟得
;经过第四趟得![]() ;经过第五趟得
;经过第五趟得![]() ;
;
二、填空题
1![]() (1)
(1)![]() (2)
(2)![]()
2![]()
![]()
![]()
3![]()
![]()
![]() 、
、 ![]() 、
、
![]() 、
、 ![]()
4![]()
![]()
5![]()
![]()
![]() ①;
①; ![]() ②;
②;
![]() ③;
③;![]() ④
④
三、解答题
1![]() 解: i=1
解: i=1
sum=0
WHILE i<=100
sum=sum+i
i=i+1
WEND
PRINT sum
END
2![]() 解:INPUT “x=”;x
解:INPUT “x=”;x
IF x>=0 and x<=4 THEN
y=2![]() x
x
ELSE IF x<=8 THEN
y=8
ELSE y=2*(12-x)
END IF
END IF
PRINT y
END
3![]() 解: 324=243×1+81
解: 324=243×1+81
243=81×3+0
则 324与 243的最大公约数为 81
又 135=81×1+54
81=54×1+27
54=27×2+0
则 81 与 135的最大公约数为27
所以,三个数 324、243、135的最大公约数为 27![]()
另法![]()
![]()
![]() 为所求
为所求![]()
4![]() 解: 根据题意可知,第一个月有
解: 根据题意可知,第一个月有![]() 对小兔,第二个月有
对小兔,第二个月有![]() 对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第
对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第![]() 个月有
个月有![]() 对兔子,第
对兔子,第![]() 个月有
个月有![]() 对兔子,第
对兔子,第![]() 个月有
个月有![]() 对兔子,则有
对兔子,则有![]() ,一个月后,即第
,一个月后,即第![]() 个月时,式中变量
个月时,式中变量![]() 的新值应变第
的新值应变第![]() 个月兔子的对数(
个月兔子的对数(![]() 的旧值),变量
的旧值),变量![]() 的新值应变为第
的新值应变为第![]() 个月兔子的对数(
个月兔子的对数(![]() 的旧值),这样,用
的旧值),这样,用![]() 求出变量
求出变量![]() 的新值就是
的新值就是![]() 个月兔子的数,依此类推,可以得到一个数序列,数序列的第
个月兔子的数,依此类推,可以得到一个数序列,数序列的第![]() 项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为
项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为![]() ,以此为基准,构造一个循环程序,让表示“第×个月的
,以此为基准,构造一个循环程序,让表示“第×个月的![]() 从
从![]() 逐次增加
逐次增加![]() ,一直变化到
,一直变化到![]() ,最后一次循环得到的
,最后一次循环得到的![]() 就是所求结果
就是所求结果![]() 流程图和程序如下:
流程图和程序如下:
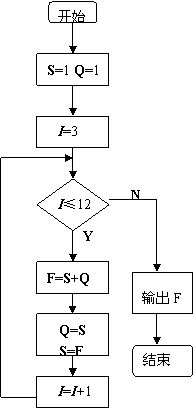 | |||
| |||