高一数学算法初步试题

高一数学算法初步试题

一.　 选择题: (每小题5分,共60分)

1. 算法的三种基本结构是 (　　)

  A. 顺序结构、模块结构、条件结构　　　 B. 顺序结构、循环结构、模块结构

  C. 顺序结构、条件结构、循环结构　　　 D. 模块结构、条件结构、循环结构

2. 将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 (　　)

a=c c=b b=a

b=a a=b

c=b b=a a=c

a=b b=a

　A.　　　　　　 B.　　　　　　　  C.　　　　　　　　 D.

3. 给出以下四个问题,①输入一个数x,输出它的相反数.②求面积为6的正方形的周长.

③求三个数a,b,c中的最大数.④求函数的函数值.　其中不需要用条件语句来描述其算法的有 (　　)

A. 1个　　　　　 B. 2个　　　　C. 3个　　　　 D. 4个

4. 下面为一个求20个数的平均数的程序,在横线上应填充的语句为 (　　)

	S=0 i=1 DO  INPUT　x  S=S+x  i=i+1 LOOP UNTIL　_____ a=S/20 PRINT　a END

A.  i>20

 B.  i<20

C.  i>=20

D.　　　　 i<=20

5.若在区间内单调,且,则在区间内 (　　)

　A. 至多有一个根　　 B. 至少有一个根　　 C. 恰好有一个根　　 D. 不确定

6. 将389 化成四进位制数的末位是 (　　)

　A. 1　　　　　　　  B. 2　　　　　　  C. 3　　　　　  D. 0

7. 下列各数中最小的数是 (　　)

　A.　　　　 B.　　　　 C.　　　　 D.

8. 用秦九韶算法计算多项式当时的值时,需要做乘法和加法的次数分别是 (　　)

　A. 6 , 6　　　　　 B. 5 , 6　　　　  C. 5 , 5　　　 D. 6 , 5

9. 用秦九韶算法计算多项式在时的值时,的值为 (　　)

　A. －845　　　　　  B. 220　　　　  C. －57　　　　 D. 34

10. 用冒泡法对一组数: 37,21,3,56,9,7进行排序时,经过多少趟排序后,得到一组数:

　 3,9,7,21,37,56.　(　　)

　A.  2　　　　　 B.　3　　　　　  C.　4　　　　　　 D. 5

11. 下左程序运行后输出的结果为  (　　 )

　A. 50　　　　　  B. 5　　　　　  C. 25　　　　　  D. 0

	a=0 j=1 WHILE　j<=5   a=(a+j) MOD 5   j=j+1 WEND PRINT　a END 第11题		x=1 y=1 WHILE　 x<=4 Z=0 WHILE　y<=x+2 　 Z=Z+1 　 y=y+1 WEND PRINT　Z x=x+1 y=1 WEND END 　　 第12题

12. 上右程序运行后输出的结果为 (　　 )

　 A. 3　4  5　6　　　B. 4　5  6　7　　　 C. 5  6  7　8　　 D. 6　7  8　9

二.　 填空题.(每小题4分,共16分)

13. 已知点A(-1,0),B(3,2),则线段AB的垂直平分线的方程为_____________________.

14. 用直接插入排序时对:7,1,3,12,8,4,9,10进行从小到大排序时,第四步得到的一组数

为: ___________________________________.

15. 下左程序运行后输出的结果为_________________________.

	x=5 y=－20 IF  x<0　THEN 　 x=y－3 ELSE 　 y=y+3 END IF PRINT　x－y ； y－x END 　 第15题		j=1 n=0 WHILE　j<=11 　 j=j+1 　 IF　j MOD 4=0　THEN 　　 n=n+1 　 END IF 　 j=j+1 WEND PRINT　n END 　　　　　 第16题

16.上右程序输出的n的值是_____________________.

三.　 解答题: (6小题,共74分.注意:解答题必须要写出必要的文字说明或步骤)

17. (12分)

用辗转相除法或者更相减损术求三个数 324 , 243 , 135 的最大公约数.

 

18. (12分)

　设计一个计算1+2+3+…+100的值的算法,并画出相应的程序框图.(要求用循环结构)

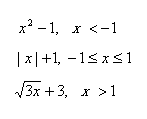19. (12分)

已知函数　 y  ={　　　　　　　　　　 , 编写一程序求函数值.

20.　 (12分)

　　某车间生产某种产品，固定成本为2万元，每生产一件产品成本增加100元，已知总收益R(总收益指工厂出售产品的全部收入，它是成本与总利润的和，单位：元)是年产量Q(单位：件)的函数，并且满足下面关系式：

R=f(Q)=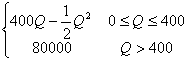，求每年生产多少产品时，总利润最大？此时总利润是多少元？

21.　(12分)

　　已知函数对任意实数都有，且当时，

，求在上的值域。

22.　(14分)

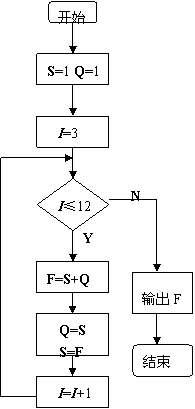
意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序.

高一下学期第一次月考数学试题答案

一.　 选择题: C B B A C　 A D A C B　 D A

二.　 填空题:

13: 　 14: [ 1　3  7　12 ] 8　4　9  10　 15: 22　－22　 16:  3

三.　 解答题:

17. 解:　　324=243×1＋81　　

243=81×3＋0　　

则 324与 243的最大公约数为 81

　　　　又 135=81×1＋54　　

 81=54×1＋27　　　

54=27×2＋0

　　　　则 81 与 135的最大公约数为27

　所以,三个数 324、243、135的最大公约数为 27.

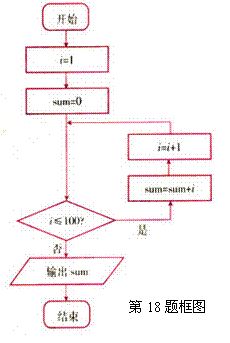
18. 解:第一步:设i的值为1;

　　　 第二步:设sum的值为0;

　　　 第三步:如果i≤100执行第四步,

否则转去执行第七步;

　　　 第四步:计算sum＋i并将结果代替sum;

　　　 第五步:计算i＋1并将结果代替i;

　　　 第六步:转去执行第三步;

　　　 第七步:输出sum的值并结束算法.

INPUT　“x=” ; x IF  x<－1　THEN y=x^2-1 ELSE IF　x>1　THEN 　　y=SQR(3*x)+3 ELSE 　　y=ABS(x)+1 END IF END IF PRINT　“y=” ; y END 　　 第19题

19. 解:

20. 解: y=R－100Q－20000=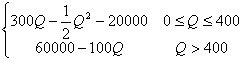(Q∈Z),每年生产300件时利润最大，最大值为25000元。

21.解: 设　且，则，

　　由条件当时，　

　　又 为增函数，

　　令，则　 又令　　得

　　，　故为奇函数，

　　，

　　上的值域为

S=1 Q=1 I=3 WHILE　I<=12 　 F=S+Q 　 Q=S 　 S=F 　 I=I+1 WEND PRINT　F END

22.解: 分析: 根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N个月有两F对兔子,第N－1个月有S对兔子,第N－2个月有Q对兔子,则有F=S+Q,一个月后,即第N+1个月时,式中变量S的新值应变第N个月兔子的对数(F的旧值),变量Q的新值应变为第N－1个月兔子的对数(S的旧值),这样,用S+Q求出变量F的新值就是N+1个月兔子的数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第×个月的I从3逐次增加1,一直变化到12,最后一次循环得到的F”就是所求结果. 流程图和程序如下: