高一数学复习——解三角形
班级 姓名 学号
一．复习要点
1．正弦定理:
或变形：
.
2．余弦定理：
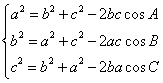或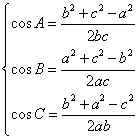 
.
3．（1）两类正弦定理解三角形的问题：1、已知两角和任意一边，求其他的两边及一角.
2、已知两角和其中一边的对角，求其他边角.
（2）两类余弦定理解三角形的问题：1、已知三边求三角.
2、已知两边和他们的夹角，求第三边和其他两角.
4．判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式.
5．解题中利用
中
，以及由此推得的一些基本关系式进行三角变换的运算，如：
.
6．求解三角形应用题的一般步骤：
（1）分析：分析题意，弄清已知和所求；
（2）建模：将实际问题转化为数学问题，写出已知与所求，并画出示意图；
（3）求解：正确运用正、余弦定理求解；
（4）检验：检验上述所求是否符合实际意义。
二．例题分析
例1、在
中，已知
，求
。
例2、在四边形
中，
，
，
，求四边形的面积
。
例3、在中，已知
，试判断的形状
例4、隔河看两目标
和
，但不能到达，在岸边选取相距
km的
和
两点，同时，测得
，
，
，
（
在同一个平面），求两目标
之间的距离。
三．巩固练习
1、在锐角中，若
，则
的范围
（ ）
（A）
（B） 
（C） 
（D） 
2、在中，若面积
，则
等于
（ ）
（A）
（B） 
（C） 
（D） 
3、的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且
，则
________
4、设是中的最小角，且
，则
的取值范围是__________
5、在中，如果
则
_________
6、在中，角
对应的边分别是
，若
，求
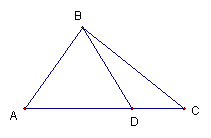7、如图一个三角形的绿地
，
边长7米，由点看的张角为
，在
边上一点处看得张角为
，且
，试求这块绿地得面积。
8、在中分别为
的对边，若
，
（1）求的大小；（2）若
，求
和
的值。
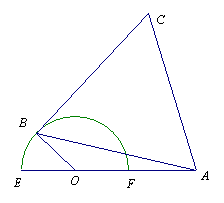9、图，
，是半个单位圆上的动点，是等边三角形，求当
等于多少时，四边形
的面积最大，并求四边形面积的最大值．
答案：
例1．
例2．
例3．等腰三角形或直角三角形
例4．
巩固练习：
1．
2．
3． 
4． 
5． 
6． 
7． 
8． （1）
（2）
9．当
时，
的最大值为