高一数学竞赛试题

高一数学竞赛试题

一、选择题(每小题5分, 共40分, 每题仅有一个正确答案)

1.已知函数f(x)满足f()=log₂, 则f(x)的解析式是(　　)

　A.2^-x　　B.log₂ x　　　C. -log₂ x　　　D.x^-2

2.已知f(x)=1-(-1≤x≤0), 函数y=f(x+1)与y=f(3-x)的图象关于直线l 对称,

则直线l的方程为(　　)

A.x=2　　 B.x=1　　 C.x=　　 D.x=0

3.设f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f()=0, f(log₄x)＞0, 那么x的

取值范围是(　　)

　A.x＞2或＜x＜1　　 B.x＞2　　 C.＜x＜1　　 D.＜x＜2

4.已知定义域为R的函数y=f(x)在(0, 4)上是减函数, 又y=f(x+4)是偶函数, 则(　　)

　A. f(5)＜f(2)＜f(7)　　　B. f(2)＜f(5)＜f(7)

　C. f(7)＜f(2)＜f(5)　　　D. f(7)＜f(5)＜f(2)

5.若不等式2x²+ax+2≥0对一切x∈(0,]成立, 则a的最小值为(　　)

　A.0　　 B. -4　　  C.-5　　 D. -6

6.已知定义域为R的函数f(x)满足f(-x)= -f(x+2), 且当x＞1时, f(x)单调递增.

如果x₁+x₂＜2, 且(x₁-1)(x₂-1)＜0, 则f(x₁)+f(x₂)的值(　　)

　A.恒大于0　　B.恒小于0　　C.可能为0　　D.可正可负

7.若函数f(x)=25^-x+5 -4×5^-x+5 +m的图象与x轴有交点, 则实数m的取值范围是(　　)

  A.m＞0　　 B.m≤4　　 C.0＜m≤4　　D.0＜m≤3

8.对定义在区间[a, b]上的函数f(x), 若存在常数c, 对于任意的x₁∈[a, b]有唯一的x₂∈[a, b], 使得=c成立, 则称函数f(x)在区间[a, b]上的“均值”为c. 那么,

函数f(x)=lgx在[10, 100]上的“均值”为(　　)

　A.　　 B.10　　 C.　　 D.
二、填空题(每小题5分, 共30分)

9.已知集合A={x 4-2k＜x＜2k-8}, B={x -k＜x＜k},

若A (≠B, 则实数k的取值范围是____________________

10.若函数y=log_a(2x²+ax+2)没有最小值, 则a的所有值的集合是_________________

11.集合P={xx=2ⁿ-2^k, 其中n, k∈N, 且n＞k},　Q={x1912≤x≤2006, 且x∈N},

那么, 集合P∩Q中所有元素的和等于_________

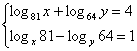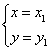12.已知方程组的解为和,

则log₁₈(x₁ x₂ y₁ y₂)=________

13.若关于x的方程4^x+2^xm +5=0至少有一个实根在区间[1, 2]内,

则实数m的取值范围是_________________

14.设card(P)表示有限集合P的元素的个数. 设a=card(A), b=card(B), c=card(A∩B),

且满足a≠b, (a+1)(b+1)=2006,　2^a+2^b=2^a+b-c+2^c, 则max{a, b}的最小值是______

三、解答题(每题10分, 共30分)

15.设函数f(x)=x+1+ax+1.

(1)当a=2时, 求f(x)的最小值;

(2)若f(-1)=f(1), f(-)=f()(a∈R, 且a≠1), 求a的值

16.设函数f(x)的定义域是(0, +∞), 且对任意的正实数x, y都有f(xy)=f(x)+f(y)恒成立.

已知f(2)=1, 且x＞1时, f(x)＞0.

(1)求f()的值;　 (2)判断y=f(x)在(0, +∞)上的单调性, 并给出你的证明;

　(3)解不等式f(x²)＞f(8x-6) -1.

17.已知函数f(x)=log_a (ax²-x+)在[1, 2]上恒为正数, 求实数a的取值范围.

(洪一平命题,　后附参考答案)

参考答案

1.C　　2.B　　3.A 　 4.A　　5.C　　6.B　　7.D　　8.D

9.(0, 4]　　 10.(0,1)∪[4,+∞)　　　　  11.3904

12. 12　　　　13.　　　　 14.58

15.(1)当a=2时, f(x)=x+1+2x+1=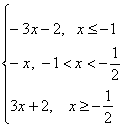

  ∴当x≤-1时, f(x)递减, 故f(x)≥f(-1)=1, 当-1＜x＜-时, f(x)递减, 故f(x)＞f(-)=,

　当x≥-时, f(x)递增, 故f(x)≥f(-)=, 因此, f(x)的最小值为

  (2)由f(-1)=f(1)得 2+a+1=1-a  (*),　两边平方后整理得a+1= -(a+1)

　 ∴ a≤-1　  ①

同理, 由f(-)=f()得2++1=1-,　对比(*)式可得

　 ≤-1 ∴ -1≤a＜0　　 ②

　 由①②得a= -1

16.(1)令x=y=1, 则可得f(1)=0, 再令x=2, y=, 得f(1)=f(2)+f(), 故f()= -1

  (2)设0＜x₁＜x₂, 则f(x₁) +f()=f(x₂) 即f(x₂) -f(x₁)=f(),

∵＞1, 故f()＞0, 即f(x₂)＞f(x₁) 故f(x)在(0, +∞)上为增函数

  (3)由f(x²)＞f(8x-6) -1得f(x²)＞f(8x-6) +f()=f [(8x-6)],

　　故得x²＞4x-3且8x-6＞0, 解得解集为{x＜x＜1或x＞3}

17.题设条件等价于(1) 当a＞1时, ax²-x+＞1对x∈[1, 2]恒成立;　(2)当0＜a＜1时,

0＜ax²-x+＜1对x∈[1, 2]恒成立.

由(1)得a＞对x∈[1, 2]恒成立, 故得a＞.

由(2)得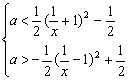 对x∈[1, 2]恒成立, 故得＜a＜.

　因此, a的取值范围是a＞或＜a＜